Kezdőlap


Feladat:	1039. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bach Katalin , Bencsik I. , Biborka T. , Bollobás Béla , Csikor F. , Csizy László , Dömötör Gy. , Fábián G. , Fejes L. , Fekete J. , Frint G. , Fritz J. , Gagyi-Pálffy A. , Gálfi l. , Grüner Gy. , Hahn J. , Hajna J. , Homitzky L. , Kardeván P. , Knuth E. , Kóta G. , Kóta J. , Krámli A. , Máté A. , Miklóssy E. , Molnár E. , Nagy Dezső , Nagypál B. , Opálény M. , Pósch Margit , Rátkai J. , Székely J. , Vámos P. , Várady G. , Vesztergombi Gy.
Füzet:	1961/április, 151 - 154. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1960/április: 1039. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A $P F_{1} F_{2}$ háromszög $F_{1} F_{2}$ oldala állandó ‐ a szokásos jelöléssel $2 c$ ‐, $P F_{1}$ és $P F_{2}$ pedig a $P$ pont két vezérsugara: $r_{1}$ , $r_{2}$ , amelyekre $r_{1} + r_{2} = 2 a$ . Így a háromszög kerülete $2 (a + c)$ , tehát a félszög tangensének az oldalakkal való kifejezéseivel

\begin{matrix} tg φ_{1} = \sqrt[]{\frac{(a + c - 2 c) (a + c - r_{1})}{(a + c) (a + c - r_{2})}}, tg φ_{2} = \sqrt[]{\frac{(a + c - 2 c) (a + c - r_{2})}{(a + c) (a + c - r_{1})}}, \end{matrix}

így pedig szorzatuk

\begin{matrix} tg φ_{1} \cdot tg φ_{2} = \frac{a - c}{a + c}, állandó . \end{matrix}

Csizy László (Pécs, Nagy Lajos g. III. o. t.)

II. megoldás: Tekintsük adottnak az ellipszist az

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{matrix}

(1)

egyenlettel, ahol az

a^{2} > b^{2}

. Így a fókuszok koordinátái:

F_{1} (- c, 0)

F_{2} (c, 0)

, ahol

\begin{matrix} c = \sqrt[]{a^{2} - b^{2}} . \end{matrix}

(2)

Az ellipszis szimmetriája alapján elég az állítást az olyan

P (x, y)

pontra belátnunk, melynek egyik koordinátája sem negatív:

x \geq 0

és

y > 0

(

y = 0

lehetőségét a feladat kizárta).
Legyen

P

két vezérsugara

P F_{1} = r_{1}

és

P F_{2} = r_{2}

P

vetülete az

X

-tengelyre

P'

, és messe a

2 φ_{1}

2 φ_{2}

szög felezője

P P'

-t

G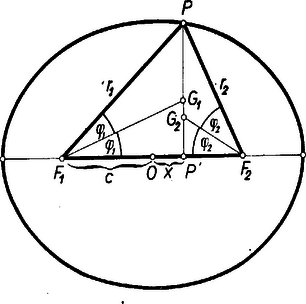_{1}

G_{2}

-ben.

Ekkor

\begin{matrix} tg φ_{1} = \frac{P' G_{1}}{F_{1} P'} = \frac{P' G_{1}}{c + x}, & (3) \\ tg φ_{2} = \frac{P' G_{2}}{F_{2} P'} = \frac{P' G_{2}}{c - x} . & (4) \end{matrix}

Alkalmazzuk a szögfelező osztási arányára vonatkozó tételt az

F_{1} P' P

és

F_{2} P' P

háromszögre:

\begin{matrix} \frac{G_{1} P}{P' G_{1}} = \frac{F_{1} P}{F_{1} P'} és \frac{G_{2} P}{P' G_{2}} = \frac{F_{2} P}{F_{2} P'}, \end{matrix}

azaz

\begin{matrix} \frac{y - P' G_{1}}{P' G_{1}} = \frac{r_{1}}{c + x} és \frac{y - P' G_{2}}{P' G_{2}} = \frac{r_{2}}{c - x} . \end{matrix}

Mindkét oldalhoz 1-et adva, majd a két tört egyenlőségének formájában írt aránypár belső tagjait felcserélve, végül (3)-at, (4)-et figyelembe véve

\begin{matrix} \frac{y}{P' G_{1}} = \frac{c + x + r_{1}}{c + x} és \frac{y}{P' G_{2}} = \frac{c - x + r_{2}}{c - x}, \\ tg φ_{1} = \frac{y}{c + x + r_{1}}, & (5) \\ tg φ_{2} = \frac{y}{c - x + r_{2}} . & (6) \end{matrix}

P P' F_{1}

derékszögű háromszögből (1) és (2) figyelembevételével

\begin{matrix} r_{1}^{2} = {(c + x)}^{2} + y^{2} = (a^{2} - b^{2}) + 2 c x + x^{2} + (b^{2} - \frac{b^{2} x^{2}}{a^{2}}) = a^{2} + 2 c x + \frac{c^{2} x^{2}}{a^{2}}, \end{matrix}

és így (mivel

x \geq 0

)

\begin{matrix} r_{1} = a + \frac{c x}{a} . \end{matrix}

Hasonlóan a

P P' F_{2}

háromszögből (

0 \leq x < a

és

c < a

folytán)

\begin{matrix} r_{2} = a - \frac{c x}{a} . \end{matrix}

Ezekkel (5) és (6) nevezője így írható:

\begin{matrix} c + x + r_{1} = c + x + a + \frac{c x}{a} = a + c + \frac{x}{a} (a + c) = (a + c) (1 + \frac{x}{a}), \\ c - x + r_{2} = c - x + a - \frac{c x}{a} = (a + c) (1 - \frac{x}{a}), \end{matrix}

tehát a kérdéses szorzat

\begin{matrix} tg φ_{1} \cdot tg φ_{2} = \frac{y}{(a + c) (1 + \frac{x}{a})} \cdot \frac{y}{(a + c) (1 - \frac{x}{a})} = \frac{y^{2}}{{(a + c)}^{2} (1 - \frac{x^{2}}{a^{2}})} = \\ = \frac{y^{2}}{{(a + c)}^{2} \frac{y^{2}}{b^{2}}} = \frac{b^{2}}{{(a + c)}^{2}} = \frac{a^{2} - c^{2}}{{(a + c)}^{2}} = \frac{a - c}{a + c}, állandó . \end{matrix}

Ezt kellett bizonyítanunk.
Meggondolásunk

x > c

esetén is érvényes, hacsak

P' G_{2}

-t előjellel együtt értjük. Így

2 φ_{2} > 90^{\circ}

és

F_{2} G_{2}

F_{2} P' P

háromszögben külső szögfelező, azonban a felhasznált tétel a külső szögfelezőre is érvényes.
Nem érvényes viszont vizsgálatunk az

x = c

esetre, mert ekkor

P' \equiv F_{2}

és az

F_{2} P' P

háromszög nem létezik. Ekkor

tg φ_{1}

értéke éppen a fent nyert állandó:

\begin{matrix} tg φ_{1} = \frac{y}{(a + c) (1 + \frac{c}{a})} = \frac{\frac{b}{a} \sqrt[]{a^{2} - c^{2}}}{\frac{{(a + c)}^{2}}{a}} = \frac{b^{2}}{{(a + c)}^{2}}, \end{matrix}

másrészt

2 φ_{2} = 90^{\circ}

, ezért

tg φ_{2} = 1

, tehát a szorzat értéke ugyanannyi, mint minden más esetben.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

Megjegyzés. Az állítás nem terjeszthető ki arra az esetre, ha

P

a nagytengely valamelyik végpontjában van, mert ekkor a

P F_{1} F_{2}

háromszög úgy fajul el, hogy

φ_{1}

és

φ_{2}

egyike

90^{\circ}

, és ezért a szorzatnak nincs értelme. ‐ Nincs értelme az állításnak körre sem, mert ott

F_{1}

és

F_{2}

egybeesnek,

φ_{1}

φ_{2}

határozatlanok.