Feladat: 1038. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bollobás B. ,  Csikor F. ,  Durst István ,  Farkas Z. ,  Frint G. ,  Fritz J. ,  Gagyi-Pálffy A. ,  Grüner Gy. ,  Knuth E. ,  Kóta Gábor ,  Marton D. ,  Máté A. ,  Máté E. ,  Máté Zs. ,  Molnár E. ,  Nagypál B. ,  Rátkai J. ,  Simonovits M. ,  Sonnevend Gy. ,  Várady G. 
Füzet: 1961/március, 120 - 122. oldal  PDF  |  MathML 
Témakör(ök): Gömb és részei, Térgeometriai számítások trigonometria nélkül, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1960/április: 1038. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: 1. Legyen az O középpontú k körbe írt négyzet ABCD (1. ábra), az AB, BC, CD oldal felező pontja rendre K, L, M, és az M-ből és K-ból L-en át húzott félegyenes messe 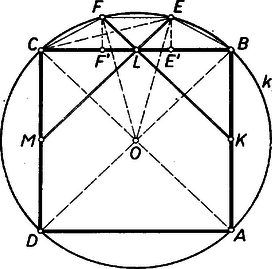k-t E, ill. F-ben.

 
 
1. ábra
 

Így ML a DBC háromszög középvonala, párhuzamos a DB átmérővel és merőlegesen felezi az OC sugarat. Ezért EC=EO=CO, az OCE háromszög egyenlő oldalú, és COE∢=60∘, tehát BOE∢=30∘. Hasonlóan BOF∢=60∘, COF∢=30∘, és így EOF∢=EOC∢-FOC∢=30∘=360∘/12. Eszerint az E, F pontok k-nak BC negyedívét három egyenlő részre osztják; ezzel az első állítást bebizonyítottuk.
 

2. Legyen az O középpontú g gömbbe írt ABCDA1B1C1D1 kocka (3. ábra) BCC1B1, ADD1A1 és ABCD lapjának középpontja rendre Q, R, S, és messe a Q-ból, ill. R-ből S-en át húzott félegyenes 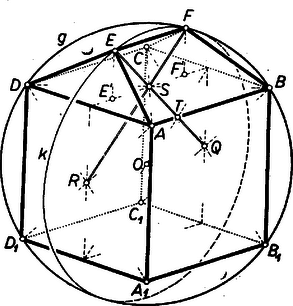g-t E, ill. F-ben.
 
 
3. ábra
 

Megmutatjuk, hogy az A, B, C, D, E, F csúcsokkal meghatározott konvex P* poliéder hasonló az 1958. évi Orsz. Középisk. Matematikai Tanulmányi Verseny II. fordulója 3. feladatában leírt1 és folytatólag a 951. feladatban2 vizsgált P poliéderhez. Ebből már következik az állítás, ugyanis az utóbbi feladatban (a III. megoldásban) bebizonyítottuk, hogy 1) P-t négyzetlapjánál fogva egy a élű kocka egy lapjára (kifelé) ráillesztve a négyzetlapjához nem tartozó 2 csúcsa ráesik a kocka köré írt gömbre, továbbá hogy 2) P-nek 6 példányát a kocka 1‐1 lapjára alkalmas állásban hasonlóan ráillesztve szabályos dodekaédert kapunk. E dodekaéder körülírt gömbje 1) szerint nyilván azonos a kocka körülírt gömbjével. ‐ Az 1) tényt így is kimondhatjuk: P bele van írva abba a gömbszeletbe, amelyet az a élű kocka köré írt gömbből a kocka egy lapsíkja lemetsz.
Mármost P*-ot ugyancsak a vizsgált kocka köré írt g-ből az ABCD lapsíkkal lemetszett gömbszeletben szerkesztettük, E és F csúcsai a BC él felező merőleges síkjában vannak és az AB él felező merőleges síkjára nyilvánvalóan szimmetrikusak. Ezért az említett hasonlósághoz elég azt megmutatni, hogy az EF él O-ból ugyanakkora szögben látható, mint P megfelelő éle a dodekaéder körülírt gömbjének középpontjából. Ha pedig mostani kockánk élét is a-nak vesszük, akkor azt elég belátnunk, hogy a kérdéses EF él hossza egyenlő P a-tól különböző éleinek idézett hosszával.
Messük kockánkat és g-t a QRS=φ síkkal. A metszet a oldalú négyzet (2. ábra), ill. egy k főkör, mert a sík nyilván átmegy 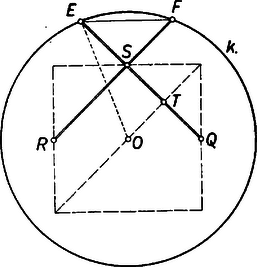O-n.
 
 
2. ábra
 

k-nak OE sugara egyenlő a kocka testátlójának felével, a3/2-vel. A metszetnégyzet középpontja ugyancsak O. EF-et az EFS háromszögből számítjuk, amely a szerkesztésnél fogva S-nél derékszögű és a szimmetria folytán egyenlő szárú. Legyen O vetülete QS-en T; ekkor OT=ST=a/8 (nyilván a metszetnégyzet átlójának 4-edrésze), ezért az EOT derékszögű háromszögből ET=a5/8, tehát ES=ET-ST=a(5-1)/8, végül EF=ES2=a(5-1)/2. Ezt akartuk bizonyítani.
 

Kóta Gábor (Tatabánya, Árpád g. III. o. t.)
 

II. megoldás: Legyenek az ABCD négyzet köré írt k kör BC negyedrészét 3 egyenlő részre osztó pontok E és F (1. ábra), a BC oldal középpontja L. Így BEFC nyilvánvalóan egy a k-ba írt szabályos 12-szög része, és elég megmutatnunk, hogy E-t és F-et a feladatban szereplő félegyenesek metszik ki. Ez pedig következik abból, ha bebizonyítjuk, hogy ELB∢=FLC∢=45∘. Mivel a BCFE négyszög szimmetrikus trapéz, elég az egyik szögről belátni, hogy 45∘-os.
Legyen E, F vetülete BC-n E', F'; nyilvánvalo, hogy E'F'=EF, és L felezi E'F'-t. Elég azt megmutatnunk, hogy az ELE' derékszögű háromszög egyenlő szárú. Mármost a kerületi szögek tétele szerint EBC∢=EBE'∢=30∘, ezért az EBE' derékszögű háromszögből EE'=BE/2=EF/2=E'F'/2=E'L. Ezt akartuk bizonyítani.
2. A második állítás helyett is hasonlóan elegendő a következőt bizonyítani: a g gömbbe írt szabályos dodekaéder E, F csúcsát az ABCD négyzet S középpontjával összekötő egyenes átmegy a BCC1B1, ADD1A1 négyzetek Q, R középpontján. Ehhez elég belátnunk, hogy a kérdéses egyenesek benne vannak a kocka BC élének φ felező merőleges síkjában, és az ABCD lappal 45∘-os szöget zárnak be.
Az I. megoldásban idézett eredmények szerint E, F valóban benne vannak φ-ben. Legyen E, F vetülete az ABCD lapon E', F', ekkor nyilván E'F'=EF és S felezi E'F'-t, és azt kell megmutatnunk, hogy az ESE' derékszögű háromszög egyenlő szárú. A kocka élét a-val, a dodekaéder élét b-vel jelölve E'S=b/2, az EE'=m szakaszra az idézett összefüggésekből
m2=a2-ab4=(ab+b2)-ab4=b24
és így m=b/2. Ezzel az állítást bebizonyítottuk.
 

Durst István (Szolnok, Verseghy F. g. IV. o. t.)

1Lásd a megoldást K. M. L. 17 (1958) 69‐71. o. ‐ P-nek 5 lapja, 6 csúcsa van, egy lapja a oldalú négyzet, összes többi élei egyenlők, közös b=a(5-1)/2 hosszukra ab+b2=a2, a négyzetlappal párhuzamos élének m magasságára pedig m2=a(a-b)/4. Továbbá P-nek két a négyzetlapra merőleges szimmetriasíkja van: a négyzet éleinek felező merőleges síkjai.

2Lásd a megoldást: K. M. L. 19 (1959) 178. o.