Kezdőlap


Feladat:	1036. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Biborka T. , Binder L. , Bollobás B. , Bónis Katalin , Csizy L. , Durst I. , Farkas Z. , Fejes L. , Frint G. , Gagyi Pálffy A. , Gáti P. , Grüner Gy. , Hahn J. , Hajna J. , Józsa S. , Kardeván P. , Katona Mária , Kóta G. , Kóta J. , Krámli A. , Meleghegyi László , Mocskónyi M. , Monár E. , Nováky A. , Pollai Marion , Rátkai J. , Sonnevend Gy. , Szarka Gy. , Tattay Emőke , Várady G.
Füzet:	1961/február, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai számítások trigonometria nélkül körökben, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1960/április: 1036. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott elrendezésben a ,,szomszédos'' gyűrűk átfedik egymást, vagyis azok, melyeknek középpontjai az említett egyenlő szárú derékszögű háromszögek egy-egy befogójának végpontjai (1. ábra).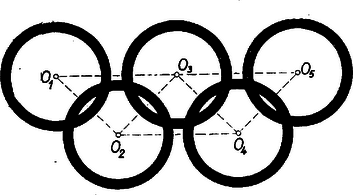

1. ábra

Éspedig szomszédos gyűrűk külső és belső határoló körei közül bármelyik kettő metszi egymást, mert középpontjaik távolsága

d = 24 / \sqrt[]{2} = 12 \sqrt[]{2} < 17

‐ ugyanis négyzeteikre

288 < 289

, és ez kisebb a belső sugarak

9 + 9 = 18

összegénél, másrészt nagyobb a külső és a belső sugár különbségénél,

2

-nél. ‐ Ezzel szemben két olyan gyűrűnek, melyek középpontja egy egyenlő szárú derékszögű háromszög átfogójának két végpontja, nincs közös része, mert még a külső határoló körök sugarának

11 + 11 = 22

összege is kisebb az átfogónál.
Bármelyik két szomszédos gyűrűnek két közösen átfedett része van, a szomszédos gyűrű párok száma

4

, így a kétszer átfedett részek száma a jelvényben

8

, nyilvánvalóan valamennyi egybevágó. Egy közös rész területét

t_{2}

-vel, egy gyűrűét pedig

t_{1}

-gyel jelölve az

5

gyűrű által lefedett terület

5 t_{1} - 8 t_{2}

, mert az

5 t_{1}

tagban mindegyik közös részt

2

-szer számítottuk be.
Legyen a gyűrűk határoló köreinek sugara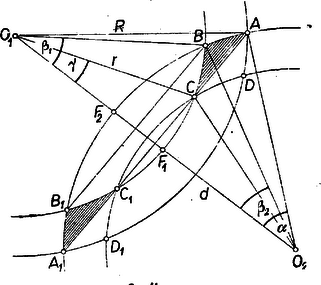

R

és

r

, ahol

R > r

. Így

t_{1} = (R^{2} - r^{2}) π

2. ábra

Legyen két szomszédos gyűrű középpontja

O_{1}

O_{2}

(2. ábra), és egyik közös részük az

A B C D

görbevonalú négyszög, ahol

A

a két nagyobb és

C

a két kisebb kör metszéspontja ‐ ezek

O_{1} O_{2}

felező merőlegesének pontjai ‐,

B

pedig az

O_{1}

-höz közelebbi csúcs, legyen továbbá

A B C D

tükörképe

O_{1} O_{2}

-re ‐ e két gyűrű másik közös része ‐

A_{1} B_{1} C_{1} D_{1}

. A szimmetria folytán a közös rész területe egyenlő az

A B C

és

A_{1} B_{1} C_{1}

vegyes határvonalú háromszögek területének összegével. Ezt megkaphatjuk pl. Az

A B B_{1} A_{1}

és

B C C_{1} B_{1}

vegyes vonalú négyszögek (görbeszárú trapéznak területfenék különbségeként, végül az utóbbiak mindegyike két körszelet területének különbsége. Éspedig ─ ha az

O_{1}

középpontú

C C_{1}

ív és az

O_{2}

középpontú

A A_{1}

ív felezőpontja

F_{1}

, ill.

F_{2}

, továbbá az idomok területét ugyanúgy jelölve, mint magukat az idomokat ‐

\begin{matrix} t_{2} & = A B C + A_{1} B_{1} C_{1} = A B B_{1} A_{1} - B C C_{1} B_{1} = \\ = (A F_{2} A_{1} - B F_{2} B_{1}) - (B F_{1} B_{1} - C F_{1} C_{1}) . \end{matrix}

Az egymás utáni körszeletek

α

β_{2}

β_{1}

γ

fél nyílásszöge az

O_{1} O_{2} A

O_{1} O_{2} B

, ill.

O_{1} O_{2} C

háromszögből a

\begin{matrix} cos α = \frac{d}{2 R}, cos β_{2} = \frac{d^{2} + R^{2} - r^{2}}{2 d R}, \\ cos β_{1} = \frac{d^{2} + r^{2} - R^{2}}{2 d r}, cos γ = \frac{d}{2 r} \end{matrix}

összefüggésekkel kiszámítható, ezekből pedig a körszelet

t = ϱ^{2} (φ - sin φ) / 2

területképletével (ahol

ϱ

a sugár,

φ

a teljes nyílásszög ívmértékben):

\begin{matrix} t_{2} = \frac{R^{2}}{2} [(2 a - sin 2 a) - (2 β_{2} - sin 2 β_{2})] - \frac{r^{2}}{2} [(2 β_{1} - sin 2 β_{1}) - (2 γ - sin 2 γ)] . \end{matrix}

A számadatokkal

t_{1} = 40 π

;

\begin{matrix} α \approx 39, 52^{\circ} \approx 0, 6898, & β \approx 28, 54^{\circ} \approx 0, 4980, \\ β_{1} \approx 35, 72^{\circ} \approx 0, 6235; & γ \approx 19, 47^{\circ} \approx 0, 3397, \end{matrix}

így

t_{2} \approx 4, 54 {c m}^{2}

; végül a keresett terület

592, 0 {c m}^{2}

Meleghegyi László (Pécs, Nagy Lajos Gimn. III. o. t.)

Megjegyzés.

t_{2}

értékére tájékoztató becslést kapunk az

A B C D

deltoid területéből. A Pythagorász-tétel szerint

A A_{1} = 14 cm

C C_{1} = 6 cm

, így

A C = 4 cm

, másrészt

O_{1} B

-nek

O_{1} O_{2}

-n levő

31 \sqrt[]{2} / 6

hosszúságú vetületéből

B D = 5 \sqrt[]{2} / 3

, így a deltoid területe

10 \sqrt[]{2} / 3 \approx 4, 7 {c m}^{2}

. ‐ Másképpen,

A B C D

-t két irányban

R - r = 2 cm

magasságú paralelogrammával helyettesítve az adódik, hogy területe legalább

{(R - r)}^{2} = 4 {c m}^{2}

Tattay Emőke (Budapest, Kaffka Margit lg. III. o. t.)