Feladat: 1035. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Biborka T. ,  Bollobás B. ,  Csikor F. ,  Durst I. ,  Farkas Z. ,  Frint G. ,  Fritz J. ,  Gagyi Pálffy A. ,  Gálfi l. ,  Grüner Gy. ,  Hahn J. ,  Hajna J. ,  Kunszt Z. ,  Marton D. ,  Máté A. ,  Molnár E. ,  Nagypál B. ,  Pinkert A. ,  Pollai Marion ,  Szarka Gy. ,  Székely Jenő ,  Török Éva ,  Várady G. 
Füzet: 1961/április, 149 - 151. oldal  PDF  |  MathML 
Témakör(ök): Nomogramok, Feladat
Hivatkozás(ok):Feladatok: 1960/április: 1035. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az, hegy az x0 (valós) szám gyöke a p, q együtthatókhoz tartozó, a feladatban szereplő alakú egyenletnek, az azt jelenti, hogy teljesül

x02+px0+q=0.(1)

Ha az egyes egyenleteket egy derékszögű koordinátarendszerben a (p, q) ponttal ábrázoljuk, akkor ‐ az (1) egyenletben p-t és q-t változónak tekintve ‐ mindazokat az egyenleteket képviselő pontok, amely egyenleteknek az x0 gyöke, egy egyenest, a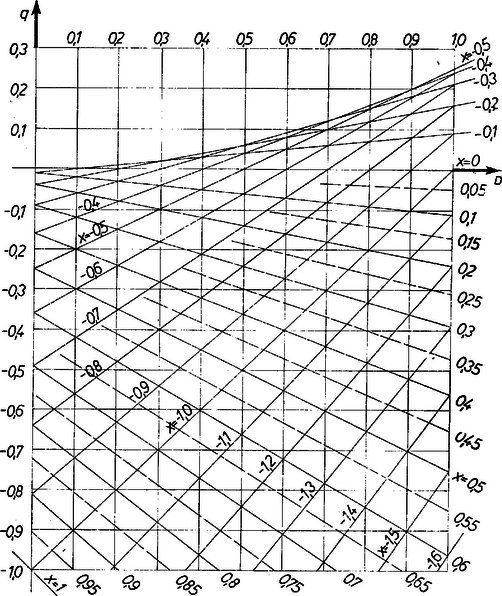
q=-x0p-x02
egyenlettel jellemzett e egyenest alkotják. Elvben az összes (x0 minden valós értékéhez tartozó) e egyenesek alkotják a szóban forgó nomogramot. Egy (p0, q0) ponton azon x értékekhez tartozó egyenesek mennek át, amely x értékek kielégítik a (p0, q0) ponttal ábrázolt egyenletet. Gyakorlatban korlátozzuk a (p, q) pontokat a sík egy véges részére a várható szükségletnek megfelelően (a gyakorlati alkalmazásokban ugyanis rendszerint csak bizonyos korlátok közötti (p, q) együtthatókra kell felkészülnünk); továbbá csak kiválogatott x értékekhez tartozó egyenesek egy‐egy szakaszát rajzoljuk meg úgy, hogy az egyenesek biztosan követhetők legyenek addig, ahol mellettük a megfelelő p, q, x érték félreérthetetlenül feltüntethető. Célszerű továbbá olyan utasítást adni ‐ amennyiben ez lehetséges ‐, amelynek alapján a nomogram használhatósági tartománya kiterjeszthető.
 
 

A sík p<0 félsíkján mellőzhetjük a nomogram elkészítését, mert p<0 esetén a g(x)≡x2+px+q=0 gyökei az f(x)≡x2-px+q=0 gyökeiből (-1)-gyel való szorzás útján megkaphatók. Ugyanis g(-x)≡f(x), tehát ha valamely x1-re f(x1)=0, akkor g(-x1)=0.
Az ábrán a sík p, q-koordinátarendszerének csak a 0≤p≤1, -1≤q≤0,25 téglalapját tüntettük fel, és ezen az x szám 0,1 n értékeihez tartozó e egyeneseket, ahol n egész szám. Téglalapunkon csak a -16≤n≤10 értékekhez tartozó egyeneseknek van pontjuk.
A nomogram használata általában egyezik a 963. feladatban látott nomograméval. Pl. az x2+0,5x-0,36=0 egyenlet gyökei x1=-0,9 és x2=0,4, mert a (0,5; -0,36) ponton két egyenes megy át és azokon az x=-0,9 és x=0,4 paraméter-érték van feltüntetve. Ha a (p, q) pont ,,közelében'' nem fekszik e egyenes, akkor az egyenletnek nincs valós gyöke. Ha a pont az ábra ,,üres'' és behálózott részének határán van, akkor vagy két egyenlő, vagy két majdnem egyenlő valós gyök van, vagy pedig olyan konjugált komplex gyökpár, amelyben a képzetes rész ,,kicsi''.
Ha |p| és q egyike vagy mindketteje kívül esik a figyelembe vett, fenti korlátokon, akkor keressük meg a legkisebb olyan pozitív egész α, ill. 2β kitevőt, amelyre már teljesül
|p|10α≤1,ill.-1≤q102β≤0,25,
majd α és β nagyobbikát γ-val jelölve alkalmazzuk az x2+px+q=0 egyenletre az x=10γz helyettesítést. Így z-re teljesülnie kell a
102γz2+10γpz+q=0,azazz2+p10γz+q102γ=0
egyenletnek, az utóbbi egyenlet gyökei pedig ábránkról leolvashatók, mert
|p10γ|=|p|10γ≤|p|10αés|q102γ|≤|q|102β.
Pl. az x2-25x-99,9=0 egyenlet esetében α=2 és β=1, mert 25/102=0,25≤1 és -1≤-99,9/102≤0,25, ennélfogva γ=2, és x=-102z-vel z2+0,25z-0,00999=0-hez leolvasható z1≈0,03 és z2≈-0,28, tehát x1≈-3, x2≈+28 (Számítással x1≈-3,504... és x2≈-28,504... adódik.)
Hasonlóan, ha p és q abszolút értékben közel járnak 0-hoz és a legnagyobb olyan pozitív egész δ, ε, amellyel még fennáll
10δ|p|≤1,ill.-1≤102εq≤0,25,
akkor δ és ε kisebbikét η-val jelölve x=z/10η helyettesítéssel olyan egyenletet kapunk, amelynek gyökei a nomogramról pontosabban olvashatók le, mint az eredeti egyenletéi, mert így várható, hogy a (p, q) pont körül a ,,szomszédos'' e egyenesek távolsága nagyobb.
x=kz alakú helyettesítést természetesen 10γ és 1/10η helyett más k-val is alkalmazhatunk, pl. a k=2, 1/2, 5, 1/5 értékekkel a fellépő mellékszámítások könnyűek.
 

Székely Jenő (Pécs, Nagy Lajos g. III. o. t.)
 

Megjegyzés. Nomogramunkat fordítva az x1x2=q szorzat és az x1+x2=-p összeg leolvasására is lehet használni.