|
| Feladat: |
1030. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bácsy Zs. , Biborka T. , Bollobás B. , Bónis Katalin , Bornes Klára , Csizy L. , Durst I. , Farkas Z. , Fejes L. , Frint G. , Fritz József , Gálfi l. , Gazsi L. , Gombos Judit , Grüner Gy. , Györgyi János , Homitzky L. , Jahn A. , Katona Mária , Knuth E. , Kopornoky Zs. , Kovács Margit , Lendvai Katalin , Marót Ildikó , Marton D. , Marton Katalin , Meleghegyi L. , Miklóssy E. , Molnár E. , Nagy Dezső , Nagypál B. , Nováky B. , Pollai Marion , Porpáczy Erzsébet , Pribek F. , Sólyom I. , Szabó Péter , Szalay G. , Szarka Gy. , Szidarovszky Ágnes , Szilágyi G. , Szilvási I. , Szoboszlai L. , Torbágyi T. , Török Éva , Vaday G. , Várady Gábor |
| Füzet: |
1961/február,
60 - 63. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Síkgeometriai számítások trigonometriával, Körérintési szerkesztések, Feladat |
| Hivatkozás(ok): | Feladatok: 1960/február: 1030. matematika feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Egyszerűsítésül a szíj szélességét és vastagságát nem vesszük figyelembe, vagyis a tárcsák és a szíj által alkotott rendszernek a tengelyekre merőleges síkon levő vetületét tekintjük. A tárcsák vetülete , átmérőjű ill. kör, a középpontok , . A szíj vetülete pedig részből áll: és közös érintőinek az érintési pontok közötti és szakaszaiból, továbbá a körök egymástól elfordított és ívéből. Aszerint, hogy a szíj egyenes szakaszai keresztezik egymást vagy nem, az és szakaszok a belső, ill. külső közös érintőkön vannak. 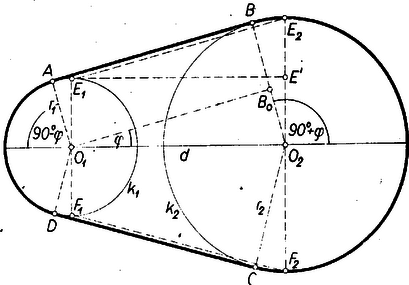 1. ábra
I. eset: nincs keresztezés. Legyen vetülete -n és (fokban mérve). Ekkor és a keresett távolság, valamint az érintőszakaszok hossza az derékszögű háromszögből (1. ábra) | | (1) |
A szíjjal fedett DA és BC ívekhez tartozó középponti szög 180-2φ, ill. 180+2φ. Így a szíj ismert h hosszából φ-re a következő egyenletet kapjuk: | DA^+BC^+2AB¯=2r1π180∘-2φ360∘+2r2π180∘+2φ360∘+2(r2-r1)ctg φ=h, | (2) |
ahonnan | ctgφ=h-(r1+r2)π2(r2-r1)-π180∘φ, |
és a számadatok alapján | ctg φ=8,834-0,01745 φ. | (3) |
(Előre gondolva arra, hogy négyjegyű táblázatot fogunk használni, π≈3,142-t vettünk, és a hányadosokból 4 értékes jegyet írtunk ki.) Vegyük észre, hogy (3) jobb oldalának 2-ik tagja éppen a φ szög ívmértéke, tehát ez a tag számítás nélkül ugyancsak közvetlenül kivehető a függvénytáblázatból.
(3)-at csak közelítőleg oldhatjuk meg, mert φ együtt lép fel egy trigonometrikus függvényével. Tekintettel arra, hogy φ együtthatója az állandó tagnak mintegy 500-ad része, első közelítésül vehetjük azt a φ1 szöget, amelyre
ctg φ1 = 8,834, azaz φ1 ≈6,46∘.
A jobb oldal így elhanyagolt tagja negatív, tehát ctg φ kisebb ctg φ1-nél, és ezért φ nagyobb φ1-nél. A 2-ik tag értéke φ1 mellett -0,113. A kotangens függvény ekkora változása φ1 környezetében kb. 0,1∘-kal növeli a szöget, ezért 2-ik és 3-ik közelítő értéknek φ2=6,5∘, ill. φ3=6,6∘-ot véve (3) bal és jobb oldalának értéke | φ2-vel: 8,777 és 8,721, ill. φ3-mal: 8,643 és 8,719, |
vagyis a bal oldal 0,056 többletet, ill. 0,076 hiányt mutat. Ezek szerint (3) gyöke φ2 és φ3 között van, valamivel közelebb φ2-höz. φ4=6,54∘ mellett (3) két oldalának eltérése már csak 8,723-8,720=0,003. Viszont φ5=6,55∘ és φ6=6,53∘ mellett a jobb oldal ismét 8,720, a bal oldal pedig 8,710, ill. 8,737 vagyis az eltérés nagyobb és ellentétes irányú.
További ‐ a fok ezredrészének meghatározását célzó finomítás táblázatunk alapján nem lehetséges, mert az ehhez szükséges lineáris interpoláció a kotangens-táblázat használt szakaszán a szokásosnál nagyobb hibával járna. Ugyanis 6∘ sorában a 0,1∘-onkénti csökkenések rendre: | 0,157,0,152,0,147,0,143,0,138,0,134,0,130,0,127,0,122,0,120, |
elég gyorsan változnak ‐ a sor elejétől a végéig mintegy 20%-kal ‐, ennélfogva a kotangens függvény grafikonja itt erősen görbül. A közbülső értékek pontosabb megállapítására viszont a lineáris interpolációnál pontosabb eljárást nem ismerünk. Eszerint (3) gyöke gyanánt a φ=φ4=6,54∘ értéket kell elfogadnunk.
Most már (1) alapján φ4-gyel d=527mm. És mivel φ5 és φ6-tal d-re 526, ill. 528 mm adódnék, vagyis csak 1 mm-rel eltérő érték, azért eredményünk megfelel a kívánt pontosságnak. 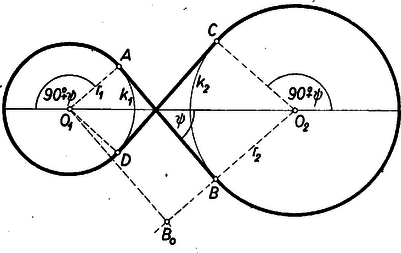 2. ábra
II. eset. Ha a szíj egyenes szakaszai keresztezik egymást, akkor a fenti O2B0 értéke r2+r1=140mm, továbbá (1) érvényes marad (2. ábra). A szíjjal fedett DA és BC ívek mindegyikéhez, φ helyett ψ jelöléssel, 180∘+2ψ, középponti szög tartozik, (2) helyére a | 2(r1+r2)(π180∘+2ψ360∘+ctg ψ)=h | (2') |
egyenlet, (3) helyére pedig a | ctg ψ=3,786-0,01745ψ | (3') |
egyenlet lép. Innen a fentiekhez hasonlóan és a keresett ψ érték ismét nagyobb ψ1-nél.
(3') elhanyagolt tagja ψ1 mellett -0,258. A kotangens függvény ekkora változása ψ1, környezetében kb. 1∘ növekedésre áll be, legyen ezért ψ2=15,8∘. Ekkor (3') két oldala 3,534, ill. 3,510. A bal oldal 0,024-nyi többletét a szög újabb 0,1∘-kal való növelésével majdnem eltüntethetjük:
ψ3=15,9∘mellett 3,511 - 3,508 = 0,003 többlet,
ψ4 = 16,0∘ mellett pedig 3,507-3,487=0,020 hiány
mutatkozik. Ezekből 0,01∘-nyi finomítással ψ≈15,91∘ adódik, evvel pedig a szíjtárcsák tengelyeinek távolsága (1) alapján d=510mm.
| Fritz József (Mosonmagyaróvár, Kossuth L. Gimn. III. o. t.) |
Megjegyzés. Több versenyző (3) és (3')-t ‐ vagy helyette a φ, ill. ψ-nek α, β pótszögére vonatkozó egyenletet ‐ a következő ugyancsak helyes alakokban írta:
-φ+ctg φ= 8,834, -ψ+ctg ψ=3,786,
-α+ctg α=7,264, -β+ctg β=2,216,
ahol a szögek ívmértékben értendők. Fent amiatt maradtunk meg a fok egységben való számolás mellett, mert a trigonometriai táblázat kezelése így egyszerűbb.
Mivel a szíj körív és egyenes részekre oszlik, eleve látható, hogy a kérdésre csak valamiféle próbálgató eljárás alapján válaszolhatunk. Erre utal a feladat kitűzésében a pontosság megszabása is. ‐ A próbálgatást a következő megoldás a szíjrészek keresztezés nélküli illesztése esetére egyenlet felállítása nélkül végzi.
II. megoldás: Tekintsük köreinknek az O1O2 centrálisra merőleges E1F1, E2F2 átmérőit ( O1E1 és O2E2 egyirányú sugarak), és legyen E1 vetülete O2E2-re E' (1. ábra). A szíj hosszát a körök egymástól elfordult E1F1 és F2E2 félkörívei és az F1F2, E2E1 szakaszok összegével helyettesítve hibát követünk el. Ez azonban nem lehet nagy, mert így az ívrészek összegét a kelleténél kisebbre, az egyenes részeket pedig nagyobbra vettük. Valóban, r2>r1 és az E1O1A, E2O2B szögek egyenlősége folytán a görbe rész feléből mellőzött E2B ív nagyobb a beiktatott E1A ívnél, viszont az E1E2 szakasz nagyobb AB-nél, mert E1E2 merőleges vetülete egy egyenesre (tehát nem nagyobb nála) az O1O2 szakasz, viszont AB az O1O2 merőleges vetülete, és így az előbbi a kisebb.
Ezek szerint a szíj félhosszából a két negyedkörív összegét levonva közelítő értéket kapunk E1E2-re, ebből pedig E'E2=60mm figyelembevételével az E1E2E' derékszögű háromszög alapján E1E'=O1O2-re. π≈3,142-del E1E2 ≈530,1 mm és O1O2≈526,7mm. Igyekezzünk most már úgy választ adni a kérdésre, hogy addig változtatjuk a két középpont távolságát, amíg az ebből kiszámítható szíjhosszúság egyenlő lesz az adott hosszúsággal.
O1O2-t 526,5mm-nek véve ‐ amely hossz éppen a határán van az 526 és 527mm-re kerekítendő értékeknek ‐ és mindenütt 4 értékes jegyre számítva egyrészt Pythagorász tétele alapján AB=523,1mm. Másrészt ‐ a körök külső hasonlósági pontját S-sel jelölve (ezt az 1. ábrán mellőztük) ‐ SO2:O1O2=r2:(r2-r1) alapján SO2=877,5, és így az SO5B derékszögű háromszögből az E2O2B-vel egyenlő O2SB szög 6,54∘, tehát a kisebb DA és a nagyobb BC ív középponti szöge 166,9∘, ill. 193,1∘, hosszuk 116,5 ill. 337,0mm. Ezek szerint így 116,5+337,0+2⋅523,1=1499,7mm hosszú szíjra lenne szükség, ennélfogva O1O2-t igen kis mértékben nagyobbra kell vennünk.
Nyilvánvaló, hogy ha O1O2-t 1mm-rel nagyobbra, 527,5mm-nek vennénk ‐ amely érték mm pontossággal már 528mm-t is adhat ‐, akkor a szíj hossza kb. 2mm-rel adódnék hosszabbnak; vagyis 1501,7mm körüli értéknek. Mivel pedig ez több a kívántnál, azért a középpontok távolsága mm pontossággal 527mm. (A becslést hasonló számítás igazolja.)
| Györgyi János (Budapest, Kölcsey F. Gimn. IV. o. t.) |
| Marton Katalin (Budapest, Fazekas M. Gyak. Gimn. IV. o. t.) |
|
|
 PDF |
PDF |  MathML
MathML 
