Kezdőlap


Feladat:	1029. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Albert I. , Bencsik I. , Bollobás Béla , Csikor F. , Fábián G. , Fajszi Cs. , Farkas Z. , Fekete J. , Frint G. , Fritz J. , Fukker G. , Gál J. , Grüner György , Hajna J. , Hanyi Zs. , Horváth Gaudi I. , Jahn A. , Knuth Előd , Kóta Gábor , Marton Katalin , Miklóssy E. , Molnár E. , Nagy Dezső , Nagypál B. , Pinkert A. , Rádai Á. , Rátkai J. , Sebestyén Z. , Sólyom I. , Szalay G. , Székács Gy. , Szilágyi G. , Szilvásy I. , Szoboszlai L. , Tóth Sándor , Vaday G. , Várady G.
Füzet:	1961/február, 57 - 60. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1960/február: 1029. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a két tükörkép $O_{1}$ , $O_{2}$ és válasszuk $k$ sugarát hosszúságegységnek. Ekkor a $k$ -ba írt szabályos háromszög oldala $\sqrt[]{3}$ , azt kell tehát bizonyítanunk, hogy $O_{1} O_{2} = d = \sqrt[]{3}$ . Jelöljük továbbá a szabályos $26$ -szög egy oldalának $O$ -ból való $360^{\circ} / 26 = 180^{\circ} / 13$ látószögét röviden 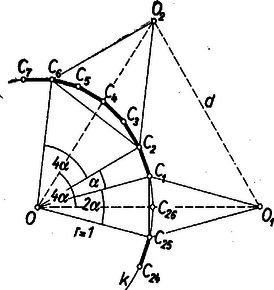$α$ -val.

O C_{25} O_{1} C_{1}

és

O C_{2} O_{2} C_{6}

négyszögek nyilvánvalóan egységnyi oldalú rombuszok, ezért

O_{1}

O C_{26}

O_{2}

pedig az

O C_{4}

félegyenesen van, tehát az

O_{1} O O_{2}

szög egyenlő

C_{26} O C_{4} ∢ = 4 α

-val. A rombuszok

O

-nál levő szöge

2 α

, ill.

4 α

, ezért

O O_{1} = 2 cos α

O O_{2} = 2 cos 2 α

. Most már az

O O_{1} O_{2}

háromszögből a koszinusz tétellel

\begin{matrix} O_{1} O_{2}^{2} = O O_{1}^{2} + O O_{2}^{2} - 2 O O_{1} \cdot O O_{2} cos 4 α, \\ d^{2} = 4 {cos}^{2} α + 4 {cos}^{2} 2 α - 8 cos α cos 2 α cos 4 α . \end{matrix}

Ezt az ismert

2 {cos}^{2} x = 1 + cos 2 x

azonosság felhasználásával írhatjuk így (a jobb oldalon a bizonyítandó

d^{2} = 3

állításra tekintettel különválasztjuk a

3

összeadandót):

\begin{matrix} d^{2} & = 2 (1 + cos 2 α + 1 + cos 4 α) - 8 cos α cos 2 α cos 4 α = \\ = 3 + 2 (\frac{1}{2} + cos 2 α + cos 4 α) - 8 cos α cos 2 α cos 4 α . & (1) \end{matrix}

Itt a jobb oldal harmadik tagja a 914. feladatban¹ bebizonyított

\begin{matrix} cos α cos 2 α cos 4 α ... cos 2^{n} α = \frac{sin 2^{n + 1} α}{2^{n + 1} sin α} \end{matrix}

azonosság szerint (

n = 2

-t írva) egyenlő

\begin{matrix} - 8 \frac{sin 2^{3} α}{2^{3} sin α} = - \frac{sin 8 α}{sin α} -val . \end{matrix}

(2)

A zárójelbeli kifejezés értékét pedig az

\begin{matrix} \frac{1}{2} + cos x + cos 2 x + cos 3 x + ... + cos n x = \frac{sin \frac{2 n + 1}{2} x}{2 sin \frac{x}{2}} \end{matrix}

azonosság alapján,²

x = 2 α

-val és

n = 2

-vel a

\begin{matrix} \frac{sin 5 α}{2 sin α} \end{matrix}

(3)

hányados adja meg. Ha még figyelembe vesszük, hogy

13 α = 8 α + 5 α = 180^{\circ}

, és így

sin 8 α = sin 5 α

, akkor valóban

\begin{matrix} d^{2} = 3 + \frac{sin 5 α}{sin α} - \frac{sin 8 α}{sin α} = 3, \end{matrix}

és ezt kellett bizonyítanunk.

Grüner György (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

Megjegyzések. I. Mindkét idézett azonosság legegyszerűbben a teljes indukció módszerével bizonyítható. Itt viszont mindkettőt

n = 2

-vel alkalmaztuk, oly kicsi számmal, amelyre a bizonyítás közvetlenül is elvégezhető az ismert

\begin{matrix} 2 cos x sin y = sin (x + y) - sin (x - y) és \\ 2 cos x cos y = cos (x + y) + cos (x - y) \end{matrix}

azonosságok alapján. Ugyanis

y = α

-val és előbb

x = 2 α

, majd

x = 4 α

-val

\begin{matrix} 2 cos 2 α sin α = sin 3 α - sin α, & (4) \\ 2 cos 4 α sin α = sin 5 α - sin 3 α, & (5) \end{matrix}

ezeket összeadva és hozzáadva még

sin α

-t mindkét oldalhoz (1) második tagja céljára

\begin{matrix} sin α (1 + cos 2 α + cos 4 α) = sin 5 α, \end{matrix}

ez pedig lényegében a (3) eredmény. Másrészt (1) harmadik tagja lépésről lépésre való alakítással

\begin{matrix} - 4 cos α (2 cos 2 α cos 4 α) = - 4 cos α (cos 6 α + cos 2 α) = \\ = - 2 (2 cos 6 α cos α + 2 cos 2 α cos α) = - 2 (cos 7 α + cos 5 α + cos 3 α + cos α), \end{matrix}

innen pedig a (4) és (5) mintájára képezett négy azonosság összeadásával (2)-re jutunk.

Kóta Gábor (Tatabánya, Árpád g. III. o. t.)

2. A fentieket továbbvíve a

cos 2 α = cos (13 α - 11 α) = cos (180^{\circ} - 11 α) = - cos 11 α

és

cos 4 α = - cos 9 α

egyenlőségek alapján (1) így is alakítható:

\begin{matrix} d^{2} = 3 + 1 - 2 (cos α + cos 3 α + cos 5 α + cos 7 α + cos 9 α + cos 11 α), \end{matrix}

elegendő tehát azt belátnunk, hogy a zárójelbeli kifejezés értéke

1 / 2

. Tekintsük evégett egy egységnyi oldalú szabályos

13

-szög hét egymás utáni oldalát ‐ az ábrán az

A B C D E F G H

nyitott poligont ‐ és vetítsük merőlegesen a csúcsokat az

A

-n át

H G

-vel párhuzamosan haladó

e

egyenesre.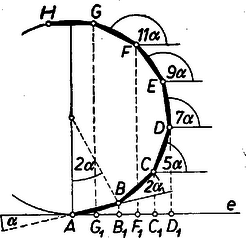

13

-szög mindegyik külső szöge

2 α

, az

A B

oldal

e

-vel bezárt szöge

α

, így az egymás utáni

A B, B C, C D, ..., F G

oldalak

e

-vel bezárt szöge rendre

α

3 α

5 α

7 α

9 α

11 α

(az utolsó három szög tompaszög). Ezért a zárójelbeli kifejezés tagjai az

A B, ..., F G

oldalak irányított vetületét:

{\vec{A B}}_{1}, ..., \vec{F_{1} G_{1}}

-et jelentik, pozitívnak véve az

A

-ból

B_{1}

-be,

B

vetületébe mutató irányt. Ennélfogva összegük

\begin{matrix} \vec{A B_{1}} + \vec{B_{1} C_{1}} + \vec{C_{1} D_{1}} + \vec{D_{1} E_{1}} + \vec{E_{1} F_{1}} + \vec{F_{1} G_{1}} = \vec{A G_{1}}, \end{matrix}

ez pedig valóban egyenlő

1 / 2

-del, mert a

13

-szög szimmetriája folytán az

A

-ban

e

-re emelt merőleges

K

-ban felezi

G H

-t, tehát

A G_{1} = K G

Marton Katalin (Budapest, Fazekas M. gyak. g. IV. o. t.)

3. A feladat állítása a komplex számsíkon végzett számítással is bizonyítható, abból kiindulva, hogy a szabályos

26

-szög csúcsainak a

26

-ik egységgyökök képeit vesszük.³

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

Knuth Előd (Budapest, I. István g. III. o. t.)

4. Többen a szögfüggvény-táblázatok felhasználásával azt mutatták meg, hogy az állítás

3

, vagy

4

értékes számjegynyi pontossággal igaz. E dolgozatokat hiányosnak minősítettük.

¹Lásd a megoldást K. M. L. XVIII. köt. 86. o. (1958. március), továbbá Faragó László: Mat. Szakköri Feladatgyűjtemény, 525. feladat (Középiskolai Szakköri Füzetek), Tankönyvkiadó, 1955. 52. o.

²Lásd az 1. jegyzetben idézett gyűjteményben, 527. feladat, 52. o.

³A felhasznált módszereket lásd pl. a következő műben: Reiman István: Geometriai feladatok megoldása a komplex számsíkon, Középiskolai Szakköri Füzetek. Tankönyvkiadó, 1957.