Kezdőlap


Feladat:	1023. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Biborka T. , Bollobás B. , Csikor F. , Farkas Z. , Fekete J. , Frint G. , Fritz J. , Gáti P. , Gazsi Lajos , Grüner Gy. , Györgyi János , Holop A. , Homitzky L. , Horváth S. , Kardeván P. , Kiss A. , Klimó J. , Knuth E. , Kóta G. , Krámli A. , Molnár E. , Nováky A. , Nováky B. , Páska Cs. , Pinkert A. , Pósch Margit , Szegő K. , Tihanyi A. , Várady G.
Füzet:	1960/december, 215 - 216. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Köréírt alakzatok, Négyzetek, Síkgeometriai számítások trigonometria nélkül sokszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1960/január: 1023. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C D E F = H$ hatszög csúcsai a feltételben szereplő szakaszpárok végpontjai között kétféle szerepet játszanak: $A$ , $C$ és $E$ 3-szor lép fel, $B$ , $D$ , és $F$ viszont $1$ -szer. A $3$ -ik szakaszpár úgy áll elő az elsőből, és a $2$ -ik a $3$ -ikból, hogy minden végpont helyére a $H$ körüljárása mentén rákövetkező második pontot írjuk; ezért egyrészt $A$ $C$ , $E$ , másrészt $D$ , $E$ , $F$ egymás között egyenrangúak. Ez az észrevétel bizonyításunkban rövidítéseket tesz lehetővé.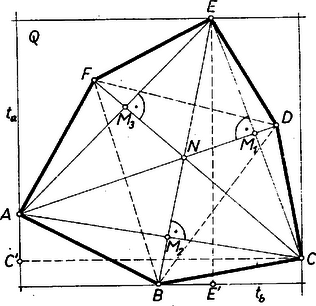

Megmutatjuk, hogy

H

-nak

A

C

E

-ben levő szöge derékszög. Ezt elég pl.

A

-ra bebizonyítani. Az

E A B = T_{1}

és

C F A = T_{2}

háromszögek egybevágók (azok a csúcsok felelnek meg egymásnak, amelyeknek a felsorolásbeli sorszáma egyenlő). Ugyanis az

E

-ben, ill.

C

-ben összefutó oldalaik a feltevés szerint páronként egyenlők, és a köztük levő szög is mindkettőben ugyanakkora, mert merőleges szárú hegyes szögek. Valóban, mindkét szög kisebb derékszögnél, mert az

E A

és

C F

, az

E B

és

C A

, a

B E

és

C F

átlópárok

M_{3}

, ill.

M_{2}

, ill.

N

metszéspontja

H

konvexsége folytán benne van

H

-ban, ezért az

A E B

szög azonos az

M_{3} E N

szöggel, és az

F C A

szög az

N C M_{2}

szöggel, az utóbbi szögek pedig az

M_{3} E N

N C M_{2}

derékszögű háromszögnek a derékszögtől különböző szögei. Ebből következik, hogy

T_{1}

és

T_{2}

körüljárása megegyező, egymással a síkjukban végzett mozgatással hozhatók fedésbe. És mivel a feltételben szereplő oldalpárjaik egymásba

90^{\circ}

-os forgatással átvihetők, azért ugyanez áll harmadik oldalaikra,

A B

és

F A

-ra is. Másképpen: az

F A B

háromszög

A

-nál derékszögű és egyenlő szárú. (Könnyű belátni, hogy a forgatás középpontja a

B F

szakasz felezőpontja.)
Ugyanígy a

B C D

és

D E F

is egyenlő szárú derékszögű háromszögek. Ezért a

B

D

F

-nél levő szögek mindegyike tompaszög, mert

2 \cdot 45^{\circ} = 90^{\circ}

-kal nagyobb a

B D F

háromszög megfelelő szögénél, másrészt

H

konvexsége folytán (valóságos hatszögben) kisebb

180^{\circ}

-nál. Az

A B C

szög

A B E \equiv A B M_{2}

és

E B C \equiv M_{2} B C

rész szögei azonban hegyes szögek, mert az

A B M_{2}

, és

M_{2} B C

derékszögű háromszögekben a derékszög

M_{2}

-nél van. Ugyanez áll a

D

és

F

-nél levő szögek

D A

, ill.

F C

két oldalán levő részeire.
Az

A

C

E

csúcsok

H

minden

Q

támasz téglalapjának kerületi pontjai, mert ha pl. a

B A F

derékszög csúcsán át párhuzamosokat húzunk

Q

oldalaival, akkor vagy egyikük kettévágja a

B A F

szögtartományt, és így a rá merőleges egyenes támaszegyenese

H

-nak, vagy egybeesnek

A B

és

A F

-fel, és így

A

Q

-nak csúcsa. Ekkor

B

és

F

Q

kerületén van. ‐ Másrészt a

B

D

F

csúcsok közül legalább egy

Q

kerületén van, mert ha

A

C

E

mindegyikében a támasz egyenes különböző

H

oldalaitól, ezek

Q

-nak csak három oldalát adják meg. ‐ Viszont

B

D

F

közül legfeljebb kettő lehet a kerületen és nyilvánvaló, hogy ilyenkor a

H

-nak köztük levő csúcsa egyben

Q

-nak is csúcsa. ‐

B

D

F

mindegyike csak akkor lehetne

Q

kerületén, ha egyikükben

H

-nak

180^{\circ}

-os szöge volna.
Az eddigiek szerint elég

H

azon támasz téglalapjairól megmutatnunk, hogy származtató támasz sávjaik szélessége egyenlő, amelyek kerületén legalább a

C

E

A

és

B

csúcsok rajta vannak.

H

körüljárásából nyilvánvaló, hogy e téglalapokban

B

és

E

, valamint

A

és

C

egy-egy szemben fekvő oldalpáron vannak. Ha már most

Q

két oldala merőleges

B E

-re, akkor a másik kettő merőleges

A C

-re, így a

Q

-t meghatározó két támaszsáv szélessége

B E

, ill.

A C

, és ezek egyenlősége folytán

Q

négyzet. Ha pedig

E

-nek,

C

-nek a

B

-beli

t_{b}

, ill. az

A

-beli

t_{a}

támaszegyenesen levő

E'

, ill.

C'

vetülete

B

-től,

A

-tól különböző, akkor a sávok szélessége

E E'

, ill.

C C'

, és ezek egyenlők, mert a

B E E'

és

A C C'

egybevágó derékszögű háromszögeknek megfelelő befogói (ezekben az átfogók és az

E

-nél,

C

-nél levő merőleges szárú hegyesszögek egyenlők).
Ezzel az állítást bebizonyítottuk.

Györgyi János (Budapest, Kölcsey F. g. IV. o. t.)

Megjegyzés. Az

F A B

B C D

és

D E F

háromszögek derékszögű egyenlő szárú volta a 957. feladat II. megoldásához fűzött megjegyzés tételéből is következik, ugyanis a feltevések folytán

B

D

F

E A C

háromszögből úgy származtathatók, hogy a magasság vonalakra a csúcsoktól a szemben fekvő oldal felé felmérjük a szemben levő oldal hosszát.

Gazsi Lajos (Kaposvár, Táncsics M. g. IV. o. t.)