Kezdőlap


Feladat:	1022. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bíborka T. , Bollobás B. , Csikor F. , Farkas Z. , Fekete J. , Frint G. , Fritz J. , Gagyi Pálffy András , Gazsi L. , Grüner Gy , Holop A. , Horváth S. , Kiss Á. , Klimó J. , Knuth Előd , Máté A. , Máté Zs. , Székely J. , Tihanyi A. , Várady G.
Füzet:	1961/január, 8 - 11. oldal		PDF \| MathML
Témakör(ök):	Szabályos testek, Poliéderek szimmetriái, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1960/január: 1022. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szóban forgó $P$ poliéder háztető alakjára tekintettel nevezzük az $E F = b$ élt röviden $P$ gerincének (1. ábra).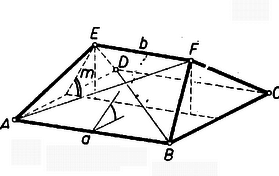

1. ábra

a

és

b

élek között ‐ az idézett versenyfeladat megoldása szerint ‐ az

a b + b^{2} = a^{2}

összefüggés áll fenn, eszerint

b = a (\sqrt[]{5} - 1) / 2 \approx 0, 618 a

; a gerincnek a négyzetlaptól való

m

távolságára pedig

m^{2} = a (a - b) / 4

, vagyis az előbbi összefüggés alapján

m = b / 2 \approx 0, 309 a

. ‐ Nyilvánvaló, hogy

P

-nek két szimmetriasíkja van: a

B C

és az

A B

él felező merőleges síkja, az előbbi magában foglalja a gerincet.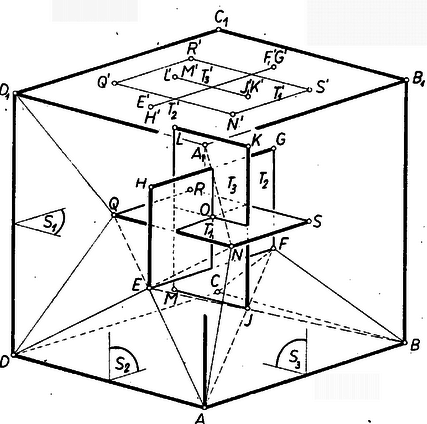

2. ábra

Legyen a kocka alap- és fedőlapja

A B C D

és

A_{1} B_{1} C_{1} D_{1}

és legyenek

A A_{1}

...

D D_{1}

, a párhuzamos oldalélek. Legyen az alap- és a fedőlapra állított

P_{a}

P_{f}

poliéder pár

E F

, ill.

G H

gerince párhuzamos a kocka

A B

élével (2. ábra), az

A B B_{1} A_{1}

elő- és a

D C C_{1} D_{1}

hátlapra illesztett poliéderek

J K

, ill.

L M

gerince párhuzamos

A A_{1}

-gyel, végül az

A D D_{1} A_{1}

bal és a

B C C_{1} B_{1}

jobb oldallapra illesztett poliéderek

N Q

, ill.

R S

gerince párhuzamos

A D

-vel. Ekkor bármelyik szomszédos kockalap párra illesztett poliéder-pár gerincei merőlegesek egymásra, megfelelnek a követelménynek. Továbbá a párhuzamos gerincpárok benne vannak a kocka azon

S_{2}

S_{3}

, ill.

S_{1}

szimmetriasíkjában, amelyek merőlegesen felezik az

A D

-vel,

A B

-vel, ill.

A A_{1}

-gyel párhuzamos éleket.
Így a leírandó

I

test

12

csúcsa

3

jól áttekinthető csoportba osztható: a párhuzamos gerincpárok

4 - 4

végpontja egy-egy téglalapot határoz meg. Valóban, pl. az

S_{2}

-ben fekvő

E F G H = T_{2}

négyszög paralelogramma, mert

E F # G H

, továbbá szögei derékszögek, mert

P_{a}

és

P_{f}

beállításuknál fogva egymás tükörképei

S_{1}

-re, ezért

E H

és

F G

párhuzamosak

A A_{1}

-gyel, merőlegesek

A B

-re, és így

E F

-re is. Hasonlóan adódik, hogy a

J K L M = T_{3}

és az

N Q R S = T_{1}

négyszögek ugyancsak téglalapok. Ezek szerint az

I

poliéder a kocka

S_{1}

S_{2}

S_{3}

szimmetriasíkjai mindegyikére tükrös. ‐ Másrészt a három téglalap egybevágó, mert két-két oldaluk gerinc, a másik kettő pedig két párhuzamos gerinc távolsága:

a - 2 m = a - b

. Az utóbbi a kisebb oldal, mert az idézett eredmény szerint

b > a / 2

.
Nyilvánvaló továbbá, hogy mindhárom téglalap középpontja azonos a kocka

O

középpontjával; tehát ettől mind a

12

csúcs egyenlő távolságra van,

I

köré

O

középponttal gömb írható.
Tekintsük

I

csúcsainak a kocka

D

-ben összefutó lapjaira való vetületét. Ezeket ‐ az oldallapot

D D_{1}

körül a hátlap síkjába, majd a hátlappal együtt

D C

körül az alaplap síkjába forgatva mutatja a 3. ábra, a vetületeket ugyanúgy jelöltük, mint magukat a pontokat (a fedőlapon levő vetületeket a 2. ábra mutatja.)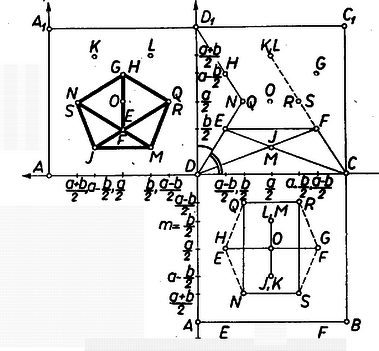

3. ábra

Az alapsíkon

T_{1}

vetülete valódi nagyságban látszik,

T_{2}

és

T_{3}

vetülete pedig egyenes szakasz,

2 - 2

csúcsuk vetülete egybeesik, pl.

E

H

, ill.

J

K

, így a

12

csúcs vetülete

8

pont.

T_{1}

vetülete magában foglalja

T_{3}

vetületét, ugyanis az utóbbi a

T_{1}

-nek

b

hosszúságú tengelyébe eső,

O

vetületére szimmetrikus,

a - b

hosszúságú szakasz.

T_{2}

vetülete viszont kinyúlik

T_{1}

vetületéből, mert hossza

b

és ez a

T_{1}

-nek

a - b

hosszúságú tengelyére esik. Hasonló megállapításokat tehetünk

I

csúcsainak a kocka hátlapján és oldallapján levő vetületeiről.
Így az

I

poliéder mindhárom vetületének körvonala (kontúrja) két szimmetria-tengellyel bíró hatszög, melynek két szemben fekvő csúcsa két-két testcsúcs egybeeső vetülete.

I

konvexségéből és az alapsíkon levő vetületből következik, hogy az alapsíkra merőleges

E H N

síkban

I

-nek határlapja van, mert az

E

H

N

pontok vetületei beletartoznak a vetület körvonalába és

I

minden csúcsának vetülete az

E

H

N

pontok vetületével meghatározott egyenes egyik oldalán fekszik. Ez a határlap az

E H N

háromszög, mert

I

egy további csúcsának vetülete sem esik az

E H N

vetületére. Hasonlóan látható be a három vetületből, hogy az

\begin{matrix} E H Q, F G R, F G S; J M E, J M F, K L G, K L H; N S J, N S K, Q R L, Q R M \end{matrix}

háromszögek

I

-nek lapjai.
Ezek azt is jelentik, hogy e háromszögek oldalai

I

-nek élei. Így pl. az

E

csúcsot legalább a

H

N

Q

J

M

csúcsokkal kötik össze élek. Megmutatjuk, hogy ennek az

5

élnek a közös hossza

E H = a - b

.
A

P

poliédernek az idézett versenyfeladat szerint meghatározó tulajdonsága, hogy egyenlő szárú trapéz és egyenlő szárú háromszög lapjának a négyzetlappal alkotott szögei pótszögek (1. ábra egy- és két íves szöge). Ezért két szomszédos kockalapra állított

P

-nek egy-egy lapsíkja egybeesik, pl. a

P_{a}

-beli

A B F E

trapézlap és a

P_{e}

-beli

A B J

háromszöglap. Másrészt a 951. feladatban bebizonyítottuk, hogy egy trapézlap és egy háromszöglap alkalmas összeillesztésben szabályos ötszöget ad. Ebből következik, hogy a háromszögnek az alapon fekvő szögei

36^{\circ}

-osak (4. ábra), ugyanekkora szögeket zárnak be a trapéz átlói a párhuzamos oldalakkal, és az átlók egymást

b

és

a - b

hosszúságú részekre osztják.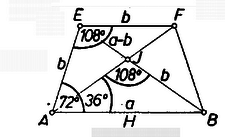

4. ábra

Ezek szerint

J

A B F E

trapéz

A F

és

B E

átlóinak metszéspontjában van és

E J = a - b

. Az

I

szimmetriája folytán ugyanekkora

E M

is. Ugyanezen meggondolást

P_{a}

és

P_{b}

-re alkalmazva

E N = E Q = a - b

.
Megmutatjuk, hogy

E

-ből nem indul ki más él. Az

E

-ből kiinduló, vizsgált öt él egyenlősége azt jelenti, hogy az élek

H

N

J

M

Q

végpontjai az

E

középpont körüli

a - b

sugarú gömbön vannak. Ez a gömb az

I

köré írt gömböt körben metszi, ami síkidom, tehát az öt végpont egy síkban van. ‐ A fentiekhez hasonlóan látható be, hogy a

H N

N J

J M

M Q

Q H

, szakaszok hossza ugyancsak

a - b

, ezért a

H N J M Q

síkidom körbe írható egyenlő oldalú ötszög (5. ábra), vagyis szabályos ötszög.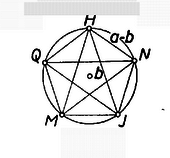

5. ábra

Ezért a

H J

N M

J Q

M H

és

Q N = b

átlók e szabályos ötszögnek, és így

I

-nek is a belsejében vannak,

I

-nek a konvexség folytán nem élei. Most már, mivel ugyanígy

H

N

J

M

Q

mindegyikéből

5 - 5

él indul ki, és ezek végpontjai

1 - 1

szabályos ötszöget határoznak meg, és ezekben az

E F

E R

E L

E K

E S

szakaszok átlók, azért nem élei

I

-nek. Végül

E G

sem éle

I

-nek, mert a körülírt gömbnek átmérője. Így

E

-ből valóban csak az említett

5

él indul ki.
Ezek az élek a

H N J M Q

ötszög

a - b

hosszúságú oldalaival szabályos háromszögeket alkotnak, tehát

I

-nek

E

-ben öt ilyen lapja fut össze.
Ugyanez áll

I

minden csúcsára, mert

I

előállításában mind a hat

P

egyenlő szerepet játszott, ezért

I

minden éle egyenlő, minden lapja szabályos háromszög. Ezek alapján az élek száma

12 \cdot 5 / 2 = 30

12 \cdot 5

szorzatban minden él mindkét végpontjánál figyelembe van véve, ezért osztunk

2

-vel). A lapok száma pedig hasonlóan

12 \cdot 5 / 3 = 20

.
Mindezek szerint az

I

poliéder ún. szabályos ikozaéder (húszlapú test).

Knuth Előd (Budapest, I. István Gimn. III. o. t.)

Megjegyzés. Számítással is meg lehet mutatni, hogy az

I

-t meghatározó

12

csúcsból képezett bármely pár egymástól való távolságai között csak

3

-féle hosszúság lép fel:

a - b

b

és a

T

téglalapok átlói (az utóbbiak nyilván nem lehetnek élek). Ugyanis a

P

méreteire idézett eredmények alapján

a

és

b

-vel kifejezhetjük bármely csúcsnak pl. a kocka

D

-ben összefutó lapjaitól való távolságát. Ezek a 2. ábra

D

-ből

C

A

D_{1}

felé mutató ,,tengelyein'' láthatók. Ezek alapján pl. az

E K

távolságot azon téglatest testátlójaként számíthatjuk ki, melynek két csúcsa

E

K

, és lapjai párhuzamosak a kocka lapjaival. E téglatest

D C

irányú szélessége,

D A

irányú kiterjedése és

D D_{1}

, irányú magassága, mint

E

és

K

megfelelő távolságainak különbsége (abszolút értékben véve) rendre a következő:

\begin{matrix} \frac{a}{2} - \frac{a - b}{2} = \frac{b}{2}, \frac{a}{2} - \frac{b}{2} = \frac{a - b}{2}, \frac{a + b}{2} - \frac{b}{2} = \frac{a}{2}, \end{matrix}

és így az

E K

testátló négyzete, a megoldás elején idézett összefüggések alapján

\begin{matrix} \frac{1}{4} [a^{2} + b^{2} + {(a - b)}^{2}] = \frac{1}{2} [(a^{2} - a b) + {b'}^{2}] = \frac{1}{2} (b^{2} + b^{2}) = b^{2}, \end{matrix}

és így

E K = b

. Hasonlóan

\begin{matrix} E J^{2} = {(\frac{a}{2} - \frac{a - b}{2})}^{2} + {(a - \frac{b}{2} - \frac{a}{2})}^{2} + {(\frac{b}{2} - \frac{a - b}{2})}^{2} = \\ = & \frac{1}{4} [b^{2} + (a^{2} - 2 a b + b^{2}) + (4 b^{2} - 4 a b + a^{2})] = \\ = & \frac{1}{2} [(a^{2} - 3 a b + 2 b^{2}) + b^{2}] = \frac{1}{2} [(a^{2} - 3 a b + 2 b^{2}) + (a^{2} - a b)] = \\ = & a^{2} - 2 a b + b^{2} = {(a - b)}^{2}, \end{matrix}

és így

E J = a - b

Gagyi Pálffy András (Budapest, Széchenyi I. g. III. o. t.)