Kezdőlap


Feladat:	1021. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Fejes László , Máté Zsolt , Várady Gábor
Füzet:	1960/december, 213 - 215. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Húrnégyszögek, Számtani sorozat, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1960/január: 1021. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A négytagú számtani sorozat két szélső és két közbülső tagjának összege egyenlő:

\begin{matrix} α + γ = β + δ, \end{matrix}

(1)

eszerint négyszögünk húrnégyszög. Legyenek másrészt az átlókkal kettévágott szögek részei rendre

D A C = α_{1}

C A B = α_{2}

A B D = β_{1}

D B C = β_{2}

B C A = γ_{1}

A C D = γ_{2}

C D B = δ_{1}

B D A = δ_{2}

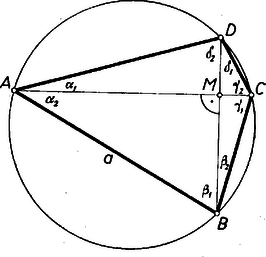Így, mivel háromtagú számtani sorozat összege egyenlő a középső tag háromszorosával, az

A B D

háromszögből

β_{1} = 60^{\circ}

. A négyszög körbe írható volta és az átlók merőlegessége folytán

γ_{2} = 60^{\circ}

δ_{1} = α_{2} = 30^{\circ}

, továbbá

β_{2} = α_{1}

. Ezért a négytagú sorozat különbsége

ε = β - α = (β_{1} + β_{2}) - (α_{1} + α_{2}) = 60^{\circ} - 30^{\circ} + (β_{2} - α_{1}) = 30^{\circ}

, tehát (1)-re és a négyszög szögeinek összegére tekintettel

α + γ = α + (α + 3) = 2 α + 90^{\circ} = 180^{\circ}

-ból

α = 45^{\circ}

β = 75^{\circ}

δ = 105^{\circ}

γ = 135^{\circ}

, továbbá

α_{1} = β_{2} = 15^{\circ}

γ_{1} = δ_{2} = 75^{\circ}

. Ezek szerint az

A B C

háromszög egyenlő szárú,

A C = A B = 1

.
Most már a szinusz-tétel ismételt alkalmazásával a további oldalak és átló

\begin{matrix} az & A B C & háromszögből & B C = sin 30^{\circ} : sin 75^{\circ} & \approx 0, 5176; \\ " & A B D & " & A D = sin 60^{\circ} : sin 75^{\circ} & \approx 0, 8966; \\ " & A B D & " & B D = sin 45^{\circ} : sin 75^{\circ} & \approx 0, 7321; \\ " & A C D & " & C D = sin 15^{\circ} : sin 105^{\circ} & \approx 0, 2679 egység, \end{matrix}

és végül az átlók merőlegessége folytán szorzatuk feléből a négyszög területe

t = B D / 2 = 0, 3660

területegység.

Máté Zsolt (Szeged, Radnóti M. g. IV. o. t.)

Megjegyzések. 1. Ha a szinusz függvény összeadási (addíciós) tétele alapján ismertnek tekintjük a

\begin{matrix} sin 75^{\circ} = sin (45^{\circ} + 30^{\circ}) = \frac{1}{\sqrt[]{2}} \cdot \frac{\sqrt[]{3}}{2} + \frac{1}{\sqrt[]{2}} \cdot \frac{1}{2} = \frac{\sqrt[]{3} + 1}{2 \sqrt[]{2}} és \\ sin 15^{\circ} = sin (45^{\circ} - 30^{\circ}) = \frac{\sqrt[]{3} - 1}{2 \sqrt[]{2}} \end{matrix}

értékeket, akkor eredményeinket a táblázat, vagyis tizedes alakú közelítő törtek használata nélkül, pontos, ,,zárt'' alakban is felírhatjuk:

\begin{matrix} B C = (\sqrt[]{6} - \sqrt[]{2}) / 2, A D = (3 \sqrt[]{2} - \sqrt[]{6}) / 2, B D = \sqrt[]{3} - 1, \\ C D = 2 - \sqrt[]{3} és t = (\sqrt[]{3} - 1) / 2. \end{matrix}

Fejes László (Makó, József A. g. IV. o. t.)

2. Ezekhez az eredményekhez trigonometriai ismeretek nélkül, csupán a Püthagorász-tétel ismételt alkalmazásával és némi ügyeskedéssel is eljuthatunk. Az átlók metszéspontját

M

-mel jelölve az

A B M

derékszögű háromszögből

B M = 1 / 2

A M = \sqrt[]{3} / 2

. Így

M C = A C - A M = (2 - \sqrt[]{3}) / 2

, és egyrészt a

B C M

derékszögű háromszögből

\begin{matrix} B C = \sqrt[]{\frac{1}{4} + \frac{7 - 4 \sqrt[]{3}}{4}} = \sqrt[]{\frac{6 - 2 \sqrt[]{6 \cdot 2} + 2}{4}} = \frac{\sqrt[]{6} - \sqrt[]{2}}{2}, \end{matrix}

másrészt

C D M

-ből

C D = 2 M C = 2 - \sqrt[]{3}

és

M D = M C \sqrt[]{3} = (2 \sqrt[]{3} - 3) / 2

, ennélfogva

B D = B M + M D = \sqrt[]{3} - 1

. Végül

D A M

-ből

\begin{matrix} D A = \sqrt[]{\frac{3}{4} + \frac{21 - 12 \sqrt[]{3}}{4}} = \sqrt[]{\frac{18 - 2 \sqrt[]{18 \cdot 6} + 6}{4}} = \frac{\sqrt[]{18} - \sqrt[]{6}}{2} . \end{matrix}

Várady Gábor (Győr, Révai M. g. IV. o. t.)

3. Az előző megjegyzésnek az

A B C

háromszögre vonatkozó gondolatát bármely hegyes

α

szögre alkalmazva az értékes, de kevésbé ismert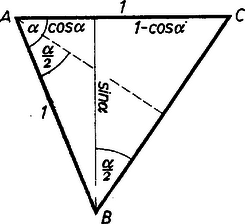

\begin{matrix} tg \frac{α}{2} = \frac{1 - cos α}{sin α} \end{matrix}

összefüggéshez jutunk; ugyanis

B M = sin α

A M = cos α

C M = 1 - cos α

, továbbá

C ∢ = (180^{\circ} - α) 2 = 90^{\circ} - α / 2

és így

C B M ∢ = α / 2

4. Néhány dolgozat az

A B D

háromszög

60^{\circ}

-os szögét

A

, vagy

D

-hez téve az

α = 60^{\circ}

β = 80^{\circ}

, ill.

α = 67, 5^{\circ}

β = 82, 5^{\circ}

esetet is kidolgozta

2

-ik, ill.

3

-ik megoldásként. A szövegben azonban nem az áll, hogy az

A B D

háromszög szögei valamilyen sorrendben alkotnak számtani sorozatot, hanem hogy ez az egymás utáni szögekre, vagyis az

A

B

D

csúcsú szögre áll.