Kezdőlap


Feladat:	1020. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bollobás B. , Csikor F. , Dömötör Gy. , Farkas Z. , Frint G. , Fritz J. , Gáti Pál , Hahn J. , Holop J. , Horváth S. , Kiss Á. , Klimó J. , Knuth E. , Kóta G. , Kóta J. , Máté A. , Máté E. , Máté Zs. , Páska Cs. , Simonovits M. , Székely J.
Füzet:	1960/november, 132 - 134. oldal		PDF \| MathML
Témakör(ök):	Abszolútértékes egyenlőtlenségek, Négyzetrács geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1960/január: 1020. matematika feladat

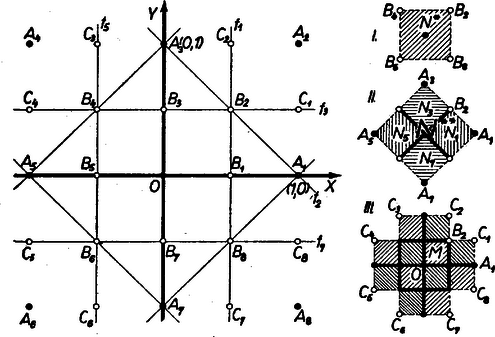
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $O$ origóhoz legközelebb vannak az $A_{1} (1, 0)$ , $A_{3} (0, 1)$ , $A_{5} (- 1, 0)$ és $A_{7} (0, - 1)$ rácspontok, távolságuk $O A_{2 k - 1} = 1 (k = 1, 2, 3, 4)$ , ezek $O$ legközelebbi szomszédai. Ezek után legkisebb az $O A$ a távolság az $A_{2} (1, 1)$ , $A_{4} (- 1, 1)$ , $A_{6} (- 1, - 1)$ , $A_{8} (1, - 1)$ pontokra: $O A_{2 k} = \sqrt[]{2}$ $(k = 1, 2, 3, 4)$ .
Egy az I. követelménynek eleget tevő pontot $P$ -vel és egy a $P$ körül írt $k$ kör sugarát $r$ -rel jelölve $O$ akkor és csak akkor van $k$ kerületén vagy a belsejében, ha $O P \leq r$ , és $A_{1}$ akkor külső pont $k$ -ra nézve, ha $r < A_{1} P$ . Ezért $O P < A_{1} P$ , vagyis $P$ -nek az $O A_{1}$ szakasz $f_{1}$ felező merőlegeséhez képest azon az oldalon kell lennie, amelyen $O$ van. Ezt a követelményt $P$ abszcisszájával $x < 1 / 2$ alakban írhatjuk fel, ugyanis $f_{1}$ egyenlete $x = 1 / 2$ .
Hasonlóan: ahhoz, hogy $k$ tartalmazhassa $O$ -t, de ne tartalmazza $A_{3}$ -at, $A_{5}$ -öt, illetve $A_{7}$ -et, kell, hogy $P$ az $O A_{3}$ , $O A_{5}$ , $O A_{7}$ szakasz $f_{3}$ , $f_{5}$ , $f_{7}$ , felező merőlegesének $O$ -t tartalmazó oldalán legyen. Ehhez szükséges és elegendő, hogy $P$ koordinátáira álljon:

\begin{matrix} y < 1 / 2, ill. x > - 1 / 2, ill. y > - 1 / 2. \end{matrix}

Avégett, hogy

k

tartalmazza

O

-t, de

A_{1}

A_{3}

A_{5}

A_{7}

egyikét se tartalmazza, mind a négy feltételnek teljesülnie kell,

P

-nek az

f_{1}

f_{5}

és

f_{3}

f_{7}

egyenespárokkal határolt síksávok közös belső pontjának, a

B_{2} B_{4} B_{6} B_{8} = N^{*}

négyzet belső pontjának kell lennie, amelynek csúcsai a

B_{2} (1 / 2, 1 / 2)

B_{4} (- 1 / 2, 1 / 2)

B_{6} (- 1 / 2, - 1 / 2)

B_{8} (1 / 2, - 1 / 2)

pontok. Mindez ahhoz is elegendő, hogy

k

ne tartalmazza

A_{2 k}

-t se, mert

N^{*}

belseje teljesen

O A_{2 k}

felező merőlegesének

O

-t tartalmazó oldalán van (lásd pl. az

O A_{2}

szakasz

A_{1} A_{3}

felező merőlegesét). Még-inkább áll ez az

O

-tól távolabbi rácspontokra, ennélfogva az I. követelménynek

N^{*}

belső pontjai és csak ezek tesznek eleget. A

P

koordinátáira talált négy követelményt a következő kettőbe vonhatjuk össze:

| x | < 1 / 2

és

| y | < 1 / 2

.
A II-ben előírt,

O

-n felüli egyetlen rácspont csak valamelyik

A_{2 k - 1}

lehet. Ha ugyanis volna olyan

P

közepű

k

, amely (az

O

-n felül) pl.

A_{2}

-t tartalmazza, de

A_{1}

-et és

A_{3}

-at nem, ebből az I. esethez hasonlóan adódnék, hogy

P

f_{3}

és

f_{1}

-nek

A_{2}

-t tartalmazó oldalán van. Ekkor viszont fennáll

P A_{3} < P O

és

P A_{1} < P O

, és ez ellentmond a feltevésnek.

Keressük tehát először azon

k

körök

P

középpontjának helyét, amelyek tartalmazzák

O

-t és

A_{1}

-et, de további rácspontot nem. Így

P O < P A_{2}

és

P O < P A_{8}

, ezért

P

O A_{2}

O A_{3}

szakasz

A_{1} A_{3}

, illetve

A_{1} A_{7}

felező merőlegesének

O

-t tartalmazó oldalán van, másrészt

P A_{1} < P A_{3}

és

P A_{1} < P A_{7}

, ezért

P

-nek az

O A_{2}

O A_{8}

egyenes

A_{1}

-et tartalmazó oldalán, vagyis az

O B_{8} A_{1} B_{2} = N_{1}

négyzet belsejében kell lennie. Az ilyen

P

körüli

k

‐ ha nem tartalmazza

A_{2}

A_{3}

A_{7}

A_{8}

egyikét sem, ‐ akkor nyilván más rácspontot sem, ezért

N_{1}

minden belső pontja megfelel II-nek.
Hasonlóan mindazok a

P

középpontok, amelyek körül van olyan

k

, melyben az

O

-n felüli egyetlen rácspont az

A_{3}

, az

A_{5}

, ill. az

A_{7}

, rendre az

O B_{2} A_{3} B_{4} = N_{3}

O B_{4} A_{5} B_{6} = N_{5}

O B_{6} A_{7} B_{8} = N_{7}

, négyzet belső pontjai, és csak ezek.
Mivel pedig II. csak úgy teljesül, ha

k

O

-t, továbbá vagy

A_{1}

-et, vagy

A_{3}

-at, vagy

A_{5}

-öt, vagy

A_{7}

-et tartalmazza, azért

P

-nek vagy

N_{1}

, vagy

N_{3}

, vagy

N_{5}

, vagy

N_{7}

belsejében kell lennie. Így is mondhatjuk:

P

csak az

A_{1} A_{3} A_{5} A_{7} = N^{* *}

négyzet belsejében lehet, de nem lehet rajta a

B_{2} B_{6}

B_{4} B_{8}

oldalfelezőkön. Ezt a feltételt

P

koordinátáival így lehet kifejezni:^{$^{*}$}

\begin{matrix} | x | + | y | < 1, de | x | \neq | y | . \end{matrix}

A III. követelményben

O

-n felül előírt két további rácspont nem lehet egymástól 2 egységnyi távolságra, mint pl.

A_{1}

és

A_{5}

. Ezt ugyanis így mondhatnók:

k

tartalmazza az

O

A_{1}

rácspontpárt, de

A_{2}

A_{8}

A_{3}

A_{7}

-et nem, ezért ‐ mint a II-ben láttuk ‐

P

N_{1}

-belsejében van, továbbá

k

tartalmazza az

O

A_{5}

párt, de nem tartalmazza

A_{4}

A_{6}

A_{3}

A_{7}

-et, ezért

P

N_{5}

belsejében van. Már pedig

N_{1}

és

N_{5}

belsejének nincs közös pontja. ‐ Nyilván még kevésbé lehet a két pont egymástól nagyobb távolságra, ezért

O

és a két további rácspont csak egy derékszögű egyenlő szárú háromszög csúcsai lehetnek.
Ha ez a 3 pont pl.

O

A_{1}

A_{3}

, akkor a

P A_{1} < P A_{2}

P A_{3} < P A_{7}

P A_{3} < P A_{2}

, és

P A_{1} < P A_{5}

követelmények folytán

P

csak az

O B_{1} B_{2} B_{3} = M

négyzet belsejében lehet. Végigmenve a további két pont minden lehetséges megválasztásán (

A_{1}

és

A_{2}

A_{1}

és

A_{3}

A_{1}

és

A_{7}

stb., 12 eset)

P

számára a

C_{1} B_{2} C_{2} C_{3} B_{4} C_{4} C_{5} B_{6} C_{6} C_{7}

B_{8} C_{8}

idom belsejét kapjuk, ahol

C_{k}

A_{k} A_{k - 1}

szakasz felező pontja (

1 \leq k \leq 8

A_{9}

-nek

A_{1}

tekintendő), kivéve azonban az idomból

N^{*}

kerületének és

A_{1} A_{5}

A_{3} A_{7}

tengelyeknek pontjait.

P

koordinátáival kifejezve a következő két feltételcsoportból legalább az egyiknek kell teljesülnie:

\begin{matrix} III. a) & | x | < 1, | y | < 1 / 2, x \neq 0, | x | \neq 1 / 2; \\ b) & | x | < 1 / 2, | y | < 1, y \neq 0, | y | \neq 1 / 2. \end{matrix}

Ezzel eleget tettünk a feladat utasításának.

Gáti Pál (Pécs, Nagy Lajos g. III. o. t.)

^{$^{*}$}Bővebb indokolás helyett utalunk az 1959. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulójának 1. feladatával fennálló hasonlóságra, lásd K. M. L. XIX. kötet 4. o. (1959 szeptember).