Feladat: 1019. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bencsik I. ,  Biborka T. ,  Bollobás B. ,  Csikor F. ,  Csizy L. ,  Frint G. ,  Fritz J. ,  Grüner Gy. ,  Kardeván P. ,  Kóta G. ,  Krámli A. ,  Náray Szabó G. ,  Rátkai János ,  Szegő K. 
Füzet: 1961/március, 116 - 118. oldal  PDF  |  MathML 
Témakör(ök): Műveletek helyvektorok koordinátáival, Egyenesek egyenlete, Feladat
Hivatkozás(ok):Feladatok: 1960/január: 1019. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha K mindkét koordinátája egész szám: (a,b), akkor bármely a K körül írt és egy további R (c,d) rácsponton átmenő k körön általában 8, de legalább 4 rácspont van (1. ábra).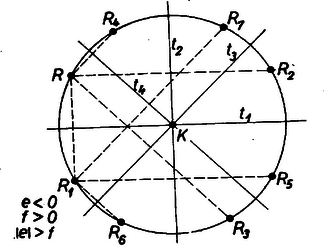

 
 
1. ábra
 

Ha ugyanis bármely rácsponton át párhuzamost húzunk az X, Y-tengellyel, valamint az I és II síknegyedbeli szögfelezőikkel, akkor e t1, t2, t3, t4 egyenesek bármelyikére tükrözve a sík minden pontját a rácspontok tükörképe is rácspont lesz. ‐ Ha c-a=e és d-b=f, vagyis R így is írható: R(a+e,b+f), akkor R tükörképe t1, t2, t4-re rendre R1(a+e,b-f), R2(a-e,b+f), R3(a+f,b+e), R4(a-f,b-e), továbbá R1 tükörképe t2, t3, t4-re R5(a-e,b-f), R6(a-f,b+e), R7(a+f,b-e), és ezek mindegyike rácspont, mert koordinátáik egészek, és a tükrözések folytán valamennyinek K-tól való távolsága a KR távolsággal egyenlő. Az R, R1, ..., R7 pontok csak akkor különbözők, ha e és f abszolút értéke egymástól és 0-tól különböző. Ha e és f egyike 0, vagy ha |e|=|f|≠0, akkor a pontok páronként egybeesnek (e=f=0 lehetetlen, mert K és R különbözők).
Ha K egyik koordinátája, pl. abszcisszája a egész, ordinátája pedig tetszés szerinti β valós szám, akkor legyen egy tetszés szerinti rácspont, amelynek abszcisszája kisebb, mint K-é, R(c,d), ahol c<a. Így a K körül írt KR sugarú kör átmegy R-nek az x=a rácsegyenesre (az előbbi t2-re) való, és R-től különböző R2(2a-c,d) tükörképén, amely szintén rácspont. Hasonlóan látható be az állítás helyessége, ha K abszcisszája valós és ordinátája egész szám.
Legyenek végül K koordinátái (tovább egyszerűsíthetetlen alakú) törtek: p/q és s/t, ahol p és s a 0-tól különböző egészek, q és t 1-nél nagyobb egészek, továbbá p és q, valamint s és t relatív prímek (2. ábra).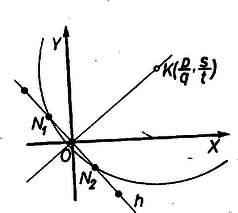
 
 
2. ábra
 

Az állítás igazolására elegendő megmutatnunk, hogy bármely F rácsponthoz megadható olyan K középpontú kör, melyben az F-en átmenő és KF-re merőleges h húr végpontjai rácspontok. Válasszuk F-nek az O origót. Ekkor a KO egyenes és a rá merőleges egyenes iránytangense qs/pt, ill. ‐ pt/qs, ennélfogva h egyenlete y=-ptx/qs, másképpen ptx+qsy=0. Ezen az egyenesen bármely egész j esetén rajta van a (jqs,-jpt) rácspont, mert koordinátái kielégítik az egyenletet. A j=n és j=-n értékekhez tartozó N1(nqs,-npt) és N2(-nqs,npt) pontok egymás tükörképei O-ra (mint fentebb pl. R és R5), és így a KO tengelyre is, ezért a K körül KN1 sugárral írt kör átmegy N2-n is.
A legutóbbi meggondolás az előbbi két esetben is használható, ha F gyanánt olyan rácspontot veszünk, amelynek sem abszcisszája, sem ordinátája nem egyenlő K megfelelő koordinátájával.
Ezzel az állításnál többet bizonyítottunk be, ti. azt, hogy minden racionális koordinátákkal bíró K pont körül számtalan sok olyan kör írható, amelynek kerületén legalább két rácspont van. Ugyanis a fenti meggondolásban az n (pozitív) egész számot számtalan sokféleképpen választhatjuk, és más n esetén mindig más kört kapunk.
 

Rátkai János (Kisújszállás, Móricz Zs. g. III. o. t.)
 

Megjegyzések. 1. Más utakon is lehet racionális koordinátájú pont körüli, több rácsponton átmenő kört találni.
2. Könnyű belátni azt is, hogy a KO egyenesen is számtalan sok rácspont van. Ha F gyanánt ilyet választunk, megeshet, hogy korábban már szerepelt kört kapunk. Emiatt nem volna helyes a legutóbbi állításban ebből indulni ki: ,,F-et és n-et számtalan sokféleképpen választhatjuk''. Azért sem volna ez helyes, mert más F-et választva más h egyenes adódik.
3. Egy dolgozat a 971. feladatra hivatkozva ezt állítja: ,,A tétel megfordítható: ha egy kör kerületén legalább két rácspont van, akkor a középpont koordinátái racionális számok''. Ez helytelen, a fenti K(α,β) esetben β lehet irracionális, pl. a (0,2) középpont körül 3 sugárral írt kör átmegy az (1, 0) és (-1, 0) rácspontokon.
4. Több dolgozat ,,racionális számon'' csak törtet értett.