Kezdőlap


Feladat:	1018. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Bencsik I. , Biborka T. , Bollobás B. , Durst I. , Dömötör Gy. , Farkas Z. , Fejes L. , Fekete J. , Frint G. , Fritz J. , Gagyi Pálffy A. , Gálfi l. , Gazsi L. , Grüner Gy. , Hahn J. , Hajna J. , Hanyi Zs. , Hegedűs I. , Holop A. , Homitzky L. , Jahn A. , Kardeván P. , Kiss A. , Klimó J. , Knuth E. , Krámli A. , Máté A. , Meleghegyi L. , Miklóssy E. , Molnár E. , Nováky Antal , Nováky B. , Pósch Margit , Szegő K. , Székely J. , Szidarovszky Ágnes , Szoboszlai L. , Tihanyi A. , Várady G.
Füzet:	1960/november, 129 - 132. oldal		PDF \| MathML
Témakör(ök):	Egyenletek, Numerikus és grafikus módszerek, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1960/január: 1018. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alkotórészek szokásos jelöléseivel a háromszög és a körcikk területe

\begin{matrix} t_{1} = \frac{1}{2} a b sin γ = \frac{1}{2} \frac{m_{c}}{sin β} \cdot \frac{m_{c}}{sin α} sin γ = \frac{m_{c}^{2} sin γ}{2 sin α sin β}, és t_{2} = \frac{m_{c}^{2} γ}{2} \end{matrix}

ahol

t_{2}

-ben

γ

abszolút mértékben (radiánban) értendő. Így a

t_{2} = t_{1} / 2

követelményből ekvivalens átalakításokkal (ugyanis

sin α

és

sin β

egyike sem 0)

\begin{matrix} 2 γ sin α sin β = sin γ . \end{matrix}

(1)

I. Az I. feltételben említett derékszög megválasztására két különböző lehetőség van: vagy

γ = π / 2

, vagy

α

és

β

közül az egyik, nem lényeges, hogy melyik.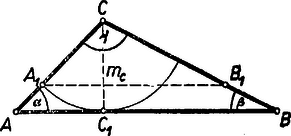

1. ábra

1. eset.

γ = π / 2

esetén

α

és

β

pótszögek, ezért

sin β = cos α

, tehát (1) így alakul:

\begin{matrix} sin 2 α = 2 / π, és innen α \approx 19^{\circ} 46' . \end{matrix}

(A második megoldás ennek pótszöge, ugyanarra a háromszög alakra vezet.) A háromszög szögei:

\begin{matrix} I_{1} : 19^{\circ} 46', 70^{\circ} 14', 90^{\circ} . \end{matrix}

2. eset.

α = π / 2

esetén

β

és

γ

pótszögek,

sin β = cos γ

, ezek alapján (1) így alakul:

\begin{matrix} γ = \frac{1}{2} tg γ \end{matrix}

(2)

Ennek az egyenletnek keressük hegyesszög megoldását. E célból ábrázoljuk a

0 < γ < π / 2

intervallumban az

y_{1} = γ

és

y_{2} = (tg γ) / 2

fügvényeket (2. ábra).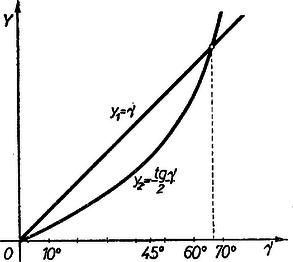

2. ábra

Mindkettő grafikonja az origóból indul, az első meredekebben, mint a második. Az első vonal

45^{\circ}

-os egyenes, a második egyre erősebben növekszik és

γ = π / 2

közelében felvesz tetszőleges nagy értéket. Így a két vonalnak egy metszéspontja, tehát a (2) egyenletnek egy a feladatnak megfelelő megoldása van. Ezt a megoldást rendszeres próbálgatással határozzuk meg közelítőleg.
A grafikon szerint

67^{\circ}

körüli abszcisszánál van a két vonal metszéspontja, ezt vesszük első közelítő értéknek. A

\begin{matrix} γ_{1} = 67^{\circ} \approx 1, 169 értéknél 0, 5 tg γ_{1} \approx 1, 178, \end{matrix}

vagyis (2) jobb oldala nagyobb. Így a grafikonok figyelembevételével (2) gyöke

67^{\circ}

-nál kisebb lesz. Újabb közelítésül

0, 5^{\circ}

-kal kisebb

γ_{2}

szöget választva

\begin{matrix} γ_{2} = 66, 5^{\circ} \approx 1, 161, itt 0, 5 tg γ_{2} \approx 1, 150 < γ_{2}, \end{matrix}

tehát ennél nagyobb értéket kell keresnünk.
A ,,Függvénytáblázatok'' szerint

y = tg x

γ_{2}

és

γ_{1}

között majdnem egyenletesen növekszik, ugyanis változása

0, 1^{\circ}

-onkint

\begin{matrix} 2, 311 - 2, 300 = 2, 322 - 2, 311 = 2, 333 - 2, 322 = 2, 344 - 2, 333 = 0, 011 \end{matrix}

és

\begin{matrix} 2, 356 - 2, 344 = 0, 012. \end{matrix}

Így grafikonjának e rövid szakasza alig tér el az egyenestől, ennek alapján a harmadik közelítő értéket kereshetjük a lineáris interpoláció visszafordításával, annál is inkább, mert percnyi pontosságra törekedve

tg γ

értékét is interpolációval kell képeznünk. Tekintsük (2) átrendezett alakja jobb és bal oldalának

\begin{matrix} Δ = tg γ - 2 γ \end{matrix}

(3)

különbségét.

γ_{2}

esetében

Δ_{2} \approx 2, 300 - 2, 321 = - 0, 021

. Hasonlóan

Δ_{1} \approx 2, 356 - 2, 339 = + 0, 017

. Eszerint míg a szög

γ_{2}

-től

γ_{1}

-ig, vagyis

0^{\circ} 30'

-et nő, addig

Δ

növekedése

0, 017 - (- 0, 021) = 0, 038

. Mi azt keressük, mekkora

δ

értékkel növeljük

γ_{2}

-t, hogy

Δ = 0

legyen, vagyis

- 0, 021

-hez képest

0, 021

-del növekedjék. Eszerint

\begin{matrix} δ : 30' = 0, 021 : 0, 038, innen δ \approx 17' . \end{matrix}

Valóban a

γ_{3} = γ_{2} + δ \approx 66^{\circ} 47' \approx 1, 1656

értékkel

tg γ \approx 2 γ \approx 2, 331

. Eszerint ezen háromszög szögei:

\begin{matrix} I_{2} : α = 90^{\circ}, β \approx 23^{\circ} 13', γ \approx 66^{\circ} 47' . \end{matrix}

II. A háromszög két szögének a II. követelményben szereplő egyenlősége ugyancsak kétféleképpen lehetséges: a kiemelt szerepet játszó

γ

különbözik a másik két szögtől, tehát

α = β

, ill. egyikkel egyenlő, pl.

α = γ

.
1. eset.

α = β = (180^{\circ} - γ) / 2

esetén

sin α = sin β = cos γ / 2

, ezért (1) így alakítható

\begin{matrix} \frac{γ}{2} = \frac{sin γ}{4 sin α sin β} = \frac{2 sin \frac{γ}{2} cos \frac{γ}{2}}{4 cos^{2} \frac{γ}{2}} = \frac{1}{2} tg \frac{γ}{2} . \end{matrix}

Ez a

γ / 2 = ε

ismeretlenre a (2)-vel azonos egyenlet, tehát megoldása

ε \approx 66^{\circ} 47'

, és így a szögek:

\begin{matrix} {II}_{1} : γ \approx 133^{\circ} 34', α = β \approx 23^{\circ} 13' . \end{matrix}

(A fenti két egyenlet megfelelése az 1. ábra szemléletéből is nyilvánvaló, mert, ilyenkor

C C_{1}

két egybevágó,

C_{1}

-nél derékszögű háromszögre vágja

A B C

-t, és így mindkettőben teljesülnie kell az I. 2. eset követelményeinek.)
2. eset.

α = γ

folytán

β = 180^{\circ} - 2 γ

, tehát (1)-ből

sin γ \neq 0

figyelembevételével majd

2 γ = x

jelöléssel

\begin{matrix} 2 γ sin 2 γ = 1, ill. sin x = \frac{1}{x} . \end{matrix}

(4)

Itt tehát első közelítő értéket ismét két jól ismert grafikon:

y_{3} = sin x

és

y_{4} = 1 / x

metszéséből kereshetünk.

γ

hegyesszög, tehát

y_{3}

számára a

0 < x < 180^{\circ} = π

intervallum jön szóba,

y_{4}

számára viszont elég, ha

x \geq 1

, mert (4) bal oldala nem nagyobb 1-nél.

3. ábra

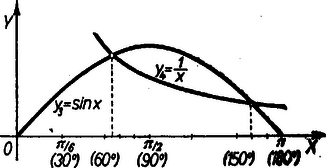A 3. ábra szerint két metszéspont van:

64^{\circ}

és

160^{\circ}

körül. Ezeket a fentihez hasonlóan ,,kifinomítva'' a megfelelő háromszögek szögei

x \approx 63^{\circ} 50'

-ből, ill.

x \approx 158^{\circ} 52'

-ből:

\begin{matrix} {II}_{2,1} : γ & = α \approx 31^{\circ} 55', β \approx 116^{\circ} 10', \\ {II}_{2,2} : γ & = α \approx 79^{\circ} 26', β \approx 21^{\circ} 8' . \end{matrix}

III. A háromszög területét kétféleképpen felező vonalak hosszának összehasonlításához fejezzük ki

t_{1}

-et

m_{c}

-vel és

c

-vel,

t_{2}

-t pedig az

m_{c}

sugárral és az

i

ívvel:

\begin{matrix} 2 t_{1} = m_{c} c, 2 t_{2} = m_{c} i, \end{matrix}

és így

\begin{matrix} t_{2} / t_{1} = 1 / 2 -ből i = c / 2. \end{matrix}

(5)

Legyen másrészt az

A B C

háromszög területét felező, az

A B

-vel párhuzamos szakasz

A_{1} B_{1}

. Így az

A_{1} B_{1} C

háromszög hasonló

A B C

-höz. Területét

t'_{1}

-vel jelölve a követelmény, illetőleg ismert tétel szerint

\begin{matrix} t'_{1} : t_{1} = 1 : 2 és t'_{1} : t_{1} = A_{1} B_{1}^{2} : A B^{2}, \end{matrix}

ennélfogva

A_{1} B_{1} = A B / \sqrt[]{2} = c / \sqrt[]{2}

. Ezt (5)-tel összehasonlítva:

A_{1} B_{1} / i = \sqrt[]{2}

, vagyis a területet felező,

A B

-vel párhuzamos szakasz minden adódott háromszögben hosszabb az ívnél, elég jelentősen: annak több mint

40 %

-ával.

Nováky Antal (Budapest, I. István g. IV. o. t.)

Megjegyzés. Legutóbbi megállapításunk természetesen csak az olyan háromszögekre érvényes, amelyekben a területfelező ív középpontja az egyik csúcs, és az ív érinti a szemben fekvő oldalt.