Kezdőlap


Feladat:	1015. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Biborka T. , Bollobás B. , Bornes Klára , Börzsönyi J. , Fekete J. , Frint G. , Fritz J. , Gazsi L. , Grüner Gy. , Hahn J. , Hajna János , Holop A. , Kiss A. , Klimó János , Knuth E. , Mészáros Kornélia , Molnár E. , Tihanyi A. , Török P. , Várady G. , Veress Gy.
Füzet:	1960/november, 124 - 126. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Trapézok, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1959/december: 1015. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1014. feladat jelöléseivel $G$ oldallapjainak magassága $E M_{2} = a \sqrt[]{5} / 2$ , és így területe $t = a^{2} \sqrt[]{5} / 4$ , az oldalél hossza pedig hasonlóan 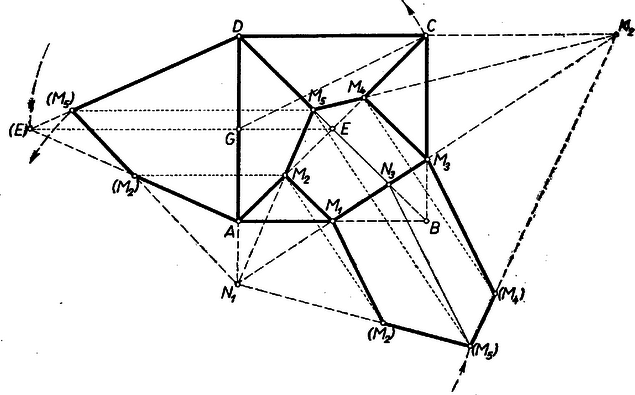$A E = c = a \sqrt[]{6} / 2$ .

Az oldallapokon a metszéssel előállt kisebb háromszögek területét egyszerűen kapjuk a következő nyilvánvaló segédtétel alapján. Ha az

X Y

X Z

fél egyeneseken

Y_{1}

Z_{1}

olyan pontok, amelyekre

X Y_{1} : X Y = λ

és

X Z_{1} : X Z = λ_{1}

, akkor az

X Y_{1} Z_{1}

háromszög területe

λ λ_{1}

-szerese az

X Y Z

háromszög területének. Így az

A B E

oldallap

T_{1}

-re eső

A M_{2} M_{1}

háromszögének területe

t / 2 \cdot 2 = t / 4

, ennélfogva a

T_{2}

-re eső

B E M_{1} M_{2}

rész területe

3 t / 4

. Hasonlóan a

B C E

C D E

D A E

oldallapok

T_{1}

, ill.

T_{2}

-re eső részének területe rendre

4 t / 9

és

5 t / 9

14 t / 15

és

t / 15

, végül

9 t / 10

és

t / 10

, így

G

-nek

4 t

palástfelszínéből

T_{1}

-re esik

91 t / 36 = 91 a^{2} \sqrt[]{5} / 144

T_{2}

-re pedig

53 t / 36 = 53 a^{2} \sqrt[]{5} / 144

. Az alaplap megfelelő részeinek területe (lásd 1014-ben)

11 a^{2} / 12

, ill.

a^{2} / 12

.
A

T_{1}

és

T_{2}

mindegyikének lapját adó

M_{1} M_{2} M_{3} M_{4} M_{5} = Q

síkmetszet

M_{1} M_{2} N_{3} M_{5} = Q_{1}

és

M_{5} N_{3} M_{3} M_{4} = Q_{2}

részei trapézok, mert a 966. feladat szerint

M_{1} M_{2}

M_{4} M_{3}

és

M_{5} N_{3}

mindegyike párhuzamos

B E

-vel, és így egymással is.

Q_{1}

és

Q_{2}

magasságainak

h_{1} : h_{2}

aránya nyilván egyenlő az

M_{2} N_{3} : N_{3} M_{3}

aránnyal; ez pedig a háromszög szögfelezője által létesített szakaszok arányára ismert tétel alapján egyenlő az

M_{2} B : B M_{3}

aránnyal, ugyanis

B N_{3}

, mint az alapnégyzet

B D

átlójának része, felezi az

M_{2} B M_{3}

háromszög

B

-nél levő szögét. Az adatok szerint

M_{2} B : B M_{3} = 3 / 2

, tehát

h_{1} : h_{2} = 3 / 2

Q_{1}

és

Q_{2}

párhuzamos oldalainak hossza

M_{1} M_{2} = m_{1} = c / 2

M_{4} M_{3} = 2 c / 3

és

M_{5} N_{3} = m_{6} = 4 c / 5

, így a középvonal hossza

Q_{1}

-ben

k_{1} = 13 c / 20

Q_{2}

-ben

k_{2} = 11 c / 15

, és ebből arányuk

k_{1} : k_{2} = 39 / 44

.
Ezek szerint

Q

területének megállapítása céljára elég

Q_{1}

és

Q_{2}

-nek

t_{1} = k_{1} h_{1}

, ill.

t_{2} = k_{2} h_{2}

területe közül egyiket kiszámítani, mert a másik a

\begin{matrix} \frac{t_{1}}{t_{2}} = \frac{k_{1} h_{1}}{k_{2} h_{2}} = \frac{k_{1}}{k_{2}} \cdot \frac{h_{1}}{h_{2}} = \frac{39}{44} \cdot \frac{3}{2} = \frac{117}{88} \end{matrix}

arány alapján kifejezhető. Innen

Q

területe

t_{1} + t_{2} = 205 t_{1} / 117

t_{1}

kiszámításához elegendő, ha még meghatározzuk

M_{2} N_{3}

és

M_{1} M_{5}

szárait. Az eddigiekből nyilván

M_{2} N_{3} = 3 M_{2} M_{3} / (3 + 2) = a \sqrt[]{13} / 10

, mert

M_{2} M_{3} = a \sqrt[]{13} / 6

. ‐

M_{1} M_{5}

-öt tekintsük azon téglatest egyik testátlójának, melynek 2 lapsíkja párhuzamos

A B C D

síkjával, további 2‐2 lapsíkja merőleges

A B

-re, ill.

A D

-re, és mindhárom párhuzamos síkpár egyik tagja

M_{1}

-en, másik tagja

M_{5}

-ön megy át. Az

A B C D

-vel párhuzamos síkok távolsága, a téglatest egyik éle, nyilván

M_{1}

és

M_{5}

magasságkülönbségével egyenlő, ami az idézett eredmények ill. adat szerint

4 a / 5 - a / 2 = 3 a / 10

. A további két síkpár távolsága ‐ gondolva

E

M_{1}

M_{5}

-nek

A B

-re, ill.

A D

-re vett vetületére, melyek közül

E

vetülete felezi az illető élt ‐

\begin{matrix} \frac{1}{2} \cdot \frac{a}{2} - \frac{1}{5} \cdot \frac{a}{2} = \frac{3}{10} \cdot \frac{a}{2} = \frac{3 a}{20}, ill. \frac{a}{4} + \frac{a}{10} = \frac{7 a}{20} . \end{matrix}

Ezekkel

\begin{matrix} M_{1} M_{5} = \sqrt[]{{(\frac{3 a}{10})}^{2} + {(\frac{3 a}{20})}^{2} + {(\frac{7 a}{20})}^{2}} = \frac{a \sqrt[]{94}}{20} . \end{matrix}

Messe most már

M_{5} N_{3}

-at az

M_{1}

-en át

M_{2} N_{3}

-mal húzott párhuzamos

N

-ben (1014. fd. 1. ábra), tehát a fentiekből

M_{5} N = m_{6} - m_{1} = 3 c / 10 = 3 a \sqrt[]{6} / 20 = a \sqrt[]{54} / 20

, másrészt

M_{1} N = M_{2} N_{3} = a \sqrt[]{13} / 10 = a \sqrt[]{52} / 20

. Vegyük észre, hogy az

M_{1} M_{5} N

háromszög oldalai arányosak

\sqrt[]{94}

\sqrt[]{54}

\sqrt[]{52}

-vel. Az ezekkel mint oldalakkal szerkesztett háromszög területe a Heron-képlet beszorzással előálló

\begin{matrix} 16 t^{2} = 2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - (a^{4} + b^{4} + c^{4}) \end{matrix}

alakjából

\sqrt[]{11088} / 4 = \sqrt[]{144 \cdot 77} / 4 = 3 \sqrt[]{77}

. Ezért az

M_{1} M_{5} N

háromszög területe

3 a^{2} \sqrt[]{77} / 400

, és így az

M_{5} N

alaphoz tartozó magassága

h_{1} = a \sqrt[]{77} / 10 \sqrt[]{6}

. És mivel

k_{1} = 13 c / 20 = 13 a \sqrt[]{6} / 40

, azért a

Q

síkmetszet területe:

\begin{matrix} \frac{205 t_{1}}{117} = \frac{205 k_{1} h_{1}}{117} = \frac{41 a^{2} \sqrt[]{77}}{720} \approx 0, 4996 a^{2} . \end{matrix}

Mindezek alapján

T_{1}

és

T_{2}

felszíne

\begin{matrix} F_{1} = \frac{a^{2}}{720} (455 \sqrt[]{5} + 660 + 41 \sqrt[]{77}) \approx 2, 289 a^{2}, \\ F_{2} = \frac{a^{2}}{720} (265 \sqrt[]{5} + 60 + 41 \sqrt[]{77}) \approx 1, 406 a^{2} . \end{matrix}

Hajna János (Pécs, Széchenyi I. g. IV. o. t.)

Megjegyzések. 1. A koszinusz-tétel felhasználásával az

A D E

háromszögből

cos A E D ∢ = (2 c^{2} - a^{2}) / 2 c^{2} = 2 / 3

, és így az

M_{1} E M_{5}

háromszögből rövidebben,

\begin{matrix} M_{1} M_{5} = \frac{c^{2}}{4} + \frac{c^{2}}{25} - 2 \frac{c}{2} \cdot \frac{c}{5} \cdot \frac{2}{3} = \frac{47 c^{2}}{300} = \frac{47 a^{2}}{200} . \end{matrix}

Hasonlóan az

A C E

és

M_{1} M_{4} E

háromszögekből ez az egyszerű eredmény adódik:

M_{1} M_{4} = a \sqrt[]{6} / 4 = c / 2 = M_{1} M_{2}

Klimó János (Kaposvár, közg. techn. IV. o. t.)

Q

területét úgy is megkaphatjuk, hogy az

N_{1} N_{2} M_{5}

háromszög területéből kivonjuk az

N_{1} M_{2} M_{1}

és

N_{2} M_{3} M_{4}

háromszögek területének összegét. Vázoljuk ezt a számítási lehetőséget.
A

D N_{1} N_{2}

háromszögből

N_{1} N_{2}^{2} = 52 a^{2} / 9

; az oldallapoknak az alapélen levő szögére

cos A D E ∢ = a / 2 c = 1 / \sqrt[]{6}

; így

N_{1} D M_{5}

-ből (vagy ismét a térbeli Püthagorász-tétellel)

N_{1} M_{5}^{2} = 376 a^{2} / 225

N_{2} D M_{5}

-ből

N_{2} M_{5}^{2} = 84 a^{2} / 25

, így

N_{1} N_{2} M_{5}

területe

2 a^{2} \sqrt[]{77} / 15

(Heron).
A levágandó

N_{1} M_{2} M_{1}

háromszög hasonló

N_{1} N_{3} M_{5}

-höz,

N_{2} M_{3} M_{4}

pedig

N_{2} N_{3} M_{5}

-höz,

N_{1} N_{3} : N_{1} M_{2} = 8 : 5

N_{2} N_{3} : N_{2} M_{3} = 6 : 5

, így

M_{1} N_{1} = 5 M_{5} N_{1} / 8

M_{4} N_{2} = 5 M_{5} N_{2} / 6

, továbbá

M_{2} N_{1} = N_{1} N_{2} / 4

M_{3} N_{2} = N_{1} N_{2} / 2

. Ezekből fenti segédtételünk alapján a levágandó háromszögek területe

5 / 32

, ill.

5 / 12

része

N_{1} N_{2} M_{5}

területének, együtt

55 / 96

része, tehát

Q

-ra

41 / 96

rész marad vissza, ami ismét

41 a^{2} \sqrt[]{77} / 720

.
3. Elsősorban az ábrázoló geometriában jártas versenyzőink számára ‐ de valamennyi olvasónknak is ‐ ajánljuk ábránk tanulmányozását. Ezen az alapsíkba (

K_{1}

-be) forgatva látják az

A D E

oldallapot és az

N_{1} N_{2} M_{5}

háromszöget, az utóbbihoz az

A D (E)

-ben adódott

(M_{5})

-at használtuk fel,

(E)

-hez pedig azt, hogy a

G E

oldalmagasság

G E

és

G D

vetületének egyenlősége folytán egyenlő

G C

-vel. ‐ A dolgozatok jórésze több vetítéssel, hosszas meggondolásokkal lényegében hasonló, de hosszabb utakon jutott eredményhez.