Kezdőlap


Feladat:	1014. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Biborka T. , Bollobás Béla , Bornes Klára , Csikor F. , Csizy L. , Czékus L. , Dudás J. , Dömötör Gyula , Farkas H. , Farkas Z. , Fekete J. , Frint Gábor , Fritz J. , Gazsi L. , Grüner Gy. , Hahn J. , Holop A. , Homitzky L. , Klimó J. , Knuth E. , Kóta G. , Kövessi Nóra , Marton Katalin , Máté A. , Máté Zs. , Molnár E. , Náray-Szabó G. , Noszticzius Z. , Pál G. , Páska Cs. , Pósch Margit , Simonovits M. , Szalay G. , Székely J. , Tihanyi A. , Urbán L. , Vámos P. , Várady G.
Füzet:	1960/november, 120 - 124. oldal		PDF \| MathML
Témakör(ök):	Négyszög alapú gúlák, Térfogat, Térgeometriai számítások trigonometria nélkül, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1959/december: 1014. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük az $M_{2} M_{3} C D A M_{1} M_{5} M_{4} = T_{1}$ rész-test térfogatát $V_{1}$ -gyel, az $M_{2} B M_{3} M_{4} M_{5} M_{1} E = T_{2}$ rész-test térfogatát $V_{2}$ -vel. Elég pl. $V_{1}$ -et önállóan kiszámítani, mert $V_{1}$ és $V_{2}$ összege egyenlő az eredeti $A B C D E = G$ gúla $V = a^{3} / 3$ térfogatával, ahol $a$ az alapél és a magasság közös hosszát jelöli.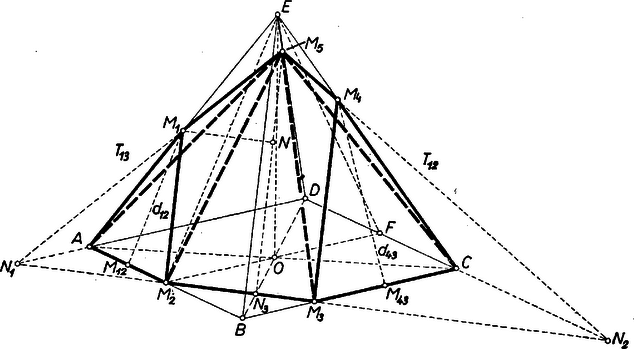

1. ábra

Az ajánlott

M_{5} A M_{2} M_{3} C D = T_{11}

gúla része

T_{1}

-nek, úgy áll elő, hogy

T_{1}

-et egyrészt a

C

M_{3}

M_{5}

, másrészt az

A

M_{2}

M_{5}

csúcsokon átmenő síkkal metsszük. A lemetszett

C M_{3} M_{5} M_{4} = T_{12}

és

A M_{2} M_{5} M_{1} = T_{13}

részek háromoldalú gúlák. Eszerint

V_{1}

-et

T_{11}

T_{12}

és

T_{13}

-nak

V_{11}

V_{12}

V_{13}

térfogatából összeadással kaphatjuk.

T_{11}

alapja az

A B C D

négyzetből a

B M_{3} M_{2}

derékszögű háromszög lemetszésével áll elő, amelyben

B M_{2} = a / 2

B M_{3} = a / 3

, így az alap területe

a^{2} - a^{2} / 12 = 11 a^{2} / 12

T_{11}

magassága az idézett eredmény szerint nyilvánvalóan

4 a / 5

, ennélfogva

V_{11} = 44 a^{3} / 180 = 11 a^{3} / 45

V_{13}

kiszámításához vegyük

T_{13}

alapjának az

A M_{2} M_{1}

háromszöget, ekkor a testmagasság

M_{5}

-nek az

A M_{2} M_{1}

-et tartalmazó

A B E

laptól való

d_{52}

távolsága. Az

A M_{2} M_{1}

lap területének számításához alapnak

A M_{2}

-t véve a magasság

M_{1}

-nek

A M_{2}

-től való

M_{1} M_{12} = d_{12}

távolsága. Így a feltevésre tekintettel

\begin{matrix} V_{13} = \frac{1}{2} A M_{2} \cdot d_{12} \cdot \frac{1}{3} d_{52} = \frac{A M_{2}}{6} \cdot d_{12} d_{52} = \frac{a}{12} \cdot d_{12} \cdot d_{52} . \end{matrix}

(1)

Az idézett eredmények szerint

d_{12}

egyenlő az

A B E

háromszög

E M_{2}

magasságának felével. E magasság hossza nyilván

a \sqrt[]{5} / 2

, tehát

d_{12} = a \sqrt[]{5} / 4

. ‐ Másrészt

d_{52}

annak a távolságnak 5-ödrésze, amennyire

D

(vagy a

D C

él bármely pontja) van az

A B E

laptól. Könnyen számíthatjuk ezt mint a

C D

él

F

felezőpontjának

E M_{2}

-től való távolságát, mert ez az

E M_{2} F

háromszög

F

-ből húzott magassága. E háromszög

t

területének kétféle kifejezéséből ‐ az alap középpontját

O

-va1 jelölve ‐

\begin{matrix} 5 d_{52} = 2 t / E M_{2} = M_{2} F \cdot E O / E M_{2} = a^{2} / (a \sqrt[]{5} / 2) = 2 a / \sqrt[]{5}, \end{matrix}

ennélfogva

d_{52} = 2 a / 5 \sqrt[]{5}

, és végül

\begin{matrix} V_{13} = \frac{a}{12} \cdot \frac{a \sqrt[]{5}}{4} \cdot \frac{2 a}{5 \sqrt[]{5}} = \frac{a^{3}}{120} . \end{matrix}

Hasonlóan

\begin{matrix} V_{12} = C M_{3} \cdot d_{43} \cdot d_{53} / 6 = d_{43} \cdot d_{53} \cdot a / 9, \end{matrix}

(2)

ahol

d_{43} = M_{4} M_{43}

M_{4}

távolsága

C M_{3}

-tól, és

d_{53}

M_{5}

távolsága a

C M_{3} M_{4}

, azaz

C B E

laptól. Itt nyilván

d_{43} = 2 E M_{2} / 3 = a \sqrt[]{5} / 3

, és

d_{53} = d_{52}

, tehát

\begin{matrix} V_{12} = \frac{a \sqrt[]{5}}{3} \cdot \frac{2 a}{5 \sqrt[]{5}} \cdot \frac{a}{9} = \frac{2 a^{3}}{135} . \end{matrix}

Mindezek alapján

\begin{matrix} V_{1} = V_{11} + V_{12} + V_{13} = a^{3} (\frac{11}{45} + \frac{2}{135} + \frac{1}{120}) = \frac{289 a^{3}}{1080}, \end{matrix}

ebből pedig az előrebocsátottak szerint

\begin{matrix} V_{2} = V - V_{1} = \frac{a^{3}}{3} - \frac{289 a^{3}}{1080} = \frac{71 a^{3}}{1080} . \end{matrix}

(Mint látjuk,

V_{2}

valamivel kisebb

V_{1} / 4

-nél.)

Marton Katalin (Budapest, Fazekas M. gyak. g. IV. o. t.)

Megjegyzések. 1. Az (1) és (2) céljára elég a

d_{12} \cdot d_{52}

, ill.

d_{43} \cdot d_{53}

szorzat értékét

a

-val kifejeznünk. Az utóbbi szorzat megállapítható

G

és

T_{1}

-nek egy a

C B

élre merőleges

K_{2}

síkon adódó vetületéből. E vetületben

d_{43}

és

d_{53}

valódi nagyságukban látszanak, mert mindkét szakasz merőleges

C B

-re és így párhuzamos

K_{2}

-vel. Másrészt egyik oldalát és hozzátartozó magasságát adják az

M_{43}

M_{4}

M_{5}

csúcsok vetületei által alkotott háromszögnek, így szorzatuk e háromszög 2-szeres területét adja. Ez a terület úgy is kiszámítható, hogy összehasonlítjuk annak a háromszögnek a területével, amelyet a

G

test

A

C

E

csúcsainak ugyancsak

K_{2}

-re való vetületei határoznak meg. E háromszög területe,

A C

vetületét véve alapnak,

a^{2} / 2

, mert alapja és magassága

a

. Ha pedig

C E

vetületét vesszük alapnak, ennek

d_{43}

vetülete a 966. feladat idézett eredményei szerint

2 / 3

része, az

A

vetületéből húzott magasságnak pedig az

M_{5}

vetületéből húzott

d_{53}

magasság

1 / 5

része. Eszerint a vetületbeli

M_{43} M_{4} M_{5}

háromszög területe

a^{2} / 15

, a vizsgált szorzat

2 a^{2} / 15

, végül ismét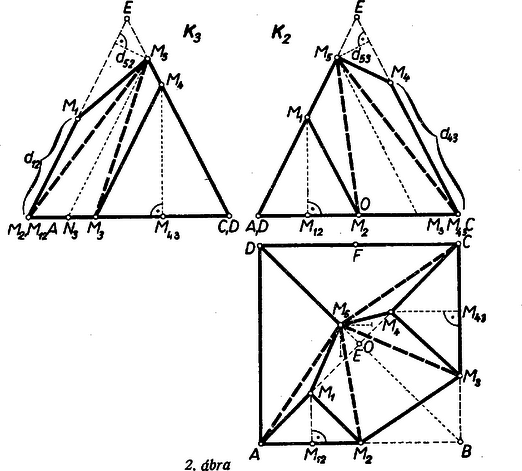

\begin{matrix} V_{12} = (a / 9) \cdot (2 a^{2} / 15) = 2 a^{3} / 135. \end{matrix}

Hasonlóan

G

és

T_{1}

-nek egy az

A C

élre merőleges

K_{3}

síkon előálló vetületéből az idézett eredmények alapján (lásd a 2. ábrát)

\begin{matrix} d_{12} \cdot d_{52} = 2 \cdot \frac{a^{2}}{2} \cdot \frac{1}{2} \cdot \frac{1}{5} = \frac{a^{2}}{10}, és így V_{13} = \frac{a^{3}}{120} . \end{matrix}

2. Ajánljuk olvasóinknak, hogy térbeli feladatok megoldásában próbálják meg segítségül venni az ábrázoló geometria rajzoló módszereivel előállított vetületeket. A fentihez hasonló meggondolásokban, a képeknek az eredeti jelentéstől kissé eltávolodó értelmezésében azonban fokozott óvatosságot tanúsítsunk ! Ilyet látunk a következő megjegyzésben is.
3. Egyrészt a

D N_{3}

szakaszon, másrészt rendre az

M_{1}

M_{5}

M_{4}

ponton át fektetett síkokkal

T_{1}

-et négy részre vágva is kiszámíthatjuk

V_{1}

-et. Az egymás utáni részek: az

N_{3} D A M_{2}

alapú,

M_{1}

csúcsú, négyoldalú gúla, a közös

N_{3} D M_{5}

alapú és

M_{1}

, ill.

M_{4}

csúcsú háromoldalú gúlák és az

N_{3} D C M_{3}

alapú

M_{4}

csúcsú gúla.
Az első és a negyedik gúla alapterülete az 1015. feladat segédtételének felhasználásával

9 a^{2} / 20

, ill.

7 a^{2} / 15

, a megfelelő magasságok

a / 2

, ill.

2 a / 3

, így a térfogatok a

3 a^{3} / 40

, ill.

14 a^{3} / 135

. A 2-ik és 3-ik gúla térfogatának összege egyszerre számítható: a mondott közös alap területe

16 / 25

része a

D B E

háromszög

a^{2} / \sqrt[]{2}

területének:

8 a^{2} \sqrt[]{2} / 25

, a két magasság összege pedig egyenlő az

M_{1} M_{4}

szakasznak a

K_{1}

alapsíkon levő vetületével

5 a \sqrt[]{2} / 12

-vel. Tehát az együttes térfogat

4 a^{3} / 45

. E három térfogat összege a fenti

V_{1}

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

II. megoldás: Részekre bontás nélkül, kiegészítéssel számíthatjuk

V_{1}

-et, ha

T_{1}

-hez hozzávesszük az

A M_{2} N_{1}

alapú,

M_{1}

csúcsú és a

C M_{3} N_{2}

alapú,

M_{4}

csúcsú háromoldalú gúlát. Így a

D N_{1} N_{2}

alapú,

M_{5}

csúcsú háromoldalú gúlához jutunk és

\begin{matrix} V_{1} = \frac{1}{3} \cdot \frac{1}{2} (\frac{4 a}{3} \cdot 2 a \frac{4 a}{5} - \frac{a}{3} \cdot \frac{a}{2} \cdot \frac{a}{2} - \frac{2 a}{3} \cdot a \frac{2 a}{3}) = \frac{289 a^{3}}{1080} . \end{matrix}

Dömötör Gyula (Szeged, Radnóti M. g. III. o. t.)

III. megoldás: Számítsuk ki önállóan

V_{2}

-t abból, hogy

T_{2}

-t az

M_{2} M_{3} E

síkkal metszve két olyan gúlát kapunk, melyek közös csúcsa

E

, alapjuk pedig

M_{2} M_{3} B

és

M_{1} M_{2} M_{3} M_{4} M_{5}

. Ezek területe

a^{2} / 12

, ill. az 1015. feladat megoldása szerint

41 a^{2} \sqrt[]{77} / 720

. Az első gúla magassága

a

, így térfogata

a^{3} / 36

. A második gúla magassága

E

-nek, vagy ami ugyanaz, a

B E

élnek a metsző

S

-től való távolsága. Ennek meghatározására messük

T_{2}

-t a

B E

-re merőleges síkkal. A síkmetszet oldalai egyenlők az

M_{2} M_{1}

és

B E

, a

B E

és

M_{3} M_{4}

, ill. az

M_{2} M_{1}

és

M_{3} M_{4}

párhuzamosok távolságával. Az első nyilván fele, a második pedig harmada az

A B E

háromszögben a

B E

alaphoz tartozó

a \sqrt[]{30} / 6

magasságnak, vagyis

a \sqrt[]{30} / 12

, ill.

a \sqrt[]{30} / 18

; a harmadik pedig az 1015. feladat megoldása szerint

h_{1} + h_{2} = 5 h_{1} / 3 = a \sqrt[]{462} / 36

. Ezekből e metszet területe (a Heron-képlet beszorzással adódó alakjából)

a^{2} \sqrt[]{6} / 36

, és a harmadik oldalhoz tartozó magassága, a keresett távolság

2 a / \sqrt[]{77}

. Most már az

E M_{1} M_{2} M_{3} M_{4} M_{5}

gúla térfogata

41 a^{3} / 1080

és a két gúla térfogatának összege

V_{2} = 71 a^{3} / 1080

Frint Gábor (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

Megjegyzés.

T_{2}

-t az

N_{3} B E M_{5}

síkkal kettévágva két ferdén lemetszett háromoldalú hasábot kapunk. Könnyű belátni, hogy ilyen hasáb térfogatát az oldalélekre merőleges keresztmetszetnek az oldalélek számtani közepével való szorzata adja (pl. a legrövidebb oldalél egyik végpontján át a másik véglappal párhuzamos metszéssel a test egy hasábra és egy trapéz alakú gúlára bontható; másképpen pedig egy trapéz és egy háromszög alapú gúlára). Az

M_{2} B N_{3} M_{5} M_{1} E

hasáb keresztmetszetének területe a

h_{1} : h_{2} = 3 / 2

arány alapján

3 / 5

része a fenti megoldásban nyert

a^{2} \sqrt[]{6} / 36

keresztmetszetnek, a

B M_{3} N_{3} M_{5} E M_{4}

hasábé pedig

2 / 5

része ugyanennek. Így ‐

c

-vel a

B E = a \sqrt[]{6} / 2

oldalélt jelölve

\begin{matrix} V_{2} = \frac{3}{5} \cdot \frac{a^{2} \sqrt[]{6}}{36} \cdot \frac{1}{3} (c + \frac{4 c}{5} + \frac{2 c}{2}) + \frac{2}{5} \cdot \frac{a^{2} \sqrt[]{6}}{36} \frac{1}{3} (c + \frac{4 c}{5} + \frac{2 c}{3}) = \\ = \frac{23 a^{2} c \sqrt[]{6}}{1800} + \frac{37 a^{2} c \sqrt[]{6}}{4050} = \frac{71 a^{2} c \sqrt[]{6}}{3240} = \frac{71 a^{3}}{1080} . \end{matrix}

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)