Kezdőlap


Feladat:	1013. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Biborka T. , Bollobás B. , Fekete J. , Flanek L. , Fritz J. , Gálfi l. , Gazsi L. , Grüner Gy. , Holop A. , Klimó J. , Knuth Előd , Marton Katalin , Máté Attila , Máté Zs. , Pinkert A. , Tomcsányi Gy. , Várady G.
Füzet:	1960/november, 118 - 120. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságvonal, Feuerbach-kör, Trapézok, Húrnégyszögek, Projektív geometria, Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1959/december: 1013. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Kimutatjuk, hogy ha $A_{3}$ létezik, akkor rajta van a háromszög $M$ magasságpontját és a köré írt kör $O$ középpontját összekötő $e$ egyenesen ( $e$ csak szabályos $A B C$ háromszög esetén nem létezik, mert csak ebben esik egybe $O$ és $M$ ). Ezzel már igazoltuk az állítást, mert hasonlóan $B_{3}$ , $C_{3}$ is pontja 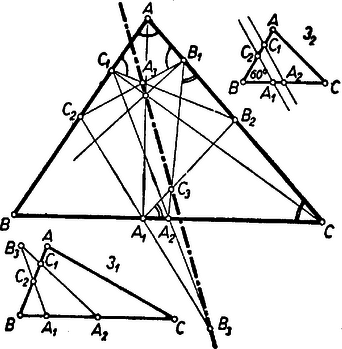$e$ -nek.

1. ábra

Messe az

A_{3}

-on átmenő

A B = c

-re merőleges egyenes

A B

-t

C'

-ben,

e

-t

P

-ben, továbbá az

A_{3}

-on átmenő,

A C = b

-re merőleges egyenes

A C

-t

B'

-ben,

e

-t

Q

-ban 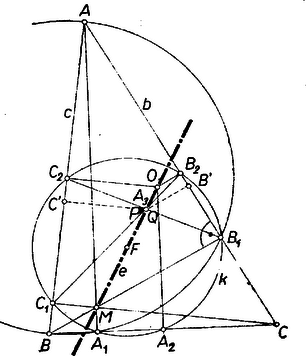(2. ábra).

2. ábra

Azt fogjuk megmutatni, hogy

P

és

Q

egybeesik; ebből következik, hogy azonosak

A_{3}

-mal, mert

c

és

b

nem párhuzamosak.
Minthogy

M

és

O

egyrészt a

c

-re

C_{1}

és

C_{2}

-ben, másrészt a

b

-re

B_{1}

és

B_{2}

-ben emelt merőlegesek metszéspontja, azért a

b

e

egyenespárt 3 párhuzamos egyenes metszi át, így

\begin{matrix} M Q : Q O = B_{1} B' : B' B_{2} . \end{matrix}

(1)

Hasonlóan a

c

e

egyenespáron levő metszetekre

\begin{matrix} M P : P O = C_{1} C' : C' C_{2} . \end{matrix}

(2)

Így azt kell belátnunk, hogy (1) és (2) második arányai egyenlők.
Ehhez felhasználjuk, hogy az

A_{3}

előállításában szereplő

B_{1}

C_{1}

B_{2}

C_{2}

pontok egy körön vannak, éspedig az

A_{2} B_{2} C_{2}

háromszög

k

körülírt körén (az

A B C

háromszög ún. Feuerbach-féle körén). Elég pl.

B_{1}

-re megmutatni, hogy

k

-n van. Valóban, az

A_{2}

B_{2}

B_{1}

C_{1}

csúcsokkal meghatározott konvex négyszög szimmetrikus trapéz, tehát körbe írható. Ugyanis

A_{2} C_{2} ∥ B_{1} B_{2}

, az

A_{2} B_{2}

és

C_{2} B_{1}

szakaszok (vagy mindkettő oldal, vagy mindkettő átló) egyenlők

A B / 2

-vel, ‐

C_{2} B_{1}

azért, mert

B_{1}

rajta van az

A B

átmérő fölötti Thalész-körön, melynek középpontja

C_{2}

‐, végül a négyszög általában nem paralelogramma, mert

B_{1}

általában különbözik

A

és

C

-től, az

A C

egyenes azon két pontjától, amelyek

A_{2}

B_{2}

C_{2}

-t paralelogrammává egészítik ki; ha pedig pl.

B_{1} \equiv C

, akkor a négyszög téglalap és ezért körbe írható.
Eszerint a

B_{1} C_{2}

C_{1} B_{2}

szakaszpár a végpontjaikkal mint csúcsokkal meghatározott konvex húrnégyszögnek vagy a két átlóját adja (ilyen az 1. ábrán

A_{3}

), vagy két szemben fekvő oldalát (ilyen jellegű az 1. ábra

B_{3}

pontja, persze minden

A

betűt

B

-re cserélve és viszont). Ezért az

A_{3} B_{1} B_{2}

és

A_{3} C_{1} C_{2}

háromszögek mindenképpen hasonlók, mert szögeik rendre egyenlők (kerületi szögek, csúcsszögek, közös szögek). Ennélfogva valóban áll

\begin{matrix} B_{1} B' : B' B_{2} = C_{1} C' : C' C_{2}, \end{matrix}

mert hasonló háromszögekben bármely megfelelő szakaszok aránya egyenlő, és itt az

A_{3}

-ban összefutó oldalaknak a szemben levő oldalon levő vetületeiről van szó. Ezzel az állítást általában bebizonyítottuk.
Bizonyításunkat ki kell egészítenünk az olyan esetek vizsgálatával, ha a

B_{1}

B_{2}

és

C_{1}

C_{2}

párok egyike, pl. az első ‐ egybeesik, mert ekkor

A_{3} \equiv B_{2} \equiv B_{1}

A_{3} B_{1} B_{2}

háromszög elfajul ponttá. Így azonban állításunk nyilvánvaló, mert ekkor az

A B C

háromszög egyenlő szárú:

B A = B C

, tehát

e

azonos a szimmetriatengellyel, és így átmegy

A_{3}

-on. Ha pedig

B_{1} \equiv B_{2}

és

C_{1} \equiv C_{2}

akkor

A B C

egyenlő oldalú,

A_{3}

B_{3}

C_{3}

határozatlanok.
Ha a háromszögnek csak egy szöge

60^{\circ}

-os, pl.

α

, vagy ha

α = 120^{\circ}

, akkor ‐ mint az 541. gyakorlatban láttuk ‐

B_{1} C_{2}

és

C_{1} B_{2}

párhuzamosak,

A_{3}

nem létezik. Fenti bizonyításunk szerint

B_{3}

és

C_{3}

ekkor is

e

-n vannak. Megmutatjuk, hogy ilyenkor

B_{1} C_{2}

és

C_{1} B_{2}

párhuzamosak

e

-vel. Feltevésünk folytán

A B_{1} = A B / 2 = A C_{2}

A C_{1} = A C / 2 = A B_{2}

és így

B_{1}

és

C_{2}

, valamint

C_{1}

és

B_{2}

egymásnak tükrös párjai az

α

belső, ill. külső felezőjére, ezért

B_{1} C_{2}

és

C_{1} B_{2}

merőlegesek e felezőre. Másrészt ugyanez áll

e

-re is, mert a

C_{1} A B_{1} M

és

B_{2} A C_{2} O

négyszögek egybevágók, ugyanis 2‐2 megfelelő oldaluk és 3‐3 megfelelő szögük egyenlő, továbbá 3‐3 megfelelő csúcsuk egymásnak fenti szög felezőjére tükrös párja, tehát

M

és

O

is tükrös pár.

Máté Attila (Szeged, Dózsa Gy. ált. isk. VII. o. t)

II. megoldás: Mint az I. megoldásban láttuk, a magasságtalppontok rajta vannak az oldalfelezőpontokkal meghatározott

k

körön. Ha e 6 pontot az

A_{1}

B_{2}

C_{1}

A_{2}

B_{1}

C_{2}

sorrendben tekintjük egy a

k

-ba írt hatszög csúcsainak, akkor a szóban forgó egyenespárok 2‐2 tagja e hatszögnek 2‐2 szembenfekvő oldala. Ezért a kúpszeletbe írt hatszögre vonatkozó Pascal-féle tétel ¹ szerint

A_{3}

B_{3}

C_{3}

metszéspontjaik egy egyenesen vannak.

Knuth Előd (Budapest, I. István g. III. o. t.)

Megjegyzés. A Pascal-tétel alapján a feladat állítását abból is bizonyíthatjuk, hogy

A_{3}

B_{3}

C_{3}

bármelyike, pl. ismét

A_{3}

, rajta van az

M

-et a háromszög

S

súlypontjával összekötő egyenesen. Tekintsük az

A B

A C

egyenespárt elfajult

k'

kúpszeletnek. A

B_{1} B B_{2} C_{1} C C_{2}

hatszög csúcsai

k'

-n vannak, tehát szemben fekvő oldalainak metszéspontjai:

B_{1} B

és

C_{1} C

-nek

M

B B_{2}

és

C C_{2}

-nek

S

, végül

B_{2} C_{1}

, és

C_{2} B_{1}

-nek

A_{3}

‐ egy egyenes pontjai. (Az

M

S

pontokkal meghatározott egyenes azonos a fentebbi

M O

egyenessel, a háromszög Euler-féle egyenesével.)

¹Lásd pl. Schopp János: Kúpszeletek (Középiskolai Szakköri Füzetek), Tankönyvkiadó, 1955, 71. o. ‐ Vigassy Lajos: Síkmértani szerkesztések térmértani megoldássa (Középiskolai Szakköri Füzetek), Tankönyvkiadó, 1957, 33. o.