Kezdőlap


Feladat:	1011. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Grüner Gy. , Hajna János , Hegedüs I. , Homitzky Lajos , Horváth S. , Klimó J. , Máté Zsolt , Molnár Emil , Simonovits Miklós , Tihanyi A. , Várady G.
Füzet:	1960/november, 112 - 117. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Terület, felszín, Trapézok, Szélsőérték-feladatok differenciálszámítás nélkül, Négyszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1959/december: 1011. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A kérdéses trapézokban két szomszédos szög derékszög, a másik kettő általában ferde szög. A kérdést két esetben kellene vizsgálnunk aszerint, hogy az állandó összegű két szomszédos oldal között tetszés szerinti ( $0^{\circ}$ és $180^{\circ}$ közötti) szög, ill. derékszög van, azonban mindkettő speciális esete annak a feladatnak, amely az adott feladatból a ,,derékszögű'' jelző elhagyásával keletkezik. Célszerű ezért előbb ezt az általánosabb feladatot megoldanunk. Tekintsük tehát azokat az a $A B C D = T$ trapézokat, amelyeknek párhuzamos oldalai $A B$ és $C D$ , bennük a $B A$ és $A D$ oldalak összege adott $s$ állandó, továbbá $B A D$ , valamint $A B C$ szögük egy adott $α$ , ill. $β$ szöggel egyenlő.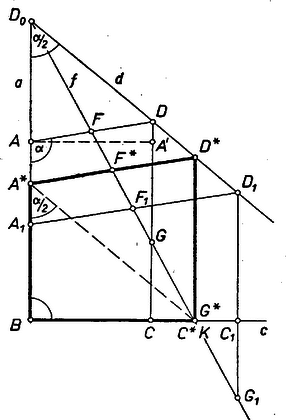
Legyenek a síkon egy $β$ nagyságú szög szárai az $a$ és $c$ félegyenesek. Helyezzük el valamennyi vizsgálandó trapézunkat úgy, hogy $B$ csúcsuk a $β$ szög csúcsába, $A$ , $C$ csúcsaik pedig $a$ , ill. $c$ -re essenek. Forgassuk bele valamennyi trapéz $A D$ oldalát $A$ körül a $B A$ oldal meghosszabbításába; így valamennyi $D$ csúcs az $a$ szár azon $D_{0}$ pontjába jut, amelyre $B D_{0} = s$ (1. ábra).

1. ábra

A D D_{0}

háromszögek egyenlő szárúak, és

D_{0}

-nál levő szögük

α / 2

, állandó, ennélfogva minden

D

csúcs azon a

D_{0}

-ból kiinduló

d

félegyenesen van, amely a

D_{0} B

félegyenessel a

c

-t tartalmazó oldalán

α / 2

szöget zár be.
Avégett, hogy trapézaink területét összehasonlítsuk, próbáljunk mindegyikhez egy olyan vele egyenlő területű trapézt képezni, melyben az egyik alap

D_{0} B

, és egy további csúcs a

c

-n van.

T

-hez ilyen az a

D_{0} B C G = T'

trapéz, amelynek

G

csúcsát az az egyenes metszi ki

D C

-ből, amely az

A D

szár

F

felezőpontját

D_{0}

-lal köti össze, ‐ feltéve, hogy ez a

G

metszéspont a

D C

szakaszra vagy

C

-be esik (egyelőre csak az ilyen

T

-ket tekintjük). Így ugyanis a levágott

F D G

és a hozzávett

F A D_{0}

háromszögek egybevágók, tehát

T'

területe valóban egyenlő

T

-ével.

D_{0} F

D_{0} A D

háromszög

D_{0}

-ból induló súlyvonala. És mivel valamennyi

D_{0} A D

háromszög hasonló helyzetű ‐ hasonlósági pontjuk

D_{0}

‐, azért az

A D

szár minden helyzetének

F

felezőpontja egy a

D_{0}

-on átmenő

f

egyenesen van rajta. Legyen

f

és

c

metszéspontja

K

. Így mindegyik tekintetbe vett

T

D_{0} B K = H

háromszögnek része, nyilvánvaló tehát, hogy annak a

T^{*}

-nak a területe a legnagyobb, amelyben

G

és

C

K

-ba esik, és

T^{*}

területe egyenlő

H

területével.
Azon további

T

-k területéről, melyeknek

D C

oldalát

f

C

-n túli meghosszabbításban metszi, vagyis

K

-n túl (az 1. ábrán pl.

A_{1} B C_{1} D_{1}

), nyilvánvaló, hogy kisebb

H

területénél, éspedig annyival, amennyi a

K C_{1} G_{1}

háromszög területe. Ennyivel kisebb ugyanis a

T

-ből az

F_{1} K

szakasszal levágott

F_{1} K C_{1} D_{1}

négyszög területe a hozzávett

F_{1} A_{1} D_{0}

háromszög területénél. ‐ Ennélfogva a vizsgálandó trapézok közül

T^{*}

területe a legnagyobb.
Mindezek szerint

T^{*}

-ot az alábbi úton kaphatjuk. Az

a

-n felvett

B D_{0} = s

szakaszhoz

D_{0}

-ban meghúzzuk a vele

α / 2

szöget bezáró

d

-t és

B

-ben a

β

szöget bezáró

c

-t. A

D_{0} B

-n tetszés szerint választott

A

körül

A D_{0}

sugárral

d

-ből kimetsszük

D

-t, a

D_{0} A D

háromszöget kiegészítjük

D_{0} A G D

paralelogrammává, majd ennek

D_{0} G

átlójával

c

-ből kimetsszük

K \equiv C^{*}

-ot. Végül

C^{*}

-on át

a

-val, ill.

d

-vel párhuzamost húzva kimetsszük

d

-ből

D^{*}

-ot,

a

-ból

A^{*}

-ot.
A

D_{0} A^{*} C^{*} D^{*}

paralelogramma hasonló

D_{0} A G D

-hez, ezért a

D_{0} A^{*} D^{*}

háromszög hasonló

D_{0} A D

-hez, vagyis egyenlő szárú, tehát egyrészt

A^{*} D^{*} = A^{*} D_{0}

, és így

B A^{*} + A^{*} D^{*} = B D_{0} = s

, másrészt

B A^{*} D^{*} ∢ = A^{*} D_{0} D^{*} ∢ + A^{*} D^{*} D_{0} ∢ = α

, ezek szerint

T^{*}

megfelel a követelményeknek.

K

egyértelműen létrejön, ha

β

és a

B D_{0} F = δ

szög összege kisebb

180^{\circ}

-nál. Továbbá az előálló

T^{*}

megfelelő, ha

A^{*}

B D_{0}

szakaszra esik, ennek feltétele a

B K A^{*}

háromszögből:

β + α / 2 < 180^{\circ}

. Az utóbbi feltétel

K

létrejövéséhez is elegendő, mert

δ

α / 2

-nek része, tehát kisebb annál.
Ezek szerint speciálisan

β = 90^{\circ}

-kal és tetszés szerinti

0^{\circ}

és

180^{\circ}

közti

α

-val feladatunk megoldható, mert

α / 2

hegyesszög (ilyen eset az 1. ábra).
Ha viszont

α = 90^{\circ}

, akkor a

β + 45^{\circ} < 180^{\circ}

feltétel alapján a fentiek szerint csak

β < 135^{\circ}

esetére kapunk megoldást.

β = 135^{\circ}

esetében

A^{*}

B

-be esik, a trapéz elfajul egyenlő szárú derékszögű háromszöggé és az előírt

β

szög az idomban nem látható.
A

β \geq 135^{\circ}

esetekre megmutatjuk, hogy nincs legnagyobb területű valódi trapéz, mert ha

B A_{1} D_{1} C_{1} = T_{1}

és

B A_{2} D_{2} C_{2} = T_{2}

(2. ábra) teljesítik a követelményeket és

B A_{2} < B A_{1}

, akkor

T_{2}

területe nagyobb

T_{1}

területénél, vagyis a terület a

B A

oldal csökkenésével nő.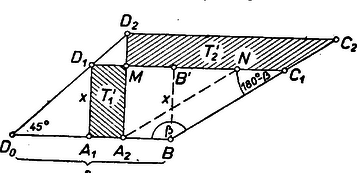

2. ábra

Legyen

D_{1} C_{1}

és

A_{2} D_{2}

metszéspontja

M

, és messe az

A_{2}

-n át

B C_{1}

-gyel húzott párhuzamos

D_{1} C_{1}

-et

N

-ben. Így egyrészt

A_{2} A_{1} = (B A_{1} + A_{1} D_{1}) - (B A_{2} + A_{1} D_{1}) = (B A_{2} + A_{2} D_{2}) - (B A_{2} + A_{2} M) = M D_{2}

, vagyis

T_{1}

és

T_{2}

nem közös részeiben, az

A_{1} A_{2} M D_{1} = T'_{1}

téglalapban és az

M C_{1} C_{2} D_{2} = T_{2}'

trapézban az egyik oldal, ill. a magasság egyenlő. Másrészt az

A_{2} N M

derékszögű háromszögben

A_{2} N M ∢ = 180^{\circ} - β \leq 45^{\circ} \leq β - 90^{\circ} = N A_{2} M ∢

, így

A_{2} M \leq M N < M C_{1} < D_{2} C_{2}

, tehát

T_{2}'

területe nagyobb

T_{1}'

területénél, amit bizonyítani akartunk. ‐ Ezzel vizsgálatunkat befejeztük.

Összeállítva Molnár Emil (Győr, Révai M. g. III. o. t.),

Simonovits Miklós (Budapest, Radnóti M. g. II. o. t.)

és Hornitzky Lajos (Budapest, I. István g. III. o. t.)

dolgozataiból és diszkusszióval kiegészítve.

Valamennyi többi dolgozat számítással, legnagyobbrészt trigonometriai számítással készíti elő a szerkesztést. Ilyen a következő megoldás.

II. megoldás: 1. Legyen a derékszögű szár ismét

B C

, és

B A D ∢ = α

B A + A D = s

. A szerkesztés előkészítéséül

α

-ból és

s

-ből számítással állapítjuk meg a legnagyobb területtel bíró trapéz

A D = x

,,ferde'' szárát. Nyilván csak a

0 < x < s

értékekről lehet szó. ‐

A

-nak

D C

-n levő vetületét

A'

-vel jelölve

D C = A' C - D A' = A B - D A'

, ha

α

hegyesszög, és

D C = A B + D A'

, ha

α

tompaszög (1. ábra). Mivel

D A'

hosszát a

D A cos α = x cos α

szorzat abszolút értéke adja, és

cos α

hegyes és tompa szögekre ellentett jelű, azért a két kifejezést egybefoglalhatjuk:

\begin{matrix} D C = A B - x cos α = (s - x) - x cos α = s - x (1 + cos α) . \end{matrix}

Ennélfogva a trapéz középvonala

s - x - (x cos α) / 2 = s - (2 + cos α) x / 2

. Másrészt a magasság

A A' = x sin α

, és így a terület:

\begin{matrix} t = [s x - (2 + cos α) x^{2} / 2] sin α . \end{matrix}

Mivel a

sin α

tényező pozitív állandó, elég megkeresni a

\begin{matrix} \frac{t}{sin α} = y_{1} = s x - \frac{1}{2} (2 + cos α) x^{2} \end{matrix}

(1)

függvény legnagyobb értékét, ha

0 < x < s

y_{1}

x

-nek másodfokú függvénye, mert

x^{2}

együtthatója bármely

α

esetén 0-tól különböző, éspedig negatív, hiszen

cos α > - 1

. Ennek kiemelésével és teljes négyzetté kiegészítéssel (1) az

\begin{matrix} y_{1} & = - \frac{1}{2} (2 + cos α) (x^{2} - \frac{2 s}{2 + cos α} x) = \\ = - \frac{1}{2} (2 + cos α [{(x - \frac{s}{2 + cos α})}^{2} - \frac{s^{2}}{{(2 + cos α)}^{2}}] = \\ = - \frac{1}{2} (2 + cos α) {(x - \frac{s}{2 + cos α})}^{2} + \frac{s^{2}}{2 (2 + cos α)} \end{matrix}

alakban írható. Ebben csak az első tag változó, és értéke negatív vagy 0, mert, a kéttagú kifejezés négyzete pozitív vagy 0. Eszerint

y_{1}

-nek van legnagyobb értéke éspedig arra az

x

-re, amelyre a kéttagú értéke 0, vagyis ha

\begin{matrix} x = x^{*} = \frac{s}{2 + cos α} . \end{matrix}

(2)

A szóba jövő

α

értékek mellett

2 + cos α > 1

. Így egyrészt

x^{*} < s

(természetesen

s > 0

), másrészt

x^{*} > 0

, tehát

x^{*}

x

számára figyelembe jövő értékek közé tartozik.
A legnagyobb területű trapéz megszerkesztése során kézenfekvő

x^{*}

-ot pl. (2) alapján hasonló háromszögek felhasználásával előállítani. Vegyük észre azonban, hogy a keresett trapézben a fenti kifejezések és (2) alapján

D C = s - s (1 +

+ cos α) / (2 + cos α) = s / (2 + cos α) = x^{*} = A D

, vagyis az

A D C

háromszög egyenlő szárú. Tekintve még, hogy az

A

D

C

csúcsok hasonlóság erejéig meghatározzák

A B C D

-t, adódik a következő szerkesztés. Egy

D_{1}

csúcsú,

180^{\circ} - α

nagyságú szög száraira egyenlő

D_{1} A_{1}

, és

D_{1} C_{1}

szakaszokat mérünk (3. ábra).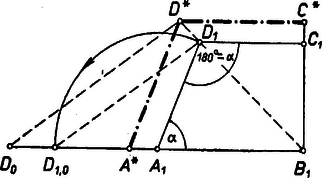

3. ábra

D_{1} C_{1}

-gyel

A_{1}

-en át párhuzamost,

D_{1} C_{1}

-re

C_{1}

-en át merőlegest húzunk, metszéspontjuk

B_{1}

A_{1} D_{1}

-et

A_{1}

körül

B_{1} A_{1}

meghosszabbítására forgatjuk,

D_{1}

új helyzete

D_{1,0}

B_{1}

-től

D_{1,0}

irányába felmérjük

B_{1} D_{0} = s

-et. A

D_{0}

-on át

D_{1,0} D_{1}

-gyel párhuzamos egyenesre

B_{1}

-ből rávetítjük

D_{1}

-et, a kapott

D^{*}

-n át

D_{1} A_{1}

, és

D_{1} C_{1}

-gyel húzott párhuzamosok az

A_{1} B_{1} C_{1}

szög száraiból kimetszik

A^{*}

és

C^{*}

-ot, ekkor

A^{*} B_{1} C^{*} D^{*}

a kívánt trapéz. Ez megfelel a követelményeknek, mert szögei az előírtak, másrészt a

D^{*} A^{*} D_{0}

háromszög hasonló

D_{1} A_{1} D_{1,0}

-hoz, tehát egyenlő szárú és így

B_{1} A^{*} + A^{*} D^{*} = B_{1} A^{*} + A^{*} D_{0} = s

. A szerkesztés egyértelműen végrehajtható.
2. Legyen másodszor

B A D ∢ = 90^{\circ}

A B C ∢ = β

B A + A D = s

, és

A D = x

, ahol

0 < x < s

. Így

B A = s - x

, és a fentiekhez hasonlóan

D C = s - x - x ctg β

‐ mert a

B C

szár

D C

-n levő

C B'

vetületének hosszát (lásd a 2. ábrán

C_{1} B'

-ben) a

B C B'

derékszögű háromszögből a

B B' ctg β = x ctg β

szorzat abszolút értéke adja és

ctg β

hegyes és tompa szögekre ellentett jelű. Így a középvonal

s - x - (x ctg β) / 2 = s - (2 + ctg β) x / 2

, másrészt a magasság

x

, tehát a terület:

\begin{matrix} t = y_{2} = s x - \frac{1}{2} (2 + ctg β) x^{2} . \end{matrix}

Ennek az előbbiekhez hasonlóan legnagyobb értéke van az

\begin{matrix} x^{*} = \frac{s}{2 + ctg β} \end{matrix}

helyen, ha

2 + ctg β

pozitív, vagyis

ctg β > - 2

x^{*}

akkor esik 0 és

s

közé, ha

2 + ctg β > 1

, vagyis

ctg β > - 1

β < 135^{\circ}

. Ilyenkor itt is áll

D^{*} C^{*} = x^{*} = A^{*} D^{*}

, ennek alapján a fenti hasonlósági transzformáció ismét használható,

180^{\circ} - α

helyett

90^{\circ}

-ot és

D_{1} C_{1} B_{1} ∢ = 90^{\circ}

helyett

180^{\circ} - β

szöget használva.

β < 135^{\circ}

és

D^{*} A^{*} = D^{*} C^{*}

folytán a trapéz konvex és nem fajul el.
Ha

β = 135^{\circ}

, akkor

2 + ctg β = 1

, és

x^{*} = A^{*} D^{*} = s

B A^{*} = 0

, vagyis a legnagyobb területű trapéz elfajul. (Az

x = s

értéket éppen az elfajult esetek kiküszöbölése végett zártuk ki.) Ugyanez adódik a

β > 135^{\circ}

esetekre a következő meggondolásokból.
Ha

0 < 2 + ctg β < 1

, vagyis

135^{\circ} < β < 153, 4^{\circ}

, akkor

y_{2}

képe olyan parabola, melynek csúcsa ,,fönt'' van,

y_{2}

x^{*} > s

helyen veszi fel legnagyobb értékét, az

x < x^{*}

értékekre növekvő. Ide esnek a minket érdeklő

0 < x < s

értékek, közülük ismét az

x = s

-nél volna legnagyobb

y_{2}

értéke.

2 + ctg β = 0

β \approx 153, 4^{\circ}

esetén

y_{2}

növekvő elsőfokú függvény.

2 + ctg β < 0

esetén

y_{2}

-ben

x^{2}

együtthatója pozitív,

y_{2}

képének ,,lent'' van a csúcsa, de ennek

x^{*}

abszcisszája negatív, így a minket érdeklő

0 < x < s

értékekre

y_{2}

ismét növekvő, legnagyobb volna a meg nem engedett

x = s

-nél.
Ezzel vizsgálatunkat befejeztük.

Összeállítva Hajna János (Pécs, Széchenyi I. g. IV. o. t.)

és Máté Zsolt (Szeged, Radnóti M. g. IV. o. t.)

dolgozataiból, kiegészítésekkel és rövidítésekkel.

Megjegyzések. A beérkezett dolgozatok szerzőinek javarésze sok munkát fektetett megoldásába, ezért az átlagosnál több probléma, téves nézet merült fel. Alább néhányat szóvá teszünk.
1. Sok oda nem való elem tapad a trapéz fogalmához. 1. ábránkon éppen avégett forgattuk el a trapézt a ,,hagyományos'' helyzetből, hogy olvasóinkat a geometriai tényeknek bármely helyzetben való felismerésére szoktassuk. Háromszögeknél nem ütközünk meg azon, hogy nem minden magasság ,,függőleges'', így a trapézok alapjairól se higgyük, hogy okvetlen ,,vízszintesek'', ‐ amint nem egy dolgozat írta. Még többen voltak, akik lényeges különbséget tettek az alsó és a felső (a nagyobb és a kisebb) alap között, és a kérdést 4 esetben vizsgálták aszerint, amint az

a + b

a + d

c + b

c + d

összeg állandó (

a

és

c

a párhuzamos oldalak,

a > c

, és

b

a merőleges szár). Ez egyfelől helyes körültekintés, teljességre való törekvés, másfelől van benne lényeg nem látás is. Nem egy ilyen dolgozat kimondta pl. az

a + b = s

és

c + b = s

esetek hasonlóságát (pl. így: ,,semmi újat nem mond''), de nem jutott el a két eset összevonásáig.
2. Jónéhány dolgozat szükségtelenül a differenciálszámításnak a függvények szélső értékei megállapítására vonatkozó módszereiből alkalmazta a legismertebbet, hogy ti. bizonyos egyszerű függvényeknek csak ott lehet helyi szélső értékük, ahol differenciálhányadosuk értéke 0. Azt azonban már többnyire nem vizsgálták e dolgozatok, hogy valóban van-e a kérdéses helyen szélső érték, és ha van, akkor milyen természetű, és hogy a kérdéses hely beleesik-e a változó számára figyelembe veendő intervallumba. Megfelelő diszkusszió nélkül e tanulók ugyanúgy hibás eredményekre jutottak vagy juthattak volna, amint a differenciálszámítás kialakulásának kezdetén egyes kutatók téves megállapításokra jutottak.
3. Szórványosan előfordult a szövegnek az a téves értelmezése, hogy minden két szomszédos oldal összege állandó. Így nem volna változási lehetőség.
4. Több jó dolgozat annyira csupán számítási kérdésnek tekintette a feladatot, hogy a szerkesztésről csak efféle megjegyzést tett: ,,az eredmények megszerkeszthetők''; ezek kissé hiányosak.