Kezdőlap


Feladat:	1007. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bollobás Béla , Gagyi Pálffy András , Gálfi László , Góth László , Máté Zsolt
Füzet:	1960/november, 110 - 112. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Körülírt kör középpontja, Indirekt bizonyítási mód, Térgeometriai bizonyítások, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1959/november: 1007. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Sem a háromszög $a$ , $b$ , $c$ oldalegyenesein, sem a kérdéses $e$ egyenesen nincs szó irányításról. Így két egyenes szögén mindig azt a kisebb forgást érthetjük, amely egyiküket a közös pontja körül a másikba, ill. kitérő egyenesek esetében egy tetszés szerinti pontja körül a másikkal párhuzamos helyzetbe átviszi. Ez a forgás általában hegyes szög, legfeljebb derékszög.

I. megoldás: Az

e

egyenes nem fekhet a háromszög

S

síkjában és azzal párhuzamos sem lehet. Ha ugyanis

e

S

-ben feküdnék, akkor

a

és

b

-vel alkotott egyenlő

α

szögei alapján vagy azonos, vagy párhuzamos lenne az

a

és

b

egyenesek szögfelezőinek egyikével,

f

-fel (1. ábra,

α

hegyes szög, mert fele az

a

b

oldalegyenesek valamelyik szögének).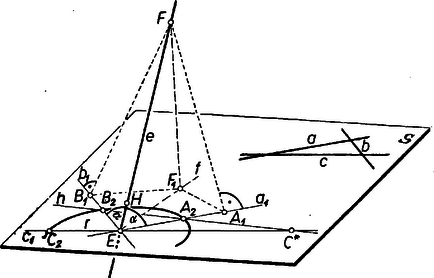

1. ábra

Így

c

α

szöget alkotna

f

-fel. Ámde egy egyenessel a síkban csak két irány alkot egy adott hegyesszöget, esetünkben

f

-fel

a

és

b

irányai. Eszerint

c

párhuzamos lenne

a

és

b

egyikével, tehát nem alkotna velük háromszöget. ‐ Ha pedig

e

párhuzamos volna az

S

síkkal, akkor

S

-nek bármely az

e

-vel párhuzamos

e_{1}

egyenese is egyenlő szöget alkotna

a

b

c

-vel, amiről már láttuk, hogy lehetetlen.
Ezek szerint

e

metszi

S

-et egy

E

pontban. Toljuk el

a

b

c

-t (

S

-ben) úgy, hogy új

a_{1}

b_{1}

c_{1}

helyzetükben menjenek át

E

-n (2. ábr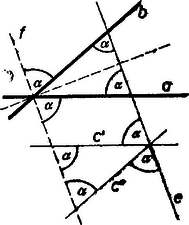a).

2. ábra

Így

e

a_{1}

b_{1}

c_{1}

-gyel is

α

szöget alkot. ‐

c_{1}

-et átmenetileg mellőzve megmutatjuk, hogy

e

benne van azon két síknak egyikében, amelyek merőlegesek

S

-re és azt

a_{1}

, és

b_{1}

egy-egy szögfelezőjében metszik. Bocsássunk merőlegest

e

-nek egy

E

-től különböző

F

pontjából

a_{1}

-re,

b_{1}

-re és

S

-re, legyenek talppontjaik

A_{1}

B_{1}

F_{1}

. Ha e három talppont és

E

közül bármelyik kettő egybeesik, akkor

e

merőleges

S

-re és segédtételünkre nincs szükség. Amennyiben ugyanis

F_{1}

azonos

E

-vel, akkor

e

azonos az

S

-re merőleges

F F_{1}

-gyel; az

A_{1} \equiv E

(és hasonlóan a

B_{1} \equiv E

) feltevés azt jelenti, hogy

e

azonos az

a_{1}

-re merőleges

F A_{1}

-gyel, így

α

derékszög, tehát a feltevésnél fogva

e

merőleges

S

-nek

a_{1}

és

b_{1}

(egymástól különböző) egyeneseire; erre vezet az

A_{1} \equiv B_{1}

feltevés is, mert így

A_{1}

és

B_{1}

azonos

a_{1}

és

b_{1}

egyetlen közös pontjával

E

-vel; végül az

F_{1} \equiv A_{1}

, (vagy

F_{1} \equiv B_{1}

) egybeesés feltevése ‐ ha feltesszük, hogy

A_{1}

B_{1}

és

E

különbözők ‐ ellentmondásra vezet, ugyanis így

S

-nek

F

-től való távolsága

F A_{1}

, és

S

-nek minden az

A_{1}

-től különböző pontja

F

-től nagyobb távolságra van

F A_{1}

-nél, viszont a közös átfogójú

F E A_{1}

, és

F E B_{1}

, derékszögű háromszögek egybevágók, mert

E

-nél levő szögeik egyenlők, és ezért

F B_{1} = F A_{1}

. ‐ Ha az

A_{1}

B_{1}

F_{1}

talppontok különbözők, akkor

F_{1}

rajta van

a_{1}

és

b_{1}

egyik szögfelezőjén. Ugyanis az

F E A_{1}

és

F E B_{1}

háromszögekből ismét

F B_{1} = F A_{1}

, így a közös befogójú

F F_{1} A_{1}

és

F F_{1} B_{1}

derékszögű háromszögek egybevágók, így

F_{1} A_{1} = F_{1} B_{1}

, ez pedig igazolja állításunkat, mert szerkesztésnél fogva

F_{1} A_{1}

merőleges

a_{1}

-re és

F_{1} B_{1}

merőleges

b_{1}

-re. Ezek szerint

e

-nek

S

-en való vetülete az

E F_{1} = f

szögfelező, és fordítva:

e

valóban az

f

-en át

S

-re merőlegesen álló

S_{1}

síkban van.
Eredményünk szerint

e

a_{1}

c_{1}

, egyenespár egyik

g

szögfelezőjén át

S

-re merőlegesen álló

S_{2}

síkban is benne van. Ámde az

a_{1}

c_{1}

, egyenespár mindkét szögfelezője különbözik az

a_{1}

b_{1}

pár mindkét szögfelezőjétől, mert e felezők párhuzamosak az eredeti háromszög egy-egy belső, ill. külső szögfelezőjével, azok pedig páronként metszik egymást. Ezért

S_{1}

és

S_{2}

, különbözők, tehát

e

csak

S_{1}

és

S_{2}

metszésvonala lehet, ez pedig az

S

-re

E

-ben emelt merőleges. Ezt kellett bebizonyítanunk.

Gagyi Pálffy András (Budapest, Széchenyi I. g. III. o. t.)

Megjegyzés. Az

a_{1}

b_{1}

, metsző egyenesekhez képezett

S_{1}

síkot

a_{1}

és

b_{1}

(egyik) szögfelező síkjának szokás nevezni. Könnyű belátni, hogy ennek minden pontja egyenlő távolságra van

a_{1}

és

b_{1}

-től.

II. megoldás: Az I. megoldás jelölésével vegyünk

e

-n egy

E

-től különböző

F

pontot és mérjünk fel

E

-től

a_{1}

b_{1}

c_{1}

-re tetszés szerinti

E A_{2} = E B_{2} = E C_{2} = r

szakaszt, az irányokat úgy választva, hogy a

F E A_{2}

F E B_{2}

F E C_{2}

háromszögek

E

-nél levő szöge egyenlő legyen. Így e háromszögek egybevágók (két-két oldal és a közbezárt szög egyenlősége folytán), tehát

F A_{2} = F B_{2} = F C_{2}

. Ennélfogva

A_{2} B_{2} C_{2}

egy az

F

körül írt gömbön vannak, másrészt

S

-en, tehát

F

és

S

metszésvonalán, amely egy kör, és középpontja

F

-nek

S

-en levő

F_{1}

vetülete. Ámde másrészt

A

B

C

E

körül

r

sugárral írt körön is rajta vannak. És mivel 3 pont a kört egyértelműen meghatározza, azért

F_{1}

azonos

E

-vel, tehát

e

merőleges

S

-re.

Máté Zsolt (Szeged, Radnóti M. g. IV. o. t.)

III. megoldás: Az előbbi jelöléseket használva tegyük fel, hogy

e

nem merőleges

S

-re, tehát

a_{1}

b_{1}

c_{1}

-gyel egyenlő hegyesszögeket alkot. Állítsunk

e

-re egy az

E

-től különböző

H

pontján át merőleges

S^{*}

síkot. Ez metszi

S

-et egy

h

egyenesben (amely eszerint merőleges

e

-re),

h

pedig

a_{1}

b_{1}

c_{1}

közül legalább kettőt metsz, mert ezek között nincsenek párhuzamosak. Nem lehet azonban, hogy

h

pl.

a_{1}

-et ne messe, mert akkor

h

és

a_{1}

párhuzamosak volnának, és

e

h

-val együtt az

a_{1}

-re is merőleges lenne, feltevésünkkel ellentétben.
Legyen

h

metszéspontja

a_{1}

b_{1}

c_{1}

-en

A^{*}

B^{*}

C^{*}

. ¹ A

H E A^{*}

H E B^{*}

H E C^{*}

derékszögű háromszögek

H E

befogója közös,

E

-nél levő szögeik egyenlők, így egybevágók, tehát

E A^{*} = E B^{*} = E C^{*}

, vagyis

A^{*}

B^{*}

C^{*}

egy az

E

körüli

k

körön vannak. Ez azonban lehetetlen, mert így

k

-nak a

h

egyenessel három különböző közös pontja lenne. Feltevésünk ellentmondásra vezetett, tehát nem állhat, így

e

merőleges

S

-re.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

Megjegyzés. Végső soron a következő meggondolás is arra vezet, hogy ha

e

nem volna merőleges

S

-re, vagyis

a_{1}

b_{1}

c_{1}

-re, hanem velük bezárt

α

szöge hegyesszög volna, akkor egy körnek és egy egyenesnek három közös pontja volna. Az

e

-t

E

-ben metsző és vele egyenlő

α

szögeket alkotó egyenesek mértani helye (ha az

α = 90^{\circ}

esetet kizárjuk), az

E

csúcsú,

e

tengelyű és

α

nyílásszögű forgáskúpfelület alkotóinak összessége. Ha

α

hegyesszög, akkor az említett kúpfelületnek (legalább) három alkotója volna

S

-ben:

a_{1}

b_{1}

c_{1}

. Ez pedig lehetetlen, mert így a fenti

S^{*}

által az

S

-ből kimetszett

h

-nak három közös pontja volna az

S^{*}

által a kúpfelületből kimetszett

k'

körrel.

Góth László (Budapest, Könyves Kálmán g. II. o. t.)

IV. megoldás: Az állítást a vektoralgebra módszereivel is bebizonyíthatjuk. ² Legyenek a háromszög oldalainak vektorai (valamelyik körüljárás mentén haladva)

a

b

c

, eszerint

\begin{matrix} a + b + c = 0 \end{matrix}

(1)

továbbá az oldalakkal egyenlő

α

szögeket bezáró egyenes egységvektora

e

, eszerint

| e | = 1

. Így

\begin{matrix} cos α = \frac{a \cdot e}{| a | \cdot | e |} = \frac{a \cdot e}{| a |} = \frac{b \cdot e}{| b |} = \frac{c \cdot e}{| c |} . \end{matrix}

(2)

Szorozzuk meg (1)-et skalárisan

e

-vel és fejezzük ki a tagokat (2) alapján:

\begin{matrix} a \cdot e + b \cdot e + c \cdot e = | a | cos α + | b | cos α + | c | cos α = & (3) \\ = (| a | + | b | + | c |) cos α = 0. \end{matrix}

Itt az abszolút értékek pozitívok, ezért az egyenlőség csak

cos α = 0

-val vagyis

α = 90^{\circ}

-kal teljesülhet. Ezt akartuk bizonyítani.

Gálfi László (Budapest, Fazekas M. gyak. g. II. o. t.)

¹Az ábrán

H

úgy van véve, hogy

A^{*} \equiv A_{2}

, és

B^{*} \equiv B_{2}

²A felhasznált fogalmakat lásd pl. Hajós‐Neukomm‐Surányi: Matematikai Versenytételek II. (Középiskola Szakköri Füzetek), Tankönyvkiadó, 1957. 26‐30. oldal.