Kezdőlap


Feladat:	1006. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Páska Csaba , Szalay Gábor
Füzet:	1960/szeptember, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Paralelepipedon, Térgeometriai bizonyítások, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1959/november: 1006. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Előkészítésül bebizonyítjuk, hogy a paralelogramma átlóinak négyzetösszege egyenlő az oldalak négyzetösszegével. Ez derékszögű paralelogrammára a Püthagorász-tétel alapján nyilvánvaló. Legyen az $A B C D$ ferdeszögű paralelogramma betűzése olyan, hogy a hegyesszögek csúcsai $A$ és $C$ , és az $A B$ oldal nem kisebb $A D$ -nél, legyen továbbá $C, D$ (derékszögű) vetülete az $A B$ oldalegyenesen $C', D'$ (1. áb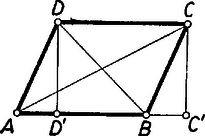ra).

1. ábra

Ekkor

D'

A B

szakaszon van,

C'

pedig e szakasz

B

-n túli meghosszabbításán, ezért

A C' = A B + B C'

és

D' B = A B - A D'

, továbbá

B C' = A D'

és

A B = D C

. Így az átlók négyzetei az

A C' C

és

B D' D

derékszögű háromszögekből:

\begin{matrix} A C^{2} & = A C'^{2} + C' C^{2} = A B^{2} + 2 A B \cdot B C' + (B C'^{2} + C' C^{2}) = \\ = A B^{2} + 2 A B \cdot A D' + B C^{2}, \\ B D^{2} & = D' B^{2} + D' D^{2} = A B^{2} - 2 A B \cdot A D' + (A D'^{2} + D' D^{2}) = \\ = D C^{2} - 2 A B \cdot A D' + A D^{2}, \end{matrix}

tehát összegükre fennáll

\begin{matrix} A C^{2} + B D^{2} = A B^{2} + D C^{2} + A D^{2} + B C^{2}, \end{matrix}

(1)

amit bizonyítani akartunk.

Legyen az

A B C D

paralelogrammát alaplapként tartalmazó

A B C D E F G H = P

paralelepipedon betűzése olyan, hogy az oldalélek

A E

B F

C G

és

D H

, tehát ezek párhuzamosak és egyenlők (2. ábra).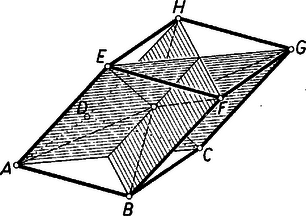

2. ábra

Így

P

testátlói az

A G

B H

C E

és

D F

szakaszok. Alkalmazzuk a fenti segédtételt

P

-nek

A C G E

és

B F H D

átlós síkmetszeteire, amelyek paralelogrammák, és átlóik az

A G

és

C E

, ill.

B H

és

D F

testátlópárok, majd adjuk össze az egyenlőségeket:

\begin{matrix} A G^{2} + C E^{2} = A C^{2} + E G^{2} + A E^{2} + C G^{2}, \\ B H^{2} + D F^{2} = B D^{2} + F H^{2} + B F^{2} + D H^{2}, \\ S = A G^{2} + B H^{2} + C E^{2} + D F^{2} = (A C^{2} + B D^{2}) + (E G^{2} + F H^{2}) + \\ + (A E^{2} + B F^{2} + C G^{2} + D H^{2}) . \end{matrix}

Itt ugyancsak a segédtétel alapján az első zárójel helyett (1) jobb oldalát, a második zárójel helyett pedig az

E F G H

paralelogramma oldalainak négyzetösszegét írva az állítást igazoltuk, ugyanis

\begin{matrix} S = (A B^{2} + D C^{2} + A D^{2} + B C^{2}) + (E F^{2} + H G^{2} + E H^{2} + F G^{2}) + \\ + (A E^{2} + B F^{2} + C G^{2} + D H^{2}) = \\ = (A B^{2} + D C^{2} + H G^{2} + E F^{2}) + (A D^{2} + B C^{2} + F G^{2} + E H^{2}) + \\ + (A E^{2} + B F^{2} + C G^{2} + D H^{2}), \end{matrix}

és ezt kellett bizonyítanunk.

Szalay Gábor (Budapest, I. László g. III. o. t.)

II. megoldás: Az állítás vektoralgebrai úton is igazolható. ^{$^{*}$} Legyen az

A

csúcsból a szomszédos

B

D

E

csúcsba mutató élvektor

a

b

és

c

, ekkor az átlók vektorai

\begin{matrix} \vec{A G} = a + b + c, \vec{B H} = -a + b + c, \vec{C E} = - a - b + c, \vec{D F} = a - b + c, \end{matrix}

és így négyzetösszegük:

\begin{matrix} S & = (A G^{2} + B H^{2}) + (C E^{2} + D F^{2}) = [{(b + c + a)}^{2} + {(b + c - a)}^{2}] + \\ + [{(c - b - a)}^{2} + {(c - b + a)}^{2}] = [2 {(b + c)}^{2} + 2 a^{2}] + [2 {(c - b)}^{2} + \\ + 2 a^{2}] = 4 a^{2} + 2 [{(b + c)}^{2} + {(b - c)}^{2}] = 4 a^{2} + 2 [2 b^{2} + 2 c^{2}] = 4 (a^{2} + b^{2} + c^{2}) . \end{matrix}

Páska Csaba (Budapest, I. István g. III. o. t.)

^{$^{*}$}A felhasznált fogalmakat lásd pl. Hajós‐Neukomm‐Surányi: Matematikai Versenytételek II. (Középiskolai Szakköri Füzetek) Tankönyvkiadó, 1957. 26‐30. o.