Kezdőlap


Feladat:	1004. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Krámli András , Náray-Szabó Gábor , Szoboszlai Levente
Füzet:	1960/október, 58 - 60. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1959/november: 1004. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feltevésnél fogva egyik szög koszinusza sem 0, így a bizonyítandó

\begin{matrix} sin α sin β sin γ > 5 cos α cos β cos γ \end{matrix}

egyenlőtlenség mindkét oldalát oszthatjuk a koszinuszok szorzatával, ezért elegendő azt megmutatni, hogy

\begin{matrix} tg α tg β tg γ > 5. \end{matrix}

(1)

Ismeretes, hogy a bármely nem derékszögű háromszög szögeinek tangenséből képezett összeg és szorzat egyenlők:

\begin{matrix} tg α + tg β + tg γ = tg α tg β tg γ . \end{matrix}

(2)

Belátható ez a tangens-függvény összeadási tételéből, az

α + β + γ = 180^{\circ}

összefüggésre támaszkodva, ha vesszük a

\begin{matrix} tg γ = tg [180^{\circ} - (α + β)] = - tg (α + β) = \frac{- tg α + tg β}{1 - tg α tg β} \end{matrix}

egyenlőség-sorozat szélső kifejezéseinek egyenlőségét, és azt átrendezzük.) Feltevésünknél fogva mindhárom tangens pozitív, így számtani közepük nem kisebb a mértani közepüknél:

\begin{matrix} \frac{tg α + tg β + tg γ}{3} \geq \sqrt[3]{tg α tg β tg γ} . \end{matrix}

Innen az összeget (2) alapján a szorzattal helyettesítve, majd köbreemeléssel és osztással, végül a jobb oldal csökkentésével

\begin{matrix} {tg}^{2} α {tg}^{2} β {tg}^{2} γ \geq 27 > 25 \end{matrix}

adódik, ebből pedig négyzetgyökvonással (1)-re jutunk.
(Felhasználtuk, hogy két pozitív szám közül a nagyobbnak a köbe nagyobb.)

Szoboszlai Levente (Hódmezővásárhely, Bethlen G. g. III. o. t.)

Megjegyzés. A feladat állítása minden háromszögre érvényes. Ugyanis derékszögű háromszögekre a koszinuszok szorzata 0, tompaszögűekre pedig negatív ‐ mert a tompaszög koszinusza negatív ‐, viszont a háromszög bármelyik szögének szinusza pozitív, és így ugyanez áll szorzatukra is.

Náray Szabó Gábor (Budapest, József A. g. III. o. t.)

II. megoldás: Ismert tétel, hogy egy adott kör köré írt háromszögek közül a szabályos háromszögnek van a legkisebb kerülete. Ennek felhasználásával az állítás így is bizonyítható:
Legyenek egy tetszés szerinti hegyesszögű háromszög szögei

α

β

γ

. Mérjük fel egy

ϱ

sugarú

k

kör

O T_{1}

sugarától kezdve egymás után az

α

α

β

β

γ

γ

nagyságú szögeket úgy, hogy valamennyi szög csúcsa az

O

középpont legyen.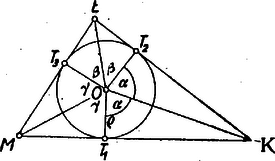

1. ábra

Ekkor a második

γ

szög második szára

O T_{1}

-be esik. Messe

k

-t a szomszédos

α

és

β

szögek közös szára

T_{2}

-ben, a szomszédos

β

és

γ

szögek közös szára

T_{3}

-ban. Húzzuk meg

k

érintőit

T_{1}

T_{2}

T_{3}

-ban. Nyilvánvaló, hogy e három érintő a szomszédos

α

α

, ill.

β

β

ill.

γ

γ

nagyságú szögek közös szárát páronkint ugyanazon

K

, ill.

L

, ill.

M

pontban metszi (1. ábra), és hogy a

K L M

háromszög

k

köré van írva, ezért

K T_{1} = K T_{2}

L T_{2} = L T_{3}

M T_{3} = M T_{1}

. A létrejött derékszögű háromszögekből

\begin{matrix} tg α + tg β + tg γ = \frac{K T_{1}}{ϱ} + \frac{L T_{2}}{ϱ} + \frac{M T_{3}}{ϱ} = \frac{s}{ϱ}, \end{matrix}

(3)

ahol

s

K L M

háromszög kerületének felét jelöli. Másrészt az idézett tétel szerint (

a

-val jelölve a

k

köré írható szabályos háromszög oldalát):

\begin{matrix} \frac{s}{ϱ} \geq \frac{3 a}{2} : \frac{a \sqrt[]{3}}{6} = 3 \sqrt[]{3} = \sqrt[]{27} > 5, \end{matrix}

amiből (2) és (3) figyelembevételével (1) adódik.

Krámli András (Szeged, Radnóti M. g. III. o. t.)

Megjegyzés. A felhasznált tétel akárhány oldalú sokszögre érvényes,^{$^{*}$} háromszögre az alábbiak szerint látható be.

t = ϱ s

folytán elég megmutatni, hogy adott

k

kör köré irt háromszögek közül a szabályos területe a legkisebb. Legyen egy

k

köré irt szabályos háromszög oldala

a

, körülírt köre (amely korcentrkus

k

-val)

k'

(2. áb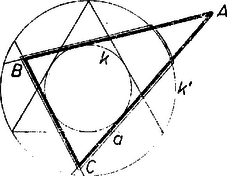ra).

2. ábra

Egy a

k

köré írt, tetszés szerinti, nem szabályos

A B C

háromszög oldalegyeneseinek ugyancsak

a

hosszúságú húrjai esnek

k'

-be, így abból ugyanakkora körszeleteket és köríveket metszenek le, mint a szabályos háromszög oldalai, a körívek hossza egyenlő a kör kerületének harmadrészével. A lemetszett ívek részben fedik egymást, különben

A B C

szabályos háromszög volna. Ezért a lemetszett körszeletek is részben fedik egymást, így pedig az

A B C

háromszögnek már a

k'

-be eső része nagyobb területű, mint az

a

oldalú szabályos háromszög (éspedig annyival nagyobb, amennyi a három körszelet által kétszer lefedett terület).

^{$^{*}$}Lásd Fejes Tóth László: Körbe és kör köré írt sokszögekről. Matematikai Lapok, X. évf. (1959), 23‐25. l.