Feladat: 996. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bodosi Tamás ,  Frint Gábor ,  Kardeván Péter ,  Noszticzius Zoltán ,  Pál Gábor 
Füzet: 1960/április, 122 - 125. oldal  PDF  |  MathML 
Témakör(ök): Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1959/október: 996. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. A dolgozatok között az olyanok vannak nagyobb számban, amelyek az állítást trigonometriai számítás útján bizonyítják. Egy ilyen rövid és egyszerű bizonyítás a következő.

 

I. megoldás: Ismert azonosságok alapján a feltevés átalakításával
a+cb=ab+cb=sinα+sinγsinβ=2sinα+γ2cosγ-α2sinβ=2cosγ-α2=2,
innen (γ-α)/2=45∘ és γ-α=90∘, amit bizonyítanunk kellett.
 

Pál Gábor (Miskolc, Gábor Á. kohó- és öntőip. t. IV. o. t.)

Sokkal kevesebb előismeret elegendő a megoldáshoz. A továbbiakban ilyen megoldásokat mutatunk be.
 

II. megoldás: β számtani közepe α és γ-nak, eszerint α,β,γ számtani sorozatot alkotnak. Ilyen számhármas középső tagja az összegüknek harmadrésze, ezért β=60∘. Másrészt a c>a feltevés folytán γ>α, és így α<60∘<γ.
Forgassuk rá a BC oldalt AB-nek B-n túli meghosszabbítására: BD=BC=a, és így AD=a+c, másrészt a BCD egyenlő szárú háromszögből BCD∢=BDC∢=β/2=30∘. Legyen A vetülete a CD egyenesen E.
 
 
2. ábra
 

Így az ADE szög 30∘ és az ADE derékszögű háromszög úgy tekinthető, mintha egy AD=a+c oldalú szabályos háromszögből jött volna létre egy magassággal való kettévágás útján, ezért AE=AD/2=(a+c)/2. Ez a feltevés folytán egyenlő b/2-vel, a b átfogó fölé írt egyenlő szárú derékszögű háromszög befogójával. Így az ACE derékszögű háromszög egyenlő szárú, mert hasonló bármely egyenlő szárú derékszögű háromszöghöz, hiszen megegyeznek két oldal arányában (AC:AE=2) és az ezek nagyobbikával szemben fekvő derékszögben. Eszerint ACE∢=45∘, ACD∢=135∘, ezekből γ=ACB∢=ACD∢-BCD∢=135∘-30∘=105∘, másrészt α=15∘, és így valóban γ=α+90∘.
 

Bodosi Tamás (Kaposvár, Táncsics M. g. IV. o. t.)

A továbbiakban β=60∘-ot ismertnek vesszük, másrészt az α=15∘ érték megállapítása után a megoldást befejezettnek tekintjük.
 

III. megoldás: Az adatoknak megfelelő alakú háromszöghöz jutunk a következő úton. A β=60∘ és b2=a+c összefüggések azt a gondolatot adják, rajzoljuk meg a DE=b szakasz egyik oldalára illeszkedő 60∘-os látószögkörívet és az E-nél derékszögű DEF egyenlő szárú háromszöget, ebben ugyanis DF=b2. Messe a körív a 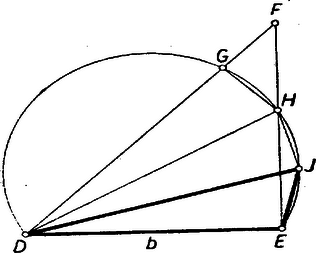DF,EF oldalt G, ill. H-ban.
 
 
1. ábra
 

Ekkor DH az ívnek átmérője (az ív ugyanis nyilvánvalóan nagyobb félkörnél) így DGH∢=FGH∢=90∘, másrészt DFE∢=GFH∢=45∘, ezért az FGH háromszög egyenlő szárú: GF=GH. Továbbá DHE∢=60∘, ezért HDE∢=30∘, másrészt GDE∢=45∘, és így GDH∢=15∘. Ha most a H körül GH sugárral írt kör az ívet másodszor J-ben metszi, akkor a mondott háromszög alak DJE. Ebben ugyanis HJ=HG folytán egyrészt HDJ∢=HDG∢=15∘, ezért JDE∢=HDE∢-HDJ∢=30∘-15∘=15∘=HDJ∢, és így JE=JH=HG=GF; másrészt a JDH és GDH derékszögű háromszögek egybevágók, ezért JD=GD. Ezek szerint a DJE háromszög J-ből kiinduló oldalaira JD+JE=GD+GF=DF=DE2 és J-nél fekvő szöge 60∘, vagyis a DJE háromszögben feladatunk mindkét egyenlőségi feltevése teljesül.
E két feltevés a háromszög alakját (azaz szögeit, más szóval a háromszöget hasonlóság erejéig) egyértelműen meghatározza (ugyanis az oldalak közti összefüggés az a/b+c/b=2 alakban az oldalak arányai közötti összefüggést ad). Ennélfogva minden, a feltevésnek megfelelő háromszögben a további szögek EDJ∢=15∘-kal, ill. DEJ∢=180∘-(60∘+15∘)=105∘-kal egyenlők.
 

Frint Gábor (Mosonmagyaróvár, Kossuth L. g. III. o. t.)
 

IV. megoldás: A bizonyítandó állítást γ-90∘=α alakban írva elég azt megmutatnunk, hogy a BC oldalra C-ben állított merőleges az AB oldalt olyan belső D pontban metszi, amellyel az ACD háromszög ACD=γ-90∘ és CAD=α szögei egyenlők. Ehhez pedig elegendő AD=DC fennállását belátni.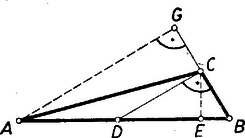
 
 


Ha C vetülete AB-n E, akkor a BCE háromszögből CE=a3/2, BE=a/2, és mivel β<90∘ folytán E az AB-n van, AE=c-a/2. Így az ACE derékszögű háromszögből Püthagorász tétele, valamint a feltevés alapján összefüggést kapunk a és c között:
b2=(a+c2)2=(c-a2)2+(a32)2,
ebből
a2-4ac+c2=0,
és c=2a+a3 (a kisebb gyök nem felel meg a c>a követelménynek): Másrészt a BCD derékszögű háromszögből CD=a3 és BD=2BC=2a.
Most már látható, hogy D valóban az AB-n fekszik, ugyanis BA>BD, mert c>2a, továbbá, hogy AD=AB-BD=c-2a=a3=CD, amit bizonyítani akartunk.
 

Kardeván Péter (Mosonmagyaróvár, Kossuth L. g. III. o. t.)
 

Megjegyzés. A c=2a+a3 eredmény felhasználásával az a=15∘ eredményt így is igazolhatjuk. Ha A-nak BC-n levő vetülete G, akkor AC felezi a BAG=30∘-os szöget, mert a BG oldal C-vel való kettéosztásakor keletkezett részek GC:BC aránya megegyezik GA és BA arányával. Az utóbbi, mint már láttuk, 3/2-vel egyenlő, másrészt BG=c/2 és a fenti c=2a+a3 alapján a másik arány értéke ugyanennyi:

GC=BG-BC=c/2-a=(c-2a)/2=a3/2=BC3/2.
 

Noszticzius Zoltán (Budapest, József A. g. IV. o. t.)