Kezdőlap


Feladat:	995. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bollobás B. , Frint G. , Fritz J. , Grüner Gy. , Hajna J. , Molnár E. , Nagy Dezső , Tomcsányi Gy. , Tomcsányi Gyula , Várady G. , Veres Gy.
Füzet:	1960/április, 121 - 122. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Kocka, Téglatest, Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1959/október: 995. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a papírlemez oldala $a$ , a hasáb alapéle $b$ , magassága $m$ . A hálózat egy $b$ oldalú négyzetből és négy $b$ és $m$ oldalakkal bíró téglalapból áll. Egy darabban leendő elkészítéséhez a lapokat $8$ -féleképpen rendezhetjük el. Tekintsük közülük a legegyszerűbb, legtetszetősebb típust, azt, amelyben mind a négy alapél hajtással és mind a négy oldalél ragasztással alakul ki (ennek ugyanis négyes forgási szimmetriája és négy szimmetriatengelye van), ezzel várható, hogy $b$ és $m$ legnagyobbra vehető. Ilyen hálózat úgy szerkeszthető, ha a négyzetlemezbe két olyan téglalapot írunk az átlókkal párhuzamos oldalakkal, melynek oldalai $b$ és $b + 2 m$ , közös részük a $b$ oldalú négyzet.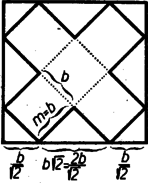

1. ábra

Kockát az

m = b

esetben kapunk (1. ábra); ekkor a berajzolt téglalapok oldalai

b

és

3 b

. A lemez egy oldalára való vetületeik összege egyenlő a lemez oldalával, tehát

4 b / \sqrt[]{2} = a

és így

b = a / 2 \sqrt[]{2}

. Ezért a hálózat szabadonálló csúcsai a lemez oldalainak első és harmadik negyedrészében vannak; a térfogat: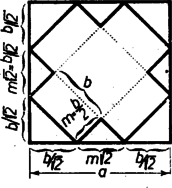

V_{k} = b^{3} = a^{3} \sqrt[]{2} / 32 = a^{3} / 16 \sqrt[]{2}

2. ábra

Általában

b / \sqrt[]{2} + (2 m + b) / \sqrt[]{2} = a

(2. ábra), és innen

b + m = a / \sqrt[]{2}

állandó, vagyis

b

növekedésével

m

csökken és viszont. A térfogat

V = b^{2} m

, amit olyan szorzattá alakíthatunk, amelyben a tényezők összege állandó:

\begin{matrix} V = b^{2} m = b \cdot b \cdot m = 4 \frac{b}{2} \cdot \frac{b}{2} \cdot m, \end{matrix}

és

V / 4

tényezőire

\begin{matrix} \frac{b}{2} + \frac{b}{2} + m = b + m = \frac{a}{\sqrt[]{2}} . \end{matrix}

Így a pozitív számok számtani és mértani közepe közti ismert egyenlőtlenséget három szám esetén alkalmazva

V / 4

értéke akkora legnagyobb, ha tényezői egyenlők:

b / 2 = m

, és így

b + m = 3 m = a / \sqrt[]{2}

m = a / 3 \sqrt[]{2}

b = a \sqrt[]{2} / 3

és

V_{max} = a^{3} \sqrt[]{2} / 27 (> V_{k}

. Az előálló test

m = b / 2

alapján nevezhető fél-kockának. A hálózat csúcsai a négyzetlemez csúcsaitól

b / \sqrt[]{2} = a / 3

távolságban vannak, a lemez oldalait 3 ‐ 3 egyenlő részre osztják.

Tomcsányi Gyula (Budapest, Toldy F. g. III. o. t)

Megjegyzések. 1. Nincs szükség a számtani és a mértani közép közti egyenlőtlenség használatára annak az előre kimondott állításnak bizonyításához, hogy legnagyobb térfogat fél-kockával adódik. Válasszuk a hálózatnak a lemez oldalain levő csúcsait a lemez csúcsaitól

a / 3

helyett

a / 3 - z

távolságban. Ekkor

b = (a / 3 - z) \sqrt[]{2}

m = a / \sqrt[]{2} - b = (a / 6 + z) \sqrt[]{2}

, a megváltozott térfogat

\begin{matrix} V (z) = b^{2} m = 2 \sqrt[]{2} {(\frac{a}{3} - z)}^{2} (\frac{a}{6} + z) = \sqrt[]{2} (\frac{a^{3}}{27} - a z^{2} + 2 z^{3}), \end{matrix}

és ennek a fél-kocka

V_{0} = a^{3} \sqrt[]{2} / 27

térfogatától való eltérése:

\begin{matrix} V (z) - V_{0} = \sqrt[]{2} z^{2} (2 z - a) . \end{matrix}

V (z)

akkor volna nagyobb

V_{0}

-nál, ha ez a különbség pozitív volna, ami csak

z > a / 2

mellett következhetne be. Ez viszont ki van zárva, mert itt

z

, a lemez csúcsaihoz való közeledés, nem érheti el az

a / 3

értéket, s így a különbség nem lehet pozitív. ‐ Vizsgálatunk azt a lehetőséget is magában foglalja, ha a hálózat csúcsait a lemez oldalán az oldal közepe felé toljuk el, ilyenkor

z

negatív, az eltérés is negatív, tehát

V_{0}

nagyobb

V (z)

-nél, ha csak

z

nem

0

M. I.

2. Tíz dolgozat említi, vagy vázlatosan vizsgálja a hálózat lapjainak néhány vagy valamennyi más lehetséges egymás mellé helyezését. Szerzőik e többletért 1 ‐ 1 jutalompontot kaptak. A többi dolgozatok 1 kivételével a bemutatott típusú hálózatot vizsgálták.
A fentihez hasonló számításokkal meg lehet mutatni, hogy a további 7 elrendezési lehetőség mindegyike esetén

V_{0}

-nál kisebb az elérhető legnagyobb térfogat. ‐ Ismert feladat viszont, hogy a hálózat hajtási és vágási vonalait a lemez oldalaival párhuzamosnak véve az elérhető legnagyobb térfogat

2 a^{3} / 27 = V_{0} \sqrt[]{2}

, ekkor a hasáb magassága negyedrésze az alapélnek.