Feladat: 994. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Holop András ,  Klimó János 
Füzet: 1960/április, 119 - 121. oldal  PDF  |  MathML 
Témakör(ök): Algebrai átalakítások, Gyökös függvények, Feladat
Hivatkozás(ok):Feladatok: 1959/október: 994. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A három kérdés megválaszolásának előkészítéséül vizsgáljuk az

y=x+2x-1+x-2x-1(1)
kifejezésnek mint x függvényének értékét, a megjegyzésnek megfelelően minden négyzetgyökvonásban a gyök abszolút értékét véve.
A belső négyzetgyök értéke akkor valós szám, ha 2x-1≧0, x≧1/2. Ilyen x-ekre mindkét (nagy) négyzetgyök valós számot ad, mert az első alatt két nem negatív szám összege áll, a másodikban pedig a kisebbítendő és a kivonandó négyzetének különbségét vizsgálva, ha x≧1/2, akkor x2-(2x-1)2=x2-2x+1=(x-1)2≧0, és mivel az alapok pozitívok, így azokra
x≧2x-1.
Az egyenlőségi jel x=1 esetére érvényes.
Mivel a két gyökjel alatti kifejezés egymásnak ún. konjugáltja, azért kifejezésünk négyzete egyszerűbbnek ígérkezik. Valóban, összevonás után
y2=2x+2x2-(2x-1)=2x+2(x-1)2=2x+2∣x-1∣.

Már most x≦1 esetére x-1 negatív vagy 0, így ∣x-1∣=-(x-1)=1-x, ezért y2=2x+2(1-x)=2, ennélfogva y=2, állandó.
x>1 esetére pedig x-1 pozitív, így ∣x-1∣=x-1, tehát y2=2x+2(x-1)=4x-2, ennélfogva y=4x-2.
Ezek szerint az a) egyenlőség az x≧1/2, x≦1 értékekre, más szóval az (1/2,1) zárt intervallumban teljesül, másutt nem; a b) egyenlőség sehol sem teljesül, ez olyan egyenlet, amelynek nincs gyöke, mert a 4x-2 kifejezés értéke az x=1 helyen 2, és x növekedtével növekszik, tehát y≧2, ha x≦1/2; végül a c) egyenlőség egyenlet, melynek gyöke x=3/2, az egyenlőség ezen egyetlen érték mellett érvényes.
 

Klimó János (Kaposvár, közg. t. IV. o. t.)

 
 

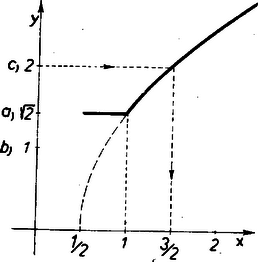II. megoldás: A bal oldalak egyszerűbbé tételére alkalmazzuk a 2x-1=z helyettesítést. A négyzetgyök értékére tett megállapodásunknak megfelelően csak z nem negatív értékeit kell figyelembe vennünk. Kifejezve x-et z-vel x=(z2+1)/2, tehát (1) a helyettesítéssel így alakul:

y=z2+12+z+z2+12-z=12(z2+1+2z+z2+1-2z)==12(z+1+∣z-1∣).


(A zárójel első tagjában az abszolút érték jelét mindjárt mellőzhettük, mert z+1≧1>0.) Innen a fentiekhez hasonlóan
0≦z≦1   esetére  y=12[z+1+(1-z)]=2,z≦1   esetére  y=12[z+1+(z-1)]=2z,  


(lásd a grafikont).
Ezek szerint az a) egyenlőség mindazon x-ekre teljesül, amelyeket a 0≦z≦1-et teljesítő z értékek adnak meg; ezekből x=(z2+1)/2-re tekintettel 0≦z2≦1, így 1≦z2+1≦2 és 1/2≦x≦1;
a b) egyenlőség semmilyen z-re és így semmilyen x-re sem teljesül, mert z≧1 mellett a bal oldal értéke: y=2z≧2>1;
a c) egyenlőség pedig 2z=2-ből z=2-vel, és ennélfogva x=(2+1)/2=3/2 mellett teljesül.
 

Holop András (Budapest, Petőfi S. g. IV. o. t.)
 

Megjegyzés. Több a II. megoldáshoz hasonló dolgozat nem zárta ki a z<0 értékeket, ezért az
y=12(∣z+1∣+∣z-1∣)
alakból tetszetősebb grafikonhoz jutott, amely a fentin kívül az Y-tengelyre való tükörképét is tartalmazza, és így rajzzal a gimnáziumi IV. osztályos tankönyvből ismert módon magyarázza y-nak a középső intervallumbeli állandóságát.