Feladat: 992. matematika feladat Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Simai László ,  Sólyom István ,  Vámos Péter 
Füzet: 1960/április, 118 - 119. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletrendszerek, Feladat
Hivatkozás(ok):Feladatok: 1959/október: 992. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Három ismeretlen meghatározására két egyenletünk van, ez általában nem elegendő. Mégis egyértelművé teszi a megoldást az a követelmény, hogy a gyökrendszerben (a középiskolai ismereteknek megfelelően) csak valós számokat fogadhatunk el.
Az első egyenletből x=y+2-t a másodikba helyettesítve, 0-ra redukálással és a teljes négyzet tagjait felismerve

y2+2y+1+z2=(y+1)2+z2=0.(1)
Két négyzet összege a valós számok körében csak úgy lehet 0, ha külön-külön is 0-val egyenlők, vagyis alapjuk is 0. Ebből y=-1, z=0, továbbá x=1. Az értékhármas az adott rendszert kielégíti.
 

Simai László (Kisújszállás, Móricz Zs. g. III. o. t.)
 

Megjegyzés. A teljes négyzet felismerése nélkül úgy is célba jutunk, ha (l)-et y-ra vonatkozó egyenletnek tekintve egyelőre csak diszkriminánsát számítjuk ki: D=-4z2. Ez csak akkor nem negatív, ha z=0.
2. A rendszert így alakítva: x+(-y)=2, x(-y)=z2+1, könnyű meglátni, hogy x és -y a t2-2t+(z2+1)=0 másodfokú egyenlet két gyökével egyenlő. Ebből is a z=0 megállapításból kiindulva adódik a fenti megoldás.
 

II. megoldás: A második egyenlet bal oldala a nem negatív z2 elhagyásával csökken, vagy változatlan marad: xy≦-1. Ezért x és y ellentett jelűek. Éspedig x pozitív, y negatív, mert x nagyobb, hiszen az első egyenlet szerint a különbségük pozitív. Legyen y abszolút értéke y1, azaz -y=y1. Ekkor
x+y1=2,xy1≧1,
vagyis a pozitív x és y1 számok számtani közepe 1, így ennek négyzete is 1, másrészt mértani közepüknek négyzete legalább 1.
Ámde a két nem negatív szám számtani és a mértani közepére (ill. négyzetükre) ismert egyenlőtlenség szerint az utóbbi nem lehet nagyobb, így xy1=1, ekkor pedig egyenlők: x=yl=-y=1, y=-1 és a második egyenletből z=0.
 

Vámos Péter (Budapest, Than K. vegyip. t. IV. o. t.)
 

Megjegyzések. 1. A II. megoldás x>0, y<0, xy≦-1, azaz y≦-1/x követelményeinek a derékszögű koordinátarendszerben az y=-1/x hiperbola negyedik negyedbeli ágán és annak ,,belsejében'' fekvő pontok tesznek eleget (vagyis az ág bármely húrjának belső pontjai), az első egyenletnek pedig az y=x-2 egyenesen fekvő pontok.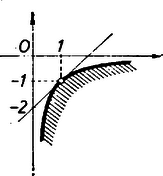
 
 

A szemlélet szerint az egyenes érinti a hiperbolát, egyetlen közös pontjuk: (1;-1).
 

Sólyom István (Budapest, Vörösmarty M. g. III. o. t.)
 

2. Az előző megjegyzésbeli észrevétel természetesen nem tekinthető a feladat megoldásának, csupán a (számításos) megoldás szemléletes megfelelőjének.