Kezdőlap


Feladat:	991. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Biborka T. , Bollobás Béla , Czékus Laborc , Dávid G. , Farkas Z. , Fejes L. , Fritz József , Gagyi Pálffy A. , Grüner György , Holop András , Kiss Ádám , Klimó J. , Kolonits Ferenc , Mezei F. , Mihályffy L. , Molnár E. , Muszély Gy. , Náray Szabó G. , Paulin F. , Tihanyi Ambrus , Tusnády Gábor , Várady Gábor
Füzet:	1960/április, 114 - 118. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Ceva-tétel, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1959/szeptember: 991. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás a feladat első részére: Nyilvánvaló, hogy a $Q_{1} Q_{2} ... Q_{6} = H_{1}$ hatszög 3 ‐ 3 oldalegyenese egymással párhuzamos, és hogy mindegyik ilyen háromtagú csoportban a leghosszabb oldal egyenlő a másik kettő összegével. Világos továbbá, hogy $H_{1}$ alakja kétféle típusú lehet: ,, $L$ alakú'' (konkáv), amelyben a két irányú leghosszabb oldalak szomszédosak, és ,,szögletes nyolcas'' alakú (hurkolt), amelyben ez a két oldal szemben fekvő (és mégis van közös pontja az oldal. szakaszoknak).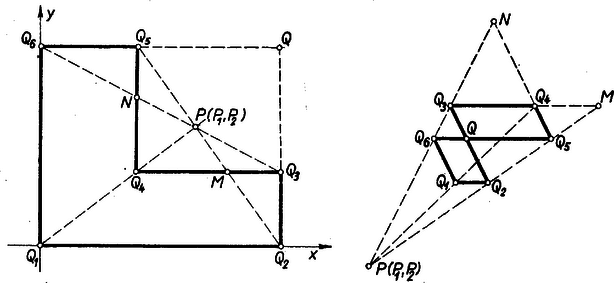

1. ábra

Messe egy konkáv

H_{1}

-nek

Q_{1} Q_{4}

átlója

Q_{2} Q_{5}

-öt

P_{1}

-ben,

Q_{3} Q_{6}

-ot

P_{2}

-ben (1. ábra), ekkor azt kell megmutatnunk, hogy

P_{2}

azonos

P_{1}

-gyel. Messe

Q_{2} Q_{5}

Q_{3} Q_{4}

oldalt

M

-ben,

Q_{3} Q_{6}

Q_{4} Q_{5}

oldalt

N

-ben, és a

Q_{2} Q_{3}

oldal a szemben fekvő

Q_{5} Q_{6}

oldalt

Q

-ban. Így az

M Q_{5} Q_{6}

és

Q_{5} Q_{2} Q

, valamint

N Q_{3} Q_{4}

és

Q_{3} Q_{6} Q

háromszögpárti hasonlóságából

\begin{matrix} Q_{4} M = \frac{Q_{4} Q_{5} \cdot Q Q_{5}}{Q Q_{2}} = \frac{Q_{4} Q_{5} \cdot Q_{3} Q_{4}}{Q_{6} Q_{1}}, Q_{4} N = \frac{Q_{3} Q_{4} \cdot Q Q_{3}}{Q Q_{6}} = \frac{Q_{3} Q_{4} \cdot Q_{4} Q_{5}}{Q_{1} Q_{2}} . \end{matrix}

Helyettesítsük ezeket az értékeket a

P_{1} Q_{4} M

és

P_{1} Q_{1} Q_{2}

, valamint

P_{2} Q_{4} N

és

P_{2} Q_{1} Q_{6}

háromszögpárok hasonlóságából adódó

\begin{matrix} P_{1} Q_{4} : P_{1} Q_{1} = Q_{4} M : Q_{1} Q_{2} és P_{2} Q_{4} : P_{2} Q_{1} = Q_{4} N : Q_{1} Q_{6} \end{matrix}

aránypárokba. Ekkor mindegyik arányra a

\begin{matrix} \frac{Q_{4} Q_{3} \cdot Q_{4} Q_{5}}{Q_{1} Q_{6} \cdot Q_{1} Q_{2}} \end{matrix}

értéket kapjuk, és ez mutatja, hogy

P_{1}

és

P_{2}

Q_{1} Q_{2}

egyenesnek ugyanaz a pontja.
Bizonyításunk betűről betűre érvényes hurkolt hatszögre is.

Kiss Ádám (Budapest, Rákóczi F. g. IV. o. t.)

Megjegyzés. A háromszögek hasonlóságában

H_{1}

-ről csak azt használtuk fel, hogy minden második oldala párhuzamos, ezért az említett átlók akkor is egy pontban metszik egymást, ha csak az említett oldalak párhuzamossága áll fenn, a szomszédos oldalak merőlegessége nem (l. a hurkolt hatszög ábráját).

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

II. megoldás az első részre: A koordinátageometria ,,gépies'' módszereivel ábrára való hivatkozás nélkül is bizonyíthatjuk az állítást, vagyis anélkül, hogy tekintettel lennénk

H_{1}

alakjának típusára. Válasszuk kezdőpontnak

Q_{1}

-et, tengelyeknek a

Q_{1} Q_{2}

Q_{1} Q_{6}

egyeneseket, legyenek továbbá

Q_{2}, Q_{3}, Q_{4}, Q_{5}, Q_{6}

koordinátái rendre

(a,0)

(a, c)

(b, c)

(b, d)

(0, d)

. Így a

Q_{2} Q_{5}

, ill.

Q_{3} Q_{6}

átló egyenlete

\begin{matrix} y = \frac{d}{b - a} (x - a), y = d + \frac{c - d}{a} x, \end{matrix}

így

P

metszéspontjuk koordinátái:

\begin{matrix} x = \frac{a b c}{a c + b d - b c}, y = \frac{a c d}{a c + b d - b c} . \end{matrix}

Innen

y / x = c / b

, ami éppen a

Q_{1} Q_{4}

átló egyenlete; ez azt mutatja, hogy

P

-n ez az átló is átmegy.

Tihanyi Ambrus (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

Megjegyzések. 1. Ez a módszer könnyűvé teszi a

P

pont létezésének diszkusszióját.

P

‐ mint

Q_{2} Q_{5}

és

Q_{3} Q_{6}

metszéspontja ‐ akkor és csak akkor nem létezik, ha e két átló párhuzamos, iránytényezőik egyenlők, vagy ami ugyanaz, ha

P

kiszámított koordinátáinak közös nevezője

0

. Az

a c + b d - b c = 0

feltevésből viszont

d = (b - a) c / d

, és ebből

Q_{2} Q_{5}

iránytényezője:

d / (b - a) = c / b

, ami egyenlő

Q_{1} Q_{4}

iránytényezőjével, ilyenkor tehát mindhárom átló párhuzamos (és ezért a feladat második részében mind hat

q_{i}

párhuzamos, az

R_{1} R_{2} ... R_{6}

hatszög nem létezik).
2. Meg lehet mutatni, hogy ez az elfajulás csak hurkolt

H_{1}

-nél következhet be.
3. Az állítást Fritz József, Holop András és Kolonits Ferenc a Ceva-tétel felhasználásával bizonyította.

I. megoldás a feladat további részére: Megmutatjuk, hogy a

P, R_{6}, R_{1}, R_{2}

pontnégyes húrnégyszöget és így egy

k

kört határoz meg (2. ábra, lásd a 990. feladat 2. ábráját is), mert

R_{6}

-nál levő belső és

R_{2}

-nél levő külső szöge egyenlő.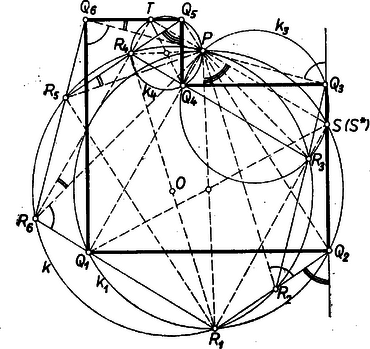

3. ábra

Ehhez felhasználjuk, hogy (1)

P Q_{6} R_{6} Q_{1}

és (2)

P Q_{2} R_{2} Q_{3}

q

-egyenesek szerkesztésénél fogva húrnégyszögek, hogy (3)

H_{1}

-nek

Q_{6} Q_{1}

és

Q_{2} Q_{3}

oldalai párhuzamosak és hogy (4)

P

Q_{3} Q_{6}

egyenes pontja. Így (1) alapján

P R_{6} R_{1} ∢ = ϑ_{1} = P R_{6} Q_{1} ∢ = P Q_{6} Q_{1} ∢

, (3) és (4) alapján

ϑ_{1} = 180^{\circ} - P Q_{3} Q_{2} ∢

, végül (2) alapján

ϑ_{1} = P R_{2} Q_{2} ∢

, ami állításunkat igazolja. ‐ Hasonlóan látható be, hogy az

R_{1} R_{2} ... R_{6} = H_{2}

hatszögnek bármelyik három egymás utáni csúcsa és

P

egy kör pontjai. Pl,

P, R_{1}, R_{2}, R_{3}

és

P, R_{2}, R_{3}, R_{4}

egy-egy körön van és így a

P

-n,

R_{2}

-n,

R_{3}

-on átmenő kör átmegy

R_{1}

-en és

R_{4}

-en is. Hasonlóan látható be, hogy mind a hat pont egy körön van, amely átmegy

P

-n is.
Ezekből következik, hogy

H_{2}

bármélyik két szemközti csúcsa (amelyek indexeinek különbsége 3) a

k

egy átmérőjének két végpontja. Példaképpen

R_{2} R_{5}

-re mutatjuk meg, hogy látószöge

R_{1}

-bő1 derékszög.
Mivel

P

R_{5}

R_{6}

R_{1}

k

-n vannak, és

P Q_{6} R_{6} Q_{1}

húrnégyszög, így

P R_{1} R_{5} ∢ = ϑ_{2} = P R_{6} R_{5} ∢ = P R_{6} Q_{6} ∢ = P Q_{1} Q_{6} ∢

, és ezért

ϑ_{1}

-nek (1) alapján kapott értékével

R_{2} R_{1} R_{5} ∢ = R_{2} R_{1} P ∢ + P R_{1} R_{5} ∢ = ϑ_{1} + ϑ_{2} = P Q_{1} Q_{2} ∢ = P Q_{1} Q_{6} ∢ = Q_{2} Q_{1} Q_{6} ∢

, ami derékszög.
Most már látható, hogy

H_{1}

és

H_{2}

kapcsolata ugyanaz, mint a versenyfeladat

Q_{1} Q_{2} Q_{3} Q_{4} Q_{5} Q_{6}

és

B C A' B' C' A

hatszögeié,

H_{2}

-ből és

P

-ből a versenyfeladat szerkesztésével juthatunk el

H_{1}

-hez. Ennek felismerése feleslegessé teszi annak az állításnak a bizonyítását, hogy a feladat utolsó mondatában felsorolt szakaszok felezőpontjaival meghatározott

k'

körnek egy átmérője

O P

, mert ez már a versenyfeladatban megtörtént.

Czékus Laborc (Budapest, Toldy F. g. IV. o. t.)

Megjegyzések. 1. E bizonyítás első része a Versenyfeladat III. megoldásának megfordítása, ott a ,,

k

-beli'' húrnégyszögből (továbbá két ,,talpponti'' húrnégyszögből) bizonyítottuk

Q_{6} Q_{1}

és

Q_{2} Q_{3}

párhuzamosságát, itt pedig a párhuzamosságból azt, hogy egy négyszög csúcsai

k

-n vannak.
2. Többen a

P R_{6} R_{1} R_{2}

négyszög

P

és

R_{1}

csúcsánál levő (ábránkon szemközti) szögek összegéről mutatták meg, hogy

180^{\circ}

-kal egyenlő. Ez valamivel nehézkesebb:

R_{6} P R_{2} ∢ + R_{6} R_{1} R_{2} ∢ = R_{6} P R_{2} + Q_{1} R_{1} Q_{2} ∢ = 180^{\circ} + R_{6} P R_{2} ∢ - Q_{1} P Q_{2} ∢ = 180^{\circ} + R_{6} P Q_{1} ∢ - R_{2} P Q_{2} ∢ = 180^{\circ} + (R_{6} Q_{6} Q_{1} ∢ - R_{2} Q_{3} Q_{2} ∢) = 180^{\circ}

.
A következő megoldás más sorrendben bizonyítja az állítás egyes részeit.

II. megoldás a feladat további részére: Az

R_{1}

pont szerkesztésénél fogva

Q_{1}

és

Q_{2}

P R_{1}

átmérő fölötti

k_{1}

Thalész-kör pontjai. Messe

k_{1}

Q_{2} Q_{3}

egyenest másodszor

S

-ben, ekkor

Q_{1} S

k_{1}

-nek átmérője, mert

Q_{2}

-ből derékszögben látható. Így a

P S R_{1} Q_{1}

négyszög, amelynek csúcsait

k_{1}

két átmérőjének végpontjai adják: téglalap, ezért

P S

merőleges

P Q_{1}

-re.‐ Hasonlóan a

P R_{3}

átmérő fölötti,

Q_{3}, Q_{4}

-en átmenő

k_{3}

Thalész-körnek

Q_{2} Q_{3}

-mal való második metszéspontját

S^{*}

-gal jelölve

Q_{4} S^{*}

k_{3}

-nak átmérője, ezért

P S^{*} R_{3} Q_{4}

téglalap, és

P S^{*}

merőleges

P Q_{4}

-re. ‐ Így pedig

P S

és

P S^{*}

azonosak, mert

P Q_{4}

azonos

P Q_{1}

-gyel és

P Q_{1}

-re

P

-ben csak egy merőleges állítható. Ennélfogva

S^{*}

azonos

S

-sel, az említett két téglalapnak

P S

oldala közös. Ezért nem közös csúcsaik szintén egy téglalap csúcsait adják:

Q_{1} Q_{4} R_{3} R_{1}

téglalap.
Ugyanígy bizonyítható, hogy a

P R_{4}

és a

P R_{6}

átmérő fölé írt

k_{4}

k_{6}

Thalész-körök a

Q_{5} Q_{6}

egyenest ugyanazon

T

pontban metszik, ezért

P T R_{4} Q_{4}

és

P T R_{6} Q_{1}

, és következésképpen

Q_{1} Q_{4} R_{4} R_{6}

is téglalap. Minthogy ennek

Q_{1} Q_{4}

oldala közös az előbb téglalapnak bizonyult

Q_{1} Q_{4} R_{3} R_{1}

négyszöggel, azért

R_{1} R_{3} R_{4} R_{6}

is téglalap, köréje

k

kör írható, ebben az

R_{1} R_{4}

és

R_{3} R_{6}

átlók átmérők.
Az

R_{1} R_{4}

átmérő

P

-ből derékszögben látszik, mert egyrészt

k_{1}

-ben fellépő kerületi szögek és a

Q_{2} S | | Q_{4} Q_{5}

Q_{2} R_{3} | | Q_{5} R_{4}

párhuzamosságok folytán

S P R_{1} ∢ = 180^{\circ} - S Q_{2} R_{1} ∢ = Q_{4} Q_{5} R_{4} ∢

, másrészt a téglalap szimmetriái és

k_{4}

-beli kerületi szögek révén

T P R_{4} ∢ = P T Q_{4} ∢ = P Q_{5} Q_{4} ∢

, harmadrészt mivel a

P S R_{3} Q_{4}

és

P T R_{4} Q_{4}

téglalapok

P Q_{4}

oldala közös, tehát

S, P, T

egy egyenesen feküsznek, és így

R_{1} P R_{4} ∢ = S P T ∢ - S P R_{1} ∢ - T P R_{4} ∢ = 180^{\circ} - (Q_{4} Q_{5} R_{4} ∢ + P Q_{6} Q_{4} ∢) = 180^{\circ} - P Q_{5} R_{4} ∢ = 90^{\circ}

. (A második lépésben felhasználtuk, hogy a

k_{4}

kör

Q_{5}

-öt nem tartalmazó

P Q_{4}

és

T R_{4}

íve egyenlő.)
Ugyanígy látható be, hogy a

H_{2}

hatszög szemben fekvö

R_{4} R_{5}

és

R_{1} R_{2}

oldalai is téglalapot adnak, ennek körülírt köre is átmegy

P

-n és így azonos

k

-val, mert három pontjuk:

R_{1}, R_{4}

és

P

közös. Eszerint

k

-nak

R_{2} R_{5}

is átmérője, mert ez az utóbbi téglalapnak átlója.

Tusnády Gábor (Bp., Eötvös L. tud. egyet. term. tud. kari I. é. hallg.)

Megjegyzések. 1. Az állítás akkor is érvényes, ha a

q_{i}

egyenesek helyett azokat a

q'_{i}

, egyeneseket használjuk fel az

R'_{i}

csúcsok előállításában, amelyek átmennek a

Q_{i}

pontokon és a megfelelő

q_{i}

-hez képest ugyanazon irányban ugyanakkora hegyes szöggel el vannak fordulva. (Ez a 990. feladat első állításának megfordítása.)

Grüner György (Mosonmagyaróvár, Kossuth L. g. III. o. t. )

2. Valamennyi állítás bizonyítható koordinátageometriai úton is; ezt az utat választotta Várady Gábor (Győr, Révai M. g. IV. o. t.)