Kezdőlap


Feladat:	990. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zsolt , Benczúr András , Biborka Tamás , Bollobás Béla , Czékus Laborc , Fekete Rozália , Fritz József , Gagyi Pálffy András , Gazsi Lajos , Hajna János , Holop András , Jahn A. , Kiss Ádám , Klimó János , Kolonits Ferenc , Lendvai Katalin , Mezey Ferenc , Mihályffy L. , Molnár Emil , Náray Szabó G. , Palágyi F. , Pinkert A. , Sonnevend Gy. , Tihanyi Ambrus , Tusnády Gábor
Füzet:	1960/április, 112 - 114. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Forgatva nyújtás, Simson-egyenes, Egyéb sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1959/szeptember: 990. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. 1. Legyen az elforgatás szöge $φ$ , és legyenek az új módon keletkezett hatszög csúcsai 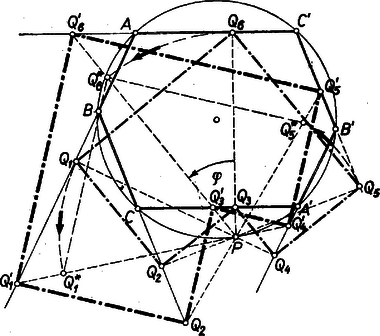$Q'_{1}, Q'_{2}, ..., Q'_{6}$ .

1. ábra

Ekkor a

P Q'_{i} Q'_{i}

háromszögek derékszögűek

(i = 1,2, ...,6)

, bennük

Q'_{i} P Q_{i} ∢ = φ

, ennélfogva

P Q'_{i} = P Q_{i} / cos φ

, vagyis

Q'_{i}

-t

Q_{i}

-ből (a közvetlen szerkesztés helyett transzformációval,

P

középpontú,

φ

szögű,

1 / cos φ

nyújtási arányszámú forgatva nyújtással is megkaphatjuk. Idomokra nézve a forgatva nyújtás hasonlósági transzformáció; mert a nyújtás ilyen, és az egy idomból puszta forgatással előálló, vele egybevágó idom is tekinthető az eredetihez hasonlónak,

1 : 1

arányú nyújtással; ha pedig a

J_{1}, J_{2}

és

J_{2}, J_{3}

idompárok között hasonlóság áll fenn, akkor

J_{1}

, és

J_{3}

is hasonlók. Ezért a

Q'_{1} Q'_{2} Q'_{3} Q'_{4} Q'_{5} Q'_{6} = H'

hatszög hasonló a

Q_{1} Q_{2} Q_{3} Q_{4} Q_{5} Q_{6} = H

-hoz, tehát szögeik egyenlők, és így

H'

-nek is bármely két szomszédos oldala merőlegesen áll egymásra.

I. 2. A versenytétel bizonyításában nem használtuk fel az

A B C A' B' C'

hatszög konvex voltát, ezért az ott adott bizonyítások hurkolt hatszög esetére is érvényesek; és csak aszerint mutatnak egymástól kis jelölésbeli eltéréseket, hogy a hurkolt hatszögnek mely oldalai metszik egymást, továbbá hogy

P

a körnek melyik ívén fekszik. Példaképpen megmutatjuk, hogy a 2. ábrán látható helyzet

ω = Q_{1} Q_{2} Q_{3}

szöge derékszög.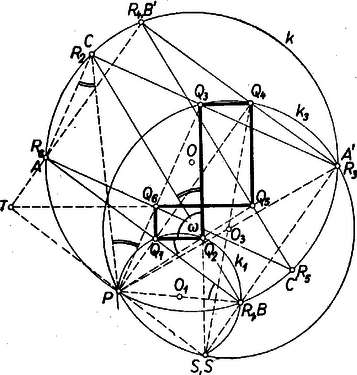

2. ábra

Ehhez elég belátni, hogy

ω

és a szerkesztéssel képezett

P Q_{2} C

derékszög közös

Q_{1} Q_{2} C

részét elhagyva, a

P Q_{2} Q_{1}

és

C Q_{2} Q_{3}

szögek egyenlők. A

P, Q_{2}, Q_{1}

pontok és

B

Q_{2}, Q_{1}

-et tartalmazó hatszögoldalak közös csúcsa) szerkesztésnél fogva egy húrnégyszög csúcsai, ezért

P Q_{2} Q_{1} ∢ = P B Q_{1} ∢ = P B A ∢

, és hasonlóan a

P Q_{2} Q_{3} C

húrnégyszögből

C Q_{2} Q_{3} ∢ = C P Q_{3} ∢

Az utóbbi szög egyenlő a

P C A

szöggel, mert váltószögek, ugyanis Thalész tétele folytán

A C

merőleges

A' C

-re és így párhuzamos

P Q_{3}

-mal. Végül a

P B A

és

P C A

szögek egyenlők, mert

P

A, B, C

pontokkal meghatározott körön fekszik. Ezzel a tervbe vett bizonyítást befejeztük.

II. E bizonyításban csak az

A A'

átlóról használtuk fel, hogy

k

-nak átmérője (

B', C',

nem szerepelt) és ezt használjuk ki a

Q_{5}

-nél fekvő szög esetében is. Hasonlóan a

Q_{3}

és

Q_{6}

csúcsnál fekvő szögek derékszög volta csak a

B B'

átlónak átmérő voltára támaszkodik, a

Q_{4}

és

Q_{1}

-nél fekvőké pedig csak

C C'

-nek átmérő voltára.
Ha már most

A A'

nem átmérő, akkor

ω

nem derékszög; ezt az előbbi bizonyításhoz kapcsolódva bizonyítjuk (3. ábra).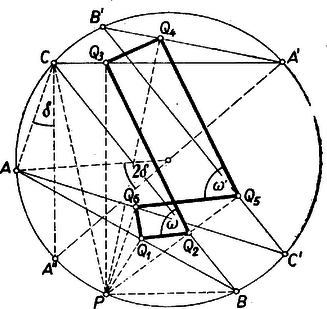

3. ábra

Legyen az

A'

-n átmenő átmérő másik végpontja

A''

. Most

C A

nem merőleges

C A'

-re, hanem az erre merőlegesen álló

C A''

-vel akkora

δ

szöget zár be, mint az

A O A''

szög fele, ahol

O

k

kör középpontja. Eszerint a

P Q_{2} Q_{1}

és

C Q_{2} Q_{3}

szögek eltérése is

δ

, és így

ω

P Q_{2} C

derékszögnél

δ

-val kisebb vagy nagyobb. Hasonlóan látható be, hogy az

ω' = Q_{4} Q_{5} Q_{6}

szög is

δ

-val tér el a derékszögtől. (Az ábrán

ω' = ω

; más helyzetben

ω + ω' = 180^{\circ}

is lehetséges.) Konvex hatszögből kiindulva is hasonlóan halad a bizonyítás. Ezek szerint

H

-nak annyiszor két szöge tér el a derékszögtől, ahány átló az

A A', B B', C C'

közül nem átmérője a körnek. Ezzel a feladat állításait bebizonyítottuk.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

Megjegyzések. 1. Több dolgozat használta fel bizonyítás nélkül az ún. Simson-egyenesek tételét, holott azt a fentiekhez hasonlóan könnyen bebizonyíthatta volna. A tétel a következő: az

A B C

háromszög

k

körülírt körén felvett tetszés szerinti

P

pontból az

A B, B C, C A

oldalakra bocsátott merőlegesek talppontjai egy egyenesen, az

A B C

háromszöghöz és a

P

ponthoz tartozó Simson-egyenesen feküsznek.
2. Két dolgozat szerint ha az eredeti hatszög hurkolt, akkor a

Q

-hatszög is ilyen. Ez nem szükségszerű.