Feladat: 989. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Czékus Laborc ,  Fritz József ,  Gazsi Lajos ,  Hahn János ,  Muszbek László ,  Rozváczy Judit ,  Tihanyi Ambrus 
Füzet: 1960/április, 109 - 112. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Vetítések, Trigonometriai azonosságok, Húrnégyszögek, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1959/szeptember: 989. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tegyük fel, hogy van a feladatban leírt tulajdonságú M pont és vegyük segítségül az AD oldalnak azt az N pontját, amelyre AN=AB; ekkor azt kell bizonyítanunk, hogy 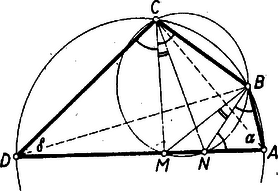CD=DN.

 
 

Legyen BAD∢=α és CDA∢=δ, ekkor a húrnégyszög szögeire vonatkozó tétel alapján BCD∢=180∘-α és ABC∢=180∘-δ. Az adott tulajdonságú M pont rajta van a négyszög B,C csúcsainál fekvő szögek felezőin, ezért ABM∢=(180∘-δ)/2 és BCM∢=(180∘-α)/2. Az utóbbi szög akkora, mint az ABN egyenlő szárú háromszög alapján fekvő ABN és ANB szögek, így a BCMN idom húrnégyszög és N a BCM háromszög körülírt körének AD-vel való második közös pontja. Most már ‐ feltéve, hogy N az AM szakaszon van ‐
NCD∢=NCM∢+MCD∢=NBM∢+BCM∢==(ABM∢-ABN∢)+BCM∢=ABM∢=(180∘-δ)/2,


vagyis az NCD háromszög egyenlő szárú, CD=ND, amit bizonyítani akartunk. ‐ Ha N a DM szakasz pontja, akkor ismét
NCD∢=MCD∢-MCN∢=BCM∢-MBN∢==BCM∢-(ABN∢-ABM∢)=ABM∢.


Végül ha N egybeesik M-mel, akkor ABM∢=ABN∢=(180∘-α)/2, így ABC∢=2ABM∢=180∘-α, vagyis BC párhuzamos AD -vel, az ABCD négyszög szimmetrikus trapéz, ezért az M≡N pont a szimmetriatengelyen van, tehát felezi AD-t, és így DN=AN=AB=CD. Ezzel a bizonyítást befejeztük.
 

Czékus Laborc (Budapest, Toldy F. g. IV. o. t.)

 

Megjegyzések. 1. Az AB+CD=AD feltétel elegendő is a kérdéses tulajdonságú M pont létezéséhez. Ha ugyanis egy kör AD húrjának egy pontja N és a kört az A körül AN, és D körül DN sugárral írt körök AD-nek ugyanazon oldalán B, ill. C-ben metszik, akkor van az AD húron olyan pont, amely az ABCD négyszög AB,BC és CD oldalaitól egyenlő távolságra van. Ilyen a BCN háromszög köré írt körnek AD-vel való M második metszéspontja, (ill. ha e kör érinti AD-t, akkor maga N). Valóban, a fenti jelöléseket használva, és csupán arra az esetre szorítkozva, ha M a DN szakaszon adódik: MBA∢=180∘-α-ABM∢=DCB∢-NMB∢=DCB∢-NCB∢=DCN∢=(180∘-δ)/2=ABC∢/2, vagyis BM felezi az ABC szöget, M egyenlő távolságra van AB és BC-től. (Csak C és M szerkesztési módját használtuk fel, továbbá B-ről azt, hogy valahol a körnek az ADC szög szárai közötti AC ívén van.) Hasonlóan látható be, hogy CM felezi a DCB szöget és így M egyenlő távolságra van BC és CD-től; ebben használjuk fel B szerkesztési módját. Eszerint M mindhárom mondott oldaltól egyenlő távolságra van.
2. Sem az állítás, sem a megfordított tétel bizonyításában nem használtuk fel, hogy AD a körülírt körben átmérő, ezért minden olyan konvex húrnégyszögben, amelyben két szomszédos szög felezői egymást a csúcsaikat összekötő oldallal szemközti oldalon metszik, ez a szemben fekvő oldal egyenlő a vele szomszédos oldalak összegével. Az ABCD idom konvexségét viszont felhasználtuk, vagyis hogy B és C az AD-nek ugyanazon partján vannak, ezen alapult a BCM háromszög körülírt körében az MN húr C és B-ből való látószögeinek egyenlősége.
 

Gazsi Lajos (Kaposvár, Táncsics M. g. IV. o. t.)

Tihanyi Ambrus (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

 

A további megoldások ábráin AD nem átmérőnek van rajzolva, de a szövegben nem térünk ki azon esetekre, ha α és δ között tompaszög is lép fel.
 

II. megoldás: Legyen M vetülete az AB,BC,CD oldalon rendre E, F, G, ekkor feltevésünk szerint ME=MF=MG, továbbá BE=BF és CF=CG. Így az MEBF és MFCG négyszögek húrdeltoidok, EF és MB, ill. FG és MC átlóik merőlegesek, és bennük, az ABCD idom húrnégyszög voltát is felhasználva, EMF∢=180∘-EBF∢=180∘-ABC∢=ADC∢=δ és hasonlóan FMG∢=α. Ezért ha még E és G vetülete MF-re H, ill. J, akkor az MGJ és AME, valamint MEH és DMG derékszögű háromszögek hasonlók és ugyanez áll a merőleges szárú δ/2 ill. α/2 hegyesszögeket tartalmazó MBF, EFM és MCF, GFJ derékszögű háromszög-párokra. Ezek alapján folytatólagos átalakítása,
EBME=FBMF=HFEH=MFEH-MHEH=MEEH-DGMG=DMMG-DGMG=DM-DGME,
és így (az egyenlőség-sorozat szélső tagjait ME-vel szorozva) EB=DM-DG, másképpen EB+GD=MD. Hasonlóan kapjuk, hogy AE+CG=AM (A és D-t, B és C-t páronként felcserélve E és G, valamint H és J is páronként felcserélődnek.) E két egyenlőség alapján pedig
AB+CD=(AE+EB)+(CG+GD)=(AE+CG)+(EB+GD)==AM+MD=AD,


amit bizonyítanunk kellett.
 

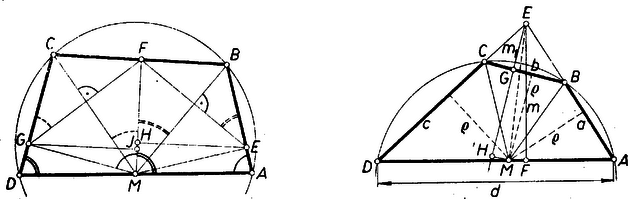Hahn János (Szeged, Déry M. gépip. t. IV. o. t.)

 
 

III. megoldás: Legyenek a négyszög oldalai AB=a, BC=b, CD=c, DA=d, a kérdéses M pontnak a három oldaltól való távolsága ϱ, az AB és DC oldalegyenesek metszéspontja E, ennek vetülete AD és BC-re F, ill. G, és EF=m, EG=m1. A feltevésnél fogva EM felezi az AED szöget. Így az ABCD négyszög kétszeres területe kétféleképpen is kifejezhető:
2t=(a+b+c)ϱ=dm-bm1,
és innen
AB+CD=a+c=dm-b(m1+ϱ)ϱ.
Az ADE és CBE háromszögek hasonlók, mert a C és A, a B és D csúcspároknál fekvő szögeik a húrnégyszög alaptulajdonsága folytán egyenlők, így b:d=m1:m, b=dm1/m, ennélfogva
a+c=dm2-dm1(m1+ϱ)mϱ.
Ugyancsak a fenti indok alapján hasonlóak az AEF és CEG derékszögű háromszögek is, így EF és EG tükrös párok EM-re. Ha tehát az M-en át BC-vel húzott párhuzamos EG-t H-ban metszi, akkor HG=ϱ, továbbá az MEH és MEF derékszögű háromszögek egybevágóságából
EH=EG+GH=m1+ϱ=EF=m,másképpenm-m1=ϱ,
és ennek felhasználásával
a+c=dm2-dm1mmϱ=dm-dm1ϱ=d(m-m1)ϱ=d,
amit bizonyítanunk kellett.
 

Rozváczy Judit (Budapest, Szilágyi Erzsébet lg. II. o. t.)

 

Megjegyzések. 1. A négyszög területének kifejezéséhez átmenetileg trigonometriai ismereteket is használva hasonlóan juthatunk célhoz. A kétszeres terület az AC átlóval való két részre osztásból kiindulva
2t=absin(180∘-δ)+cdsinδ=(ab+cd)sinδ=(ab+cd)ϱ/DM,
és innen DM=(ab+cd)ϱ/2t. Hasonlóan a BD átlóval való felbontásból AM=(ad+bc)ϱ/2t. Ezekkel AM+DM=d alapján, valamint a fenti megoldás kiindulópontjának felhasználásával
2t/ϱ=(ab+cd+ad+bc)/d=a+b+c
és innen átrendezéssel a+c=d.
 

Muszbek László (Törökszentmiklós, Bercsényi M. g. IV. o. t.)
 

2. A megoldások többsége trigonometriai úton bizonyította az állítást. Ilyen volt a II. megoldás is, amely alapgondolatában a tgx/2=(1-cosx)/sinx azonosságot használta fel. Ajánljuk a megoldás ilyen átalakítását és az összehasonlítást. Utolsóként egy szögfüggvényeket felhasználó megoldást adunk, ebben egyszerűség végett támaszkodunk arra, hogy AD átmérő, és hogy 0∘<α, δ<90∘.
 

IV. megoldás: Feltevésünk úgy is kimondható, hogy a négyszögünk B és C csúcsánál fekvő szögek felezői AD-n metszik egymást. Ez a félkörbe írt négyszögek közül nyilván nem valamennyire teljesül (pl. az AD alapon álló elég kicsi és elég nagy magasságú egyenlő szárú trapézekben a metszéspont ,,közel van'' az AD-re merőleges átmérő ,,alsó'', ill. ,,felső'' végpontjához), ezért avégett, hogy a szögfelezők AD-n messék egymást, B és C közül, más szóval α és δ közül legfeljebb az egyiket választhatjuk tetszés szerint. Keressünk tehát összefüggést α és δ között. Az ABD és ACD derékszögű háromszögekből AB=ADcosα, CD=ADcosδ, ezért a bizonyítandó egyenlőségből AD-vel való osztással ez várható: cosα+cosδ=1.
Ezt abból bizonyítjuk, hogy 1/AM-nek az AMB és AMC háromszögekből a szinusz-tétel alapján vett kifejezései egyenlők. Az ABM háromszögből ABM∢=90∘-δ/2, így AMB∢=180∘-α-(90∘-δ/2)=90∘-(α-δ/2); másrészt ACB∢=DCB∢-DCA∢=180∘-α-90∘=90∘-α, így MCA∢=MCB∢-ACB∢=(180∘-α)/2-(90∘-α)=α/2, tehát az ACM háromszögből AMC∢=180∘-(90∘-δ)-α/2=90∘+(δ-α/2). Ezekkel
1AM=sinAMB∢ABsinABM∢=sinAMC∢ACsinACM∢,cos(α-δ/2)ADcosαcosδ/2=cos(δ-α/2)ADsinδsinα/2.


A számlálókat az addició tételek alapján felbontva és tagonkénti osztással, egyszerűsítéssel
1+sinαsinδ/2cosαcosδ/2=cosδcosα/2sinδsinα/2+1.
Átrendezéssel, a sinx=2sinx/2cosx/2, majd a 2sin2x/2=1-cosx azonosságok alapján
4sin2α/2sin2δ/2=cosαcosδ,(1-cosα)(1-cosδ)=cosαcosδ,1-cosα-cosδ=0,


amit bizonyítani akartunk.
 

Fritz József (Mosonmagyaróvár, Kossuth L. g. III. o. t.)

 

Megjegyzés. Számos dolgozat azért hiányos, mert szűk, a helyzetekbe mindenáron szimmetriát bevinni kívánó (többnyire öntudatlan) szemléletből kiindulva az ABCD négyszög egyetlen lehetséges alakjaként a szabályos hatszög felét hajlandó elfogadni, vagy ami ugyanaz, M-et csak AD felezőpontjaként. Az I. megoldásból látható, hogy az AD húron bárhol felvett N pontból kiindulva AB=AN és DC=DN-nel és B, C-t AD-nek ugyanazon partján véve a szóbanforgó tulajdonságú négyszöget kapunk.