Kezdőlap


Feladat:	983. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Biborka T. , Bollobás B. , Csanak Gy. , Czékus L. , Fejes L. , Flanek L. , Hajna J. , Halász G. , Kiss Ádám , Klimó J. , Kohut M. , Kolonits F. , Losonczi L. , Máté A. , Máté Zs. , Mezey F. , Mihályffy L. , Molnár E. , Nagy Ákos , Náray M. , Parti Enikő , S. Nagy Erzsébet , Szücs J. , Tihanyi A. , Várady G.
Füzet:	1960/április, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Tengely körüli forgatás, Térfogat, Szabályos sokszögek által határolt testek, Térgeometriai bizonyítások, Szabályos tetraéder, Feladat
Hivatkozás(ok):	Feladatok: 1959/május: 983. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A felhajtás, más szóval (legfeljebb $180^{\circ}$ -nyi) forgatás közben a hatszög-lapoknak bármely, nem a forgatási élbe, a $t$ tengelybe eső $P$ pontja olyan félkört ír le, melynek síkja merőleges a tengelyre és középpontja $P$ forgatás előtti helyzetének a $t$ -n levő $P_{0}$ vetülete. Minden ilyen félkörnek az $A B C$ háromszög (helyben maradó) $S$ síkjára való vetülete a $t$ -re merőleges $2 P P_{0}$ hosszúságú szakasz, felezőpontja $P_{0}$ . ‐ A szabályos háromszög és a szabályos hatszög egy-egy szögének összege $180^{\circ}$ , ezért a hatszögek $D_{2}, E_{1}$ ; $E_{2}, F_{1}$ ; $F_{2}, D_{1}$ csúcsai (a felhajtások előtt) az $A B, B C, C A$ tengelyek meghosszabbításainak pontjai, továbbá az oldalak egyenlősége folytán az $A D_{2} D_{1} = H_{1}$ , $B E_{2} E_{1} = H_{2}$ , $C F_{2} F_{1} = H_{3}$ háromszögek a oldalú szabályos háromszögek, és így $G, D_{1}, D_{2}, M$ is egy egyenes pontjai.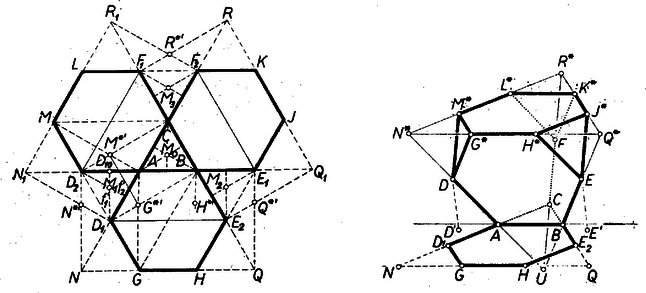
Ezek szerint a $D_{1}$ csúcs által leírt $f_{1}$ félkör vetülete a $H_{1}$ -nek $D_{1}$ -ből húzott magasságvonalára esik, és hasonlóan $D_{2}$ pályájának, $f_{2}$ -nek vetülete a $D_{2}$ -ből húzott magasságvonalra. Ezek egyetlen közös pontja $H_{1}$ -nek $M_{1}$ magasságpontja, és ez az említett szakaszoknak is pontja. Ennélfogva $f_{1}$ és $f_{2}$ -nek a feladatban szereplő $D$ egybeesési pontja egyértelműen létezik, vetülete $M_{1}$ .
A hatszöglapok $D_{1} E_{2}$ , $D_{2} F_{1}$ , átlói a forgatás minden helyzetében párhuzamosak az $A B$ , ill. $A C$ tengellyel (ezért $S$ -sel is), és ugyanez áll $S$ -en levő vetületükre. Ebből ábránk szimmetriaviszonyainak figyelembevételével nyilvánvaló, hogy amikor $D_{1}$ és $D_{2}$ a $D$ -ben egybeesnek, akkor $E_{2}$ , ill. $F_{1}$ vetülete $H_{2}$ -nek $M_{2}$ , ill. $H_{3}$ -nak $M_{3}$ magasságpontjába esik. Ugyanezért a második hatszög forgatása közben $E_{1}$ egybeesik az első és harmadik hatszög rögzítése folytán rögzített $E_{2}$ -vel, és ekkor $F_{2}$ is egybeesik a rögzített $F_{1}$ -gyel. Ezzel az állítás első részét bebizonyítottuk. A $D E F = S_{1}$ sík, párhuzamos $S$ -sel, mert egymást metsző $D E, D F$ egyenesei párhuzamosak $S$ -sel.
A $G H$ él az első hatszöglap bármely helyzetében párhuzamos $S$ -sel, és ‐ mint a forgatás előtt is ‐ kétszer akkora távolságra van $A B$ -től, mint $D_{1} E_{2}$ . Ezért $G$ és $H$ a lap rögzítésével abba az $S$ -sel párhuzamos $S_{2}$ síkba jut, amely kétszer akkora távolságban van $S$ -től, mint $S_{1}$ , $S$ -nek ugyanazon oldalán, mint $S_{1}$ . Ugyanez áll a felhajlított $J, K, L, M$ -re. Ezzel a kívánt bizonyítást befejeztük; ki kell még számítanunk a keletkezett $P$ konvex test térfogatát.

Legyenek a lapok szabadon álló csúcsai a felhajlítás után

G^{*}, H^{*}, ..., M^{*}

. Ekkor

P

-t ,,felülről'' nyilván a

G^{*} H^{*} ... M^{*}

hatszög határolja, és további lapjai a

D G^{*} M^{*}

E H^{*} J^{*}

F K^{*} L^{*}

háromszögek. Az

A D_{2} D_{1}

, és

B D_{2} G

háromszögek hasonlósága folytán

G^{*}

-nak

G^{*}'

vetülete a

B D_{2} G

háromszög magasságpontjába esik, és ugyanígy

M^{*}

-nak

M^{*}'

vetülete a

C M D_{1}

háromszög magasságpontjába. Így

G^{*} M^{*}

párhuzamos és egyenlő

G^{*}' M^{*}'

-vel, ez pedig

B C (= a)

-val, mert az utóbbi két

2 a

oldalú szabályos háromszög egybevágó és

D_{1} D_{2}

oldalszakaszuk közös, így a

G^{*}' M^{*}' C B

négyszög paralelogramma, ‐ továbbá

H^{*} G^{*} M^{*} ∢ = E_{1} B C ∢ = 120^{\circ}

. Ezek szerint

G^{*} H^{*} ... M^{*}

ugyancsak

a

-oldalú szabályos hatszög,

P

további három lapja pedig

a

oldalú szabályos háromszög, vagyis

P

-t négy

a

oldalú szabályos hatszög és négy

a

oldalú szabályos háromszög határolja, minden csúcsában két hatszög és egy háromszög síkja metszi egymást.
Ebből nyilvánvaló, hogy ha az első hatszög

G H

oldalának

A D_{1}

B E_{2}

-vel való metszéspontját

N, Q

-val jelöljük, e lap helyett a

3 a

oldalú

N Q C

háromszöget forgatjuk míg

D_{1}

D

-be jut, és ezen lépéseink megfelelőit a másik két hatszöglapban is elvégezzük

(Q R A

és

R N B)

, akkor e három lap egy felül nyitott,

3 a

élű

N^{*} Q^{*} R^{*} U = T

szabályos tetraédert határoz meg. A

G^{*} H^{*} ... M^{*}

-ből hasonlóan keletkező

N^{*} Q^{*} R^{*}

háromszög lezárja

T

-t. (

C

A B

tengelynek a hatszöggel ellentétes partján fekszik, így a

C A B

kiegészítő háromszög

S

alá fordul, az elforduló

C, A, B

csúcsok

S

alatt esnek egybe

U

-ban, ennek

S

-en való vetülete az

A B C

háromszög

M_{0}

magasságpontja.

T

éleit

P

csúcsai

3 - 3

egyenlő részre osztják, ezért

T

-ből

P

-t négy egybevágó,

a

élű szabályos tetraéder lemetszésével kapjuk (egyikük

N^{*} G^{*} M^{*} D

). Minthogy a

b

élű szabályos tetraéder térfogata

b^{3} \sqrt[]{2} / 12

, azért

P

térfogata

\begin{matrix} V = \frac{\sqrt[]{2}}{12} [{(3 a)}^{3} - 4 a^{3}] = \frac{23 \sqrt[]{2} a^{3}}{12} . \end{matrix}

P

-nek mind a 12 csúcsa egyenértékű, minden csúcsban 3 lap: 2 hatszög és 1 háromszöglap fut össze. Eszerint bármelyik csúcsból 3 él indul ki és

2 \cdot 3

lapbeli átló az ide befutó hatszögekben. Így a csúcsból a további 11 csúcs közül 9-hez nem testátló vezet, tehát csúcsonként 2 testátló indul ki, pl.

A

-ból

J^{*}

és

K^{*}

-ba. Eszerint a testátlók összes száma 12, mert a kiindulások száma

12 \cdot 2

, de minden átlón két kiindulási pont van.

S. Nagy Erzsébet (Makó, József A. g. IV. o. t)

Megjegyzés. Hogy

G^{*} M^{*} = a

, azt így is beláthatjuk: a hatszöglapok

ϑ

elfordulási szögére

cos ϑ = D_{10} M_{1} / D_{10} D_{1} = 1 / 3

, így

A G^{*}' = A G / 3

A M^{*}' = A M / 3

, ezért az

A

-nál közös szögű

A G^{*}' M^{*}'

és

A G M

háromszögek hasonlók:

G^{*}' M^{*}' = G M / 3 = a

Parti Enikő (Budapest, Bagi Ilona lg. III. o. t.)