Kezdőlap


Feladat:	982. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alpár A. , Arató Péter , Bollobás B. , Czékus L. , Gazsó Erzsébet , Hadik Z. , Hajna J. , Halász G. , Hegedüs I. , Holop A. , Horváth Árpád , Jahn É. , Kiss Ádám , Klimó J. , Kolonits Ferenc , Komlóssy Gy. , Marót Ildikó , Máté A. , Máté Zs. , Mészáros Kornélia , Mezey F. , Mihályffy L. , Molnár E. , Náray M. , Náray Szabó G. , Parti Enikő , Pósch Margit , S. Nagy Erzsébet , Sós T. , Szücs J. , Tihanyi A. , Várady G. , Zeke A.
Füzet:	1960/április, 97 - 100. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Pont körüli forgatás, Számtani-mértani egyenlőtlenségek, Négyzetek, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1959/május: 982. matematika feladat

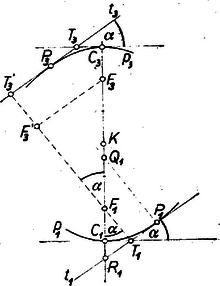
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az N alakzat létezik, mert a $p_{1}$ parabola $C_{1}$ csúcsa az origó, tengelye az $Y$ -tengely, paramétere 2 egység, fókusza $F_{1} (0; 1)$ így az adott $K$ pont a $p_{1}$ belsejében van ‐ nem magán a parabolán ‐ ezért $K$ a $p_{2}, p_{3}, p_{4}$ -nek is a belsejében van és ugyanez áll egy a $K$ körül elég kicsi sugárral írt kör minden pontjára, tehát a négy parabola belsejének van közös része.
Ha N-nek egy a $p_{1}$ -ből való kerületi pontjában a támaszegyenese $t_{1}$ , akkor az ebből a $K$ körüli forgatásokkal előálló $t_{2}, t_{3}, t_{4}$ egyenes ugyancsak támaszegyenes, másrészt ezek egy négyzetet zárnak körül, tehát N négyzetekkel burkolható.
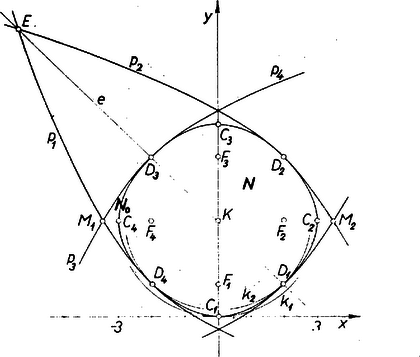
A legnagyobb és a legkisebb támasznégyzet meghatározása céljára le kell írnunk N-et. $p_{2}, p_{3}, p_{4}$ csúcsa rendre a $C_{2} (3; 3), C_{3} (0; 6), C_{4} (- 3; 3)$ pont, fókuszaik $F_{2} (2; 3), F_{3} (0; 5), F_{4} (- 2; 3)$ , egyenleteik: ${(y - 3)}^{2} + 4 (x - 3) = 0$ , $x^{2} + 4 (y - 6) = 0$ , ${(y - 3)}^{2} - 4 (x + 3) = 0$ . $p_{1}$ és $p_{3}$ egymást az $M_{1} (- \sqrt[]{12}; 3)$ és $M_{2} (\sqrt[]{12}; 3)$ pontokban metszik, belsejük közös része a (lencse alakú) $N_{0} = M_{1} C_{1} M_{2} C_{2} M_{1}$ görbevonalú idom, N-et csak ebben kereshetjük. $C_{2}$ és $C_{4}$ az $M_{1} M_{2}$ szakaszon vannak, tehát $N_{0}$ -ban, eszerint N úgy keletkezik $N_{0}$ -ból, hogy $p_{2}$ és $p_{4}$ -nek $C_{2}$ -t, $C_{4}$ -et tartalmazó bizonyos ívei $N_{0}$ -nak bizonyos részeit levágják. Szimmetria okokból, minthogy $K$ rajta van $p_{1}$ és így mindnégy parabola tengelyén, elég lesz meghatároznunk $p_{2}$ közös pontját $p_{1}$ -nek $M_{1} C_{1} M_{2}$ ívével, amelyen fekvő pontok abszcisszáira $- \sqrt[]{12} \leq x \leq \sqrt[]{12} .$
E célra alább megmutatjuk, hogy $p_{2}$ a $p_{1}$ -nek tükörképe a $K$ -n átmenő, az $Y$ -tengellyel $+ 45^{\circ}$ -ot bezáró $e$ egyenesre, melynek egyenlete: $y = - x + 3$ . Így $p_{1}$ -nek és $e$ -nek könnyen kiszámítható $D_{1} (2; 1)$ és $E (- 6; 9)$ metszéspontjai $p_{2}$ is rajta vannak. Más közös pontja nincs is $p_{1}$ és $p_{2}$ -nek, mert az egyenletükből összekapcsolt egyenletrendszer $y$ kiküszöbölésével az $x^{4} - 24 x^{2} + 64 x - 48 = 0$ egyenletre vezet, és ennek nincs más gyöke, mint $D_{1}$ és $E$ abszcisszája (az előbbié háromszoros gyök). ‐ $E$ nincs rajta az $M_{1} C_{1} M_{2}$ íven, $D_{1}$ viszont rajta van, ennélfogva $p_{2}$ -nek az az íve, amely $N_{0}$ -nak N-be nem tartozó részét levágja, $D_{1}$ -ből indul ki. Végpontja pedig $p_{2}$ és $p_{3}$ -nak a $D_{1}$ -ből a $K$ körüli $90^{\circ}$ -os forgatással is előálló közös pontja: $D_{2} (2; 5)$ , mert $p_{3}$ a $p_{2}$ ből is előáll, ha azt $K$ körül $90^{\circ}$ -kal elforgatjuk. Hasonlóan $p_{4}$ a $p_{2}$ -böl $K$ körüli $180^{\circ}$ -os forgatással is előáll, ezért $p_{4}$ fent említett ívének végpontjai a $D_{3} (- 2; 5)$ és $D_{4} (- 2; 1)$ pontok.

p_{2}

valóban tükörképe

p_{1}

-nek

e

-re, mert a

p_{2}

-t előállító

90^{\circ}

-os forgatást helyettesíthetjük két a

K

-n átmenő, egymással

45^{\circ}

szöget bezáró tengelyen alkalmas sorrendben való tükrözéssel.^{$^{*}$} Első tengelynek az

Y

-tengelyt véve, ‐ mert ez

p_{1}

-et önmagába viszi át ‐ a második tengely

e

lesz, ‐ amint állítottuk. ‐ Mindezek szerint N-nek nemcsak forgási, hanem tengelyes szimmetriái is vannak, tengelyei a páronként egybeeső parabolatengelyek és szögfelezőik:

e

és a

K

-n át

e

-re merőleges egyenes. ‐

p_{1}

-nek

D_{1}

, beli

d_{1}

érintője

p_{2}

-t is érinti ugyanitt, mert egyenlete

2 (y + 1) - 2 x = 0

, azaz

y = x - 1

, iránytényezője

m = 1

, és így merőleges

e

-re, a tükrözéssel önmagába megy át. Eszerint N-nek

D_{1}

-ben nincs csúcsa, támaszegyenese egyértelműen

d_{1}

, továbbá az ebből forgatással előálló

d_{2}, d_{3}, d_{4}

-et leszámítva minden támaszegyenese érintője a megfelelő parabolaívnek.
Alább megmutatjuk, hogy N köré és bele

K

-val mint középpónttal kör írható, vagyis van olyan

k_{1}

ill.

k_{2}

kör, amelynek vannak közös pontjai N határvonalával, és

k_{1}

, magába foglalja N-et, N magába foglalja

k_{2}

-t.

k_{1}

a parabolák

C

csúcsain megy át,

k_{2}

pedig az ívek

D

csatlakozási pontjain, tehát sugaruk

3

, ill.

2 \sqrt[]{2}

egység, így

k_{1}, k_{2}

minden támasznégyzetének oldala

6

, ill.

4 \sqrt[]{2}

egység. N-nek nem lehet nagyobb támasznégyzete, mint

k_{1}

-nek, mert

k_{1}

minden támasznégyzete magába foglalja N-t; 6 egységnyi oldalú támasznégyzete viszont van: az, amelyben a fenti

t_{1}

, az

X

-tengely, tehát N legnagyobb támasznégyzetének oldala

6

egységnyi. És N-nek nem lehet kisebb támasznégyzete, mint

k_{2}

-nek, mert minden támasznégyzete magába foglalja

k_{2}

-t,

4 \sqrt[]{2}

oldalú támasznégyzete pedig van: az, amelyben

t_{1}

azonos

d_{1}

-gyel, tehát N legkisebb támasznégyzetének oldala

4 \sqrt[]{2}

egységnyi.
Valóban, a

p_{1}

parabola

D_{4} D_{1}

ívének minden

(x_{0}, y_{0})

, azaz

(x_{0}, x_{0}^{2} / 4)

pontja, amelyre tehát

\begin{matrix} - 2 ≦ x_{0} ≦ 2, \end{matrix}

k_{1}

és

k_{2}

között, vagy egyikükön van, ‐ és ezért ugyanez áll N határvonalának

D_{1} D_{2}

D_{2} D_{3}

D_{3} D_{4}

íveire. Ugyanis

k_{1}, k_{2}

egyenlete

x^{2} + {(y - 3)}^{2} = 9

, ill.

x^{2} + {(y - 3)}^{2} = 8

, így alsó félkörívük

x_{0}

abszcisszájú pontjának ordinátája

\begin{matrix} y_{1} = 3 - \sqrt[]{9 - x_{0}^{2}}, ill. y_{2} = 3 - \sqrt[]{8 - x_{0}^{2}}, \end{matrix}

így azt kell belátnunk, hogy ezekkel teljesül

y_{1} ≦ y_{0} ≦ y_{2}

, azaz

\begin{matrix} 3 - \sqrt[]{9 - x_{0}^{2}} ≦ \frac{x_{0}^{2}}{4} ≦ 3 - \sqrt[]{8 - x_{0}^{2}} . \end{matrix}

Evégett megkeressük, hogy ez a kettős egyenlőtlenség ‐

\sqrt[]{8} ≦ x_{0} ≦ \sqrt[]{8}

értelmezési tartományának mely

x_{0}

számaira teljesül. Az átrendezéssel adódó

\begin{matrix} 3 - \frac{x_{0}^{2}}{4} ≦ \sqrt[]{9 - x_{0}^{2}}, \sqrt[]{8 - x_{0}^{2}} ≦ 3 - \frac{x_{0}^{2}}{4} \end{matrix}

egyenlőtlenségekben a kisebb oldal sem negatív, ezért négyzetükre ugyanazon irányú egyenlőtlenség áll:

\begin{matrix} - \frac{3 x_{0}^{2}}{2} + \frac{x_{0}^{4}}{16} ≦ - x_{0}^{2}, - x_{0}^{2} ≦ 1 - \frac{3 x_{0}^{2}}{2} + \frac{x_{0}^{4}}{16}, \end{matrix}

azaz

\begin{matrix} 0 ≦ \frac{x_{0}^{2}}{2} (1 - \frac{x_{0}^{2}}{8}), 0 ≦ 1 - \frac{x_{0}^{2}}{2} + \frac{x_{0}^{4}}{16} = {(1 - \frac{x_{0}^{2}}{4})}^{2}, \end{matrix}

ez pedig akkor teljesül, ha

\begin{matrix} x_{0}^{2} ≦ 8, - 2 \sqrt[]{2} ≦ x_{0} ≦ 2 \sqrt[]{2}, ill. x_{0}^{2} ≦ 4, - 2 ≦ x_{0} ≦ 2, \end{matrix}

vagyis a

D_{4} D_{1}

ív minden pontjára. Egyenlőség csak az

x_{0} = 0

, ill. az

x_{0} = \pm 2

abszcisszák mellett teljesül, vagyis

C_{1}

-re, ill.

D_{4}

D_{1}

-re. ‐ Ezzel a bizonyítást befejeztük.

Kolonits Ferenc (Budapest, Piarista g. IV. o. t.)

Megjegyzések. 1. N támaszsávjai közül a legszélesebbet, legkeskenyebbet függvényvizsgálattal is kiválaszthatjuk. Legyen

t_{1}

és

t_{3}

irányszöge

a

, erre ‐

45^{\circ} ≦ α ≦ 45^{\circ}

, metszésük

p_{1}

, ill.

p_{3}

csúcsérintőjével

T_{1}, T_{3}

A parabola érintőjének ismert tulajdonsága folytán

F_{1} T_{1}

merőleges

t_{1}

-re, így a

t_{1}, t_{3}

sáv

z

szélességét megadja

T_{1} T'_{3}

ahol

T'_{3}

T_{3}

vetülete

F_{1} T_{1}

-re. Legyen még

F_{3}

vetülete

F_{1} T_{1}

-re

F'_{3}

, ekkor

\begin{matrix} z = T_{1} T' = T_{1} F_{1} + F_{1} F'_{3} + F'_{3} T'_{3} = \\ = \frac{1}{cos α} + 4 cos α + \frac{1}{cos α} = \frac{2}{cos α} + 4 cos α, \end{matrix}

mert

F_{1} F_{3} = 4

egység.

z

tagjai pozitívok, szorzatuk állandó, így összegük akkor a legkisebb, ha egyenlők:

cos^{2} α = 1 / 2

α = \pm 45^{\circ}

, ebből

z_{min} = 4 \sqrt[]{2}

.
Másrészt

z_{max} = 6

, mert

α = 0^{\circ}

-nál éppen

z = 6

, viszont a

\begin{matrix} z - 6 = \frac{1}{cos α} (4 cos^{2} α - 6 cos α + 2) = \frac{1}{cos α} [{(2 cos α - \frac{3}{2})}^{2} - \frac{1}{4}] \end{matrix}

különbség

cos α > 0

mellett mindaddig negatív vagy

0

, amíg

\begin{matrix} - \frac{1}{2} ≦ 2 cos α - \frac{3}{2} ≦ \frac{1}{2}, 1 ≦ 2 cos α ≦ 2, - 60^{\circ} ≦ α ≦ 60^{\circ}, \end{matrix}

vagyis

α

minden vizsgált értékére.

Arató Péter (Kaposvár, Táncsics M. g. IV. o. t.)

2. Több dolgozat

2 K P_{1}

-et vette a támasznégyzet oldalának, ahol

P_{1}

t_{1}

érintési pontja.

p_{1}

-en.

K P_{1}

csak akkor merőleges

t_{1}

-re, amikor

P_{1}

C_{1}

-ben vagy

D_{1}

-ben van, különben a

t_{1}

-re

P_{1}

-ben emelt merőleges egy az

F_{1}

és

K

közötti

Q_{1}

pontban metszi az

Y

-tengelyt, mert ‐ mint a parabola említett tulajdonságából következik ‐,

Q_{1}

annak az

R_{1}

pontnak

F_{1}

-re való tükörképe, ahol

t_{1}

Y

-t metszi, erre

C_{1} R_{1}

P_{1}

ordinátájának

(- 1)

-szerese, ez pedig

D_{1}

-et kivéve kisebb

1

-nél.

^{$^{*}$}Lásd pl: KML. XVII. kötet 78. o. (1958 november).