Kezdőlap


Feladat:	981. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arató P. , Bencsik I. , Biborka T. , Bollobás B. , Bornes Klára , Csanak György , Flanek L. , Fritz J. , Hahn J. , Hajna J. , Halász G. , Hegyi L. , Holop A. , Kiss Ádám , Kolonits F. , Kovács Margit , Losonczi L. , Máté A. , Máté E. , Máté Zsolt , Mezey F. , Mihályffy L. , Muszély György , Náray M. , Parti Enikő , Pósch Margit , Raisz Klára , Sós T. , Szücs Jozsef , Tusnády G. , Várady G.
Füzet:	1960/április, 94 - 97. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Trigonometriai azonosságok, Magasságpont, Körülírt kör középpontja, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1959/május: 981. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Hogy a bizonyítandó egyenlőség bal oldalán álló szögeknek legyen értelmük, $O$ és $M$ nem eshetnek egybe. Ez csak szabályos háromszögben következnék be, emiatt a szabályos háromszöget kizárjuk. A koszinuszokat az $A O M, B O M; C O M$ háromszögekből a koszinusz tétellel kifejezve azok $K$ összege így írható:

\begin{matrix} K = \frac{(O M^{2} + r^{2} - M A^{2}) + (O M^{2} + r^{2} - M B^{2}) + (O M^{2} + r^{2} - M C^{2})}{2 O M \cdot r} = \\ = \frac{O M}{r} + \frac{O M^{2} + 3 r^{2} - (M A^{2} + M B^{2} + M C^{2})}{2 O M \cdot r}, \end{matrix}

ennélfogva elegendő megmutatni, hogy az utóbbi alak második törtjében az

S

számláló értéke 0.
Feltéve, hogy a háromszög szögeire (a szokásos jelölésekkel)

α ≦ β ≦ γ

(de nem állhat

α = γ

), legyen a

k

körülírt kör

A

-n átmenő átmérőjének másik végpontja

A^{*}

A B

felezőpontja

C_{0}

, és

C

vetülete

A B

-n

C_{1}

. Ekkor Thalész tétele alapján

A^{*} B

merőleges

A B

-re, tehát párhuzamos

C M

-mel, ugyanígy

A^{*} C

és

B M

is párhuzamosak, az

M C A^{*} B

négyszög paralelogramma, és

M C = B A^{*} = 2 C_{0} = 2 r cos B O A ∢ / 2 = 2 r cos γ

(irány szerint is, pozitívnak véve a

C_{1}

-től

C

-be mutató irányt). Hasonlóan

M A = 2 r cos α

M B = 2 r cos β

, és így

\begin{matrix} S = O M^{2} + r^{2} (3 - 4 cos^{2} α - 4 cos^{2} β - 4 cos^{2} γ) . \end{matrix}

Fejezzük ki

O M^{2}

-et az

O M C

háromszögbő1 a koszinusz-tétellel. A vele szemben fekvő szög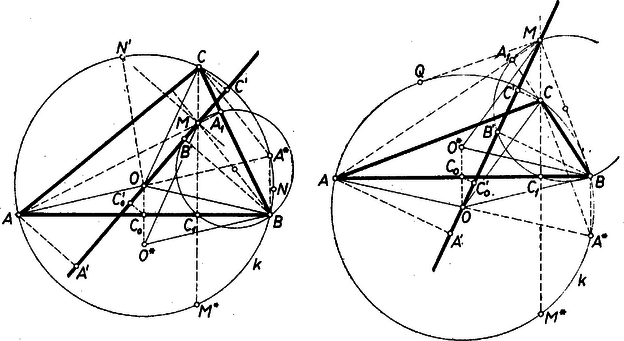

γ < 90^{\circ}

esetén

\begin{matrix} M C O ∢ = C_{1} C O ∢ = C_{1} C A ∢ - O C A ∢ = (90^{\circ} - α) - (90^{\circ} - β) = β - α, \end{matrix}

így ismert azonosságok alapján

\begin{matrix} O M^{2} & = r^{2} + M C^{2} - 2 r M C cos M C O ∢ = r^{2} [1 + 4 cos^{2} γ - 4 cos γ cos (β - α)] \\ S & = r^{2} [4 - 4 cos γ cos (β - α) - 4 cos^{2} α - 4 cos^{2} β] = \\ = 2 r^{2} [2 - cos (γ + β - α) - cos (γ - β + α) - (1 + cos 2 α) - (1 + cos 2 β)] = \\ = 2 r^{2} [2 - cos (180^{\circ} - 2 α) - cos (180^{\circ} - 2 β) - 1 - cos 2 α - 1 - cos 2 β] = 0, \end{matrix}

amit bizonyítani akartunk.

Számításunk

γ > 90^{\circ}

esetén is érvényes, mert ekkor hasonlóan

\begin{matrix} M C O ∢ = 180^{\circ} - C_{1} C O ∢ = 180^{\circ} - (β - α) . \end{matrix}

így

cos M C O ∢

helyére az előbbi kifejezés

(- 1)

-szerese lép, viszont ugyanez áll

M C

-re, mert az abszolút értékére van szükség, és ez:

∣ M C ∣ = ∣ 2 r cos γ ∣ = - 2 r cos γ

. ‐ Végül

γ = 90^{\circ}

esetén

M

C

-be esik; az

O M C

háromszög elfajul, de ekkor egyszerűbben

M \equiv C

O M = r

β = 90^{\circ} - α

, és igy közvetlenül

\begin{matrix} S = r^{2} (4 - 4 cos^{2} α - 4 sin^{2} α) = 0. \end{matrix}

Ezzel az állítást bebizonyítottuk.

Csanak György (Debrecen, Fazekas M. g. IV. o. t.)

Megjegyzés. Hogy

S = 0

, ezt trigonometriai azonosságok nélkül annak a tételnek többszöri felhasználásával is bizonyíthatjuk, hogy egy kör valamely ponton átmenő két szelője metszeteinek szorzata ugyanakkora, ‐ miután

O M^{2}

-et kifejeztük a háromszög oldalaival és a körülírt kör sugarával.
A fentiek alapján

M C^{2} = B A^{* 2} = 4 r^{2} - c^{2}

, hasonlóan

M A^{2} = 4 r^{2} - α^{2}

M B^{2} = 4 r^{2} - b^{2}

, és ezekkel

\begin{matrix} S = O M^{2} + 3 r^{2} - (12 r^{2} - a^{2} - b^{2} - c^{2}) = O M^{2} + (a^{2} + b^{2} + c^{2}) - 9 r^{2} . \end{matrix}

Legyenek

γ < 90^{\circ}

esetén az

M

-en át

O M

-re merőleges húr végpontjai

N, N'

, és

M

-nek

A B

-re vett tükörképe

M^{*}

; ismeretes, hogy ez

k

-n fekszik. Így

\begin{matrix} M N \cdot M N' = M N^{2} = M C \cdot M M^{*} = M C \cdot 2 M C_{1} = 2 M C (C_{1} C - M C) = \\ = 2 M C \cdot C_{1} C - 2 M C^{2}, \end{matrix}

folytatólag az

M B

átmérőjű Thalész-körhöz

C

-ből húzott szelők, majd az

A B C

háromszög

A B

oldalára felírt koszinusz-tétel alapján

\begin{matrix} M N^{2} = O N^{2} - O M^{2} = r^{2} - O M^{2} = 2 C A_{1} \cdot C B - 2 B A^{* 2} = \\ = (A C^{2} + B C^{2} - A B^{2}) - 2 (4 r^{2} - A B^{2}) = a^{2} + b^{2} + c^{2} - 8 r^{2}, \\ O M^{2} = 9 r^{2} - (a^{2} + b^{2} + c^{2}), \end{matrix}

és így

S = 0

. ‐ Ugyanez adódik

γ > 90^{\circ}

esetén ‐ amikor

M

k

-n. kívül van, és ezért az

M

-en átmenő második szelőként az

M Q

érintőt vesszük segítségül ‐, mert számításunkban a fentiekhez hasonlóan két előjelváltozás lép fel.

- γ = 90^{\circ}

esetén pedig

a^{2} + b^{2} + c^{2} = 2 c^{2} = 8 r^{2}

és

O M^{2} = r^{2}

, annak megfelelően, hogy

M \equiv C

Szűcs József (Szeged, Ságvári E. gyak. g. III. o. t.)

II. megoldás: Az állítás mindkét oldalát

r = O A = O B = O C

-vel szorozva vegyük észre, hogy a bal oldal tagjai az

O A, O B, O C

sugárnak az

O M

egyenesen levő vetületeit adják ‐ ha pozitívnak az

O

-ból

M

-be mutató irányt vesszük és a vetületek előjelét, is figyelembe vesszük. Legyenek a csúcsok vetületei

O M

-en rendre

A', B', C'

, ekkor azt kell megmutatnunk, hogy

\begin{matrix} O A' + O B' + O C' = O M . \end{matrix}

(1)

Ha még a fenti jelölésekkel

C_{0}

vetülete

O M

-re

C_{0}

, akkor (mindig irány szerint is tekintve)

B' C'_{0} = C'_{0} A'

, ezért

\begin{matrix} O A' = O C'_{0} + C'_{0} A', & (2) \\ O B' = O C'_{0} + C'_{0} B' = O C'_{0} - B' C'_{0} = O C'_{0} - C'_{0} A', & (3) \end{matrix}

végül az

M C C'

és

O C_{0} C'_{0}

háromszögek hasonlóságából

M C = 2 C_{0} O

folytán

M C' = 2 C'_{0} O

, és így

\begin{matrix} O C' = O M + M C' = O M + 2 C'_{0} O = O M - 2 O C'_{0} . \end{matrix}

(4)

Most már (2), (3) és (4) összegéből valóban (1) adódik.

Muszély György (Budapest, Vörösmarty M. g. III. o. t.)

Megjegyzés. Az irányított vetületeket az

O A, O B, O C

vektorok

O M

irányú összetevőinek tekintve elegendő bizonyítani, hogy a három vektor

s

összegének

O M

irányú összetevője

O M

. Ennél többet mutatunk meg: hogy

s

maga is

O M

-mel egyenlő. (Minden szakasz vektornak tekintendő). Legyen

O

tükörképe

A B

-re

O^{*}

, ekkor az I. megoldás szerint

O^{*} O = 2 C_{0} O = B A^{*} = M C

, ezért

O O^{*} M C

paralelogramma, tehát

O C = O^{*} M

. Másrészt

O A O^{*} B

egyenlő oldalú paralelogramma, és így

O A = B O^{*}

Ezekkel valóban

O A + O B + O C = B O^{*} + O B + O^{*} M = O B + B O^{*} = O^{*} M = O M

Máté Zsolt (Szeged, Radnóti M. g. III. o. t.)