Kezdőlap


Feladat:	978. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arató P. , Bartha L. , Bencsik I. , Bollobás B. , Csanak Gy. , Czékus L. , Fejes L. , Fischer A. , Flanek L. , Gáti P. , Gazsó Erzsébet , Hahn J. , Hajna J. , Halász Á. , Halász G. , Hegedűs I. , Hegedűs Katalin , Hegyi László , Holop A. , Kéry G. , Kiss Ádám , Klimó J. , Kolonits F. , Komlóssy Gy. , Kovács Margit , Losonczi L. , Máté Zs. , Mezey F. , Mihályffy L. , Molnár E. , Muszély Gy. , Náray M. , Nováky A. , Parti Enikő , Pósch Margit , Raisz Klára , Sós T. , Szűcs J. , Tihanyi A. , Tusnády G. , Várady G. , Zeke A.
Füzet:	1960/február, 55 - 56. oldal		PDF \| MathML
Témakör(ök):	Irracionális egyenletek, Paraméteres egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 1959/május: 978. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$a)$ Egyenletünk bal oldalának nincs (valós) értelme, ha bármelyik négyzetgyök jel alatt negatív szám áll. Ez akkor és csak akkor következik be, ha akár az $x - 1$ , $x - 2$ , akár az $x - 3$ , $x - 4$ tényezőpár ellentett előjelű, vagyis ha $x$ akár 1 és 2 közé, akár 3 és 4 közé esik: $1 < x < 2$ , vagy $3 < x < 4$ . ‐ Első egyenletünk második tagját a jobb oldalra áttéve, majd az egyenlet mindkét oldalát négyzetre emelve

\begin{matrix} x^{2} - 3 x + 2 = 2 - 2 \sqrt[]{2 (x - 3) (x - 4)} + x^{2} - 7 x + 12. \end{matrix}

A jobb oldalon csak a négyzetgyökös kifejezést hagyva, majd ismét négyzetre emelve és rendezve

\begin{matrix} 2 (x - 3) = - \sqrt[]{2 (x - 3) (x - 4)}, \\ 2 {(x - 3)}^{2} = (x - 3) (x - 4), \\ (x - 3) (x - 2) = 0. \end{matrix}

Innen látjuk, hogy ‐ mivel átalakításaink során gyök nem veszhetett el ‐ egyenletünket

x = 3

- on és

x = 2

-n kívül más szám nem elégítheti ki. Ezek nem kizárt értékek, és a behelyettesítés mutatja, hogy mindkettő gyöke az egyenletnek. Ezzel megkaptuk a megoldást.

b)

Második egyenletünkben hosszas vizsgálatra vezetne az a kérdés, hogy

p

r

q

, mely értékrendszerei mellett van az egyenletnek valós értelme. Ezt az

x

-et tartalmazó bal oldali tagok esetére majd a szóba jövő gyökök helyén vizsgáljuk. A jobb oldali állandó számról azonban máris feltesszük, hogy valós, vagyis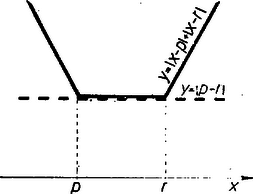

(p - r) (p - r + 2 q) \geq 0

Vegyük észre, hogy

q = 0

mellett egyenletünk

| x - p | + | x - r | = | p - r |

-re egyszerűsödik, és ennek

p \neq r

esetén minden

p

és

r

közé eső szám megoldása, beleértve

p

-t és

r

-et is (lásd az ábrát),

p = r

esetén pedig

x = p

az egyetlen gyök; másrészt, hogy

p = r

esetén a bal oldal két tagja egyenlő, és a jobb oldalon 0 áll, így a gyökök

x_{1} = p + q

x_{2} = p - q

, hacsaknem

q = 0

, amely esetet már láttunk. Feltehetjük most már, hogy

p \neq r

és

q \neq 0

.
A fentihez hasonlóan rendezés, első négyzetreemelés és átrendezés után

\begin{matrix} (p - r) (x - r + q) = \sqrt[]{(p - r) (p - r + 2 q) (x - r - q) (x - r + q)}, \end{matrix}

újabb négyzetreemeléssel és átrendezéssel

\begin{matrix} (p - r) {(x - r + q)}^{2} = (p - r + 2 q) (x - r - q) (x - r + q), \\ (x - r + q) [(p - r) (x - r + q) - (p - r + 2 q) (x - r - q)] = \\ = (x - r + q) (- 2 q x + 2 p q + 2 q^{2}) = - 2 q (x - r + q) (x - p - q) = 0. \end{matrix}

Eszerint gyökökként csak

x_{1} = r - q