Kezdőlap


Feladat:	976. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arató P. , Bartha L. , Bencsik I. , Biborka T. , Bollobás B. , Hajna J. , Halász G. , Hegedűs I. , Jahn A. , Klimó J. , Kolonits F. , Losonczi L. , Marót Ildikó , Máté Zs. , Mészáros Kornélia , Mezey F. , Molnár E. , Muszély Gy. , Nagy Ákos , Parti Enikő , Pósch Margit , S. Nagy Erzsébet , Székely J. , Szűcs J. , Tihanyi A. , Tusnády G. , Zeke A.
Füzet:	1960/február, 50 - 54. oldal		PDF \| MathML
Témakör(ök):	Elsőfokú (és arra visszavezethető) egyenletrendszerek, Számtani sorozat, Feladat
Hivatkozás(ok):	Feladatok: 1959/május: 976. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljünk minden előre beírt számot $c$ -vel, minden kiszámítandót $x$ -szel, és különböztessük meg őket úgy, hogy indexnek írjuk soruk, majd oszlopuk sorszámát; legyen továbbá az ugyanakkora összeg $S$ . Ismeretleneink száma $2 n + 1$ , $2 n$ beírandó szám (az $n$ -edik sorban $n$ , az $n$ -edik oszlopban további $n - 1$ , és $x_{11}$ ) és az összeg. Ugyanennyi a használható egyenleteink száma is, ugyanis bár a feladat $2 n + 2$ vonalon ( $n$ soron, $n$ oszlopon és $2$ átlón) írja elő az $S$ összeget, de az $n$ sor összege egyenlő az $n$ oszlop összegével, azért ez a $2 n$ egyenlet nem független egymástól, bármelyikük ‐ de csak egyikük ‐ következménye a többieknek. Valamennyi egyenletünk elsőfokú, várható tehát, hogy a felírandó rendszer megoldható, azaz ellentmondásmentes. Bizonyítási feladatunkat éppen ennek megmutatásával, a megoldás felírásával teljesítjük; innen adódik ki a válasz a további kérdésekre is.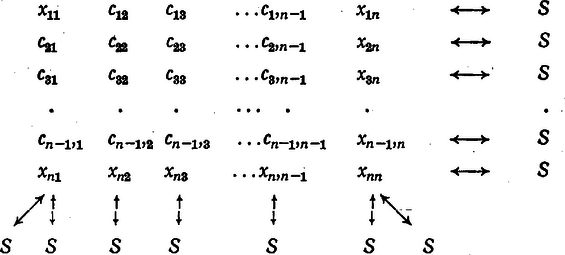

Táblázatunk alapján jól elképzelhetők az egyenletek anélkül, hogy formálisan felírnók őket. Figyeljük meg, hogy ha vesszük a sorokat az első és utolsó kivételével és a két átlót, ebben ugyanazok az ismeretlenek szerepelnek, mint az első és az utolsó oszlopban. Vegyük ezért a mondott

n - 2

sornak és a két átlónak az összegét és vonjuk ki belőle a két szélső oszlop összegét. Így egyrészt a keresett összeg

(n - 2) + 2 - 2 = n - 2

-szeresét kapjuk, másrészt valamennyi belső szám és a két átló belső számainak összegét (vagyis az átlóbeli beírt számok 2-szer veendők és páratlan

n

esetén az átlók közös száma 3-szor). Az utóbbiak mindegyike ismert szám,

n - 2 \neq 0

, mert

n - 2 \geq 1

, tehát az állandó összeg meghatározható. Legyen a belső számok összege

B

, a fő- és a mellékátló belső számainak összege

f

és

m

, így

\begin{matrix} S = \frac{B + f + m}{n - 2} . \end{matrix}

(1)

Most már az

n

-edik oszlop és az

n

-edik sor belső számai egyismeretlenes egyenletből számíthatók:

\begin{matrix} x_{i n} = S - c_{i 1} - s_{i}, x_{n i} = S - c_{1 i} - o_{i}, \end{matrix}

ahol

i = 2,3, ..., n - 1

, továbbá

o_{i}

és

s_{i}

i

-edik oszlop, ill. sor belső számainak összege. ‐ Az

n

-edik oszlop belső számainak

o_{n}

összegét az egyes számok kiszámítása nélkül az előzőkhöz hasonlóan úgy kapjuk, hogy a belső sorok összegéből ‐ ami a fentiek szerint egyenlő a belső négyzet számainak és az átlók belső számainak összegével ‐ kivonjuk a belső négyzet valamennyi számát és az első oszlop belső számainak

o_{1}

összegét. Így a kívánt összeg a két átló összege, kisebbítve az első oszlop belső számainak összegével:

\begin{matrix} o_{n} = (n - 2) S - B - o_{1} = f + m - o_{1} . \end{matrix}

(2)

Hasonlóan az

n

-edik sor belső számainak összege:

\begin{matrix} s_{n} = (n - 2) S - B - s_{1} = f + m - s_{1} . \end{matrix}

(3)

Bármelyik sarokszámra most már úgy kapunk egyismeretlenes egyenletet, ha sorának és oszlopának összegéből kivonjuk a rajta át nem menő átló összegét, pl.

x_{11}

-re, majd hasonlóan

x_{n n}, x_{1 n}, x_{n 1}

-re (1) alapján

\begin{matrix} 2 x_{11} + s_{1} + o_{1} - m = S + S - S = S, \\ x_{11} & = \frac{1}{2} (S - s_{1} - o_{1} + m) = \frac{B + f + (n - 1) m}{2 n - 4} - \frac{s_{1}}{2} - \frac{o_{1}}{2}, \\ x_{n n} & = \frac{B - (2 n - 5) f - (n - 3) m}{2 n - 4} + \frac{s_{1}}{2} + \frac{o_{1}}{2}, \\ x_{1 n} & = \frac{B + f - (n - 3) m}{2 n - 4} - \frac{s_{1}}{2} + \frac{o_{1}}{2}, \\ x_{n 1} & = \frac{B + f - (n - 3) m}{2 n - 4} + \frac{s_{1}}{2} - \frac{o_{1}}{2} . \end{matrix}

Hogy az így teljessé, vált megoldás valamennyi követelményt kielégíti, azt behelyettesítéssel könnyen ellenőrizhetjük, a legtöbb ismeretlent tartalmazó két egyenlet (

n

-edik sor,

n

-edik oszlop) esetében ezt könnyítik a (2) és (3) összegek. Ezzel bebizonyítottuk a feladat állítását, egyben látjuk, hogy a beírás csak egyféleképpen lehetséges.
(1) ‐ (3) szerint

S

csak a belső számoktól függ,

o_{n}

, és

s_{n}

pedig csak az átlóbeli belső számoktól és a szemben fekvő oldal belső számaitól. A sarokszámok mindenesetre függnek a szélső számoktól és a belső, de átlóba nem eső számoktól, ezek együtthatói ugyanis a kifejezésekben

\pm 1 / 2

, ill.

1 / (2 n - 4)

. Az átlóbeli

c_{i i}

ill.

c_{i, n + 1 - i}

számok, valamint

n = 2 k - 1

esetére a két átló közös

c_{k k}

száma a kifejezések első tagjában többször szerepel, együtthatójuk számlálóját az alábbi összeállítás mutatja:

\begin{matrix} \begin{matrix} x_{11} -ben:x_{n n} -ben:x_{1 n} -ben:x_{n 1} -ben: \\ c_{i i} i \neq n + 1 - i & 1 + 1 = 2 & 1 - (2 n - 5) = 2 (3 - n) & 2 & 2 \\ c_{i, n + 1 - i} i \neq n + 1 - i & n & 4 - n & 4 - n & 4 - n \\ c_{k k} n = 2 k - 1 & n + 1 & 3 (3 - n) & 5 - n & 5 - n \end{matrix} \end{matrix}

Eszerint

n \geq 6

esetén minden sarokszám függ minden eredetileg beírt számtól,

n = 5

esetén

x_{15}

és

x_{51}

nem függ

c_{33}

-tól.

n = 3

mellett

B

f

, és

m

egyetlen tagja

c_{22}

és

S = 3 c_{22}

, ezért a középső sor, oszlop és az átlók egymás utáni számai számtani sorozatot alkotnak; előbbi táblázatunk első két sora itt tárgytalan. A kérdés azonos az 530. gyakorlat¹

T_{1}^{*}

táblázatának előállításával.

n = 4

esetén

B = f + m

, így

S = B = c_{22} + c_{23} + c_{32} + c_{33}

, másképpen: a négy belső szám is az állandó összeget adja. Ennélfogva ugyanaz áll a négy sarokszámra is, amelyek

B

-t a két átlónak

2 S

összegére egészítik ki, valamint ugyanazért külön-külön a szélső sorok és a szélső oszlopok

2 + 2 = 4

belső számára. Előbbi táblázatunk második sora szerint a mellékátló két belső számától csak

x_{11}

függ, a mellékátló két végén álló

x_{14}

és

x_{41}

sem. Ez első hallásra meglepő, de az

S = m + f

alakból belátható, hogy vagy mindegyikük függ tőlük, vagy egyikük sem. A táblázat így alakul:

\begin{matrix} \begin{matrix} c_{23} + c_{32} + \frac{1}{2} (c_{22} + c_{33} - & c_{12} & c_{13} & \frac{1}{2} (c_{22} + c_{33} + c_{21} + c_{31} - \\ - c_{12} - c_{13} - c_{21} - c_{31}) & - c_{12} - c_{13}) \\ c_{21} & c_{22} & c_{23} & c_{32} + c_{33} - c_{21} \\ c_{31} & c_{32} & c_{33} & c_{22} + c_{23} - c_{31} \\ \frac{1}{2} (c_{22} + c_{33} + c_{12} + c_{13} - & c_{23} + c_{33} - c_{12} & c_{22} + c_{32} - c_{13} & \frac{1}{2} (c_{12} + c_{13} + c_{21} + c_{31} - \\ - c_{21} - c_{31}) & - c_{22} - c_{33}) \end{matrix} \end{matrix}

Parti Enikő (Budapest, Bagi Ilona lg. III. o. t.)

Megjegyzések. 1.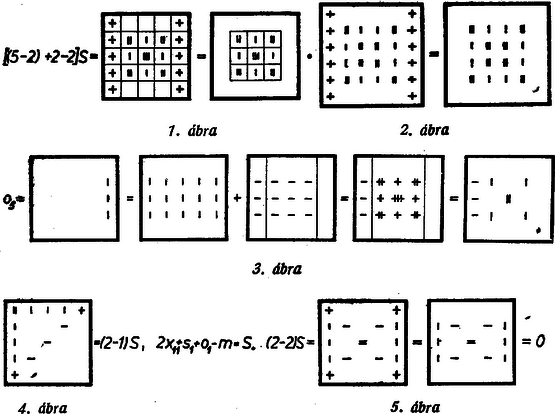

S

kiszámítására vezető meggondolásunkat

n = 5

és

n = 6

esetére úgy szemléltetjük, hogy a kifejezés tagjai helyére ,, | '', ill ,, ‐ '' jelet írunk aszerint, hogy a kérdéses tagot felvettük, ill. kivontuk. Csupa olyan tagot vontunk csak ki, amelyet előzőleg felvettünk, ezért ,, ‐ '' jel magában nem áll, csak ,, | '' jelre ráírva, ami együtt ,, + ''-nak látszik, ez azonban végeredményben a kifejezésből való hiányzást jelöli (1. és 2. ábra). Hasonlóan szemlélteti az

o_{n}

összeg meghatározását a 3. ábra,

x_{11}

-ét a 4. ábra, mindkettő

n = 5

-re.

2. A (2) és (3) összefüggésekből átalakítással és egybekapcsolással tetszetős összefüggés adódik:

\begin{matrix} o_{1} + o_{n} = f + m = s_{1} + S_{n} . \end{matrix}

Ennek első részéhez (

0

-ra redukált alakban) egyszerűbben vezet el az 5. ábrán szemléltetett elgondolás.
3.

n = 2

-vel nem volna előzetesen beírt szám, nem is létezik másodrendű ,,bűvös négyzet''.

n = 1

esetén viszont ‐ bár elfajult értelemben, ti. egytagú összegekkel ‐ van megoldás: bármely szám tekinthető elsőrendű bűvös négyzetnek.
4. Több dolgozat ,,tetszés szerinti szám''-on a hétköznapi szóhasználatot követve ‐ csak egész, sőt továbbmenve csak természetes számot értett ‐ és azt is vizsgálta, mely feltételek mellett lesznek

S

és az

x

-ek egész, ill. pozitív számok.

¹ Lásd XIX. kötet 123. o. (1959. november)