Kezdőlap


Feladat:	972. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár András
Füzet:	1960/január, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1959/április: 972. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott $A$ , $B$ pontokon átmenő körök középpontjainak mértani helye éppen a kérdéses $f$ felező merőleges, így $f$ minden ilyen körnek szimmetria-tengelye. Ezért minden egyes körnek két olyan $P_{1}$ , $P_{2}$ pontja van, amely legtávolabb van $f$ -től, ezek is $f$ -re tükrös párok, így $f$ a keresett mértani helynek is tengelye. $P_{1}$ , $P_{2}$ -t minden egyes körben az $f$ -re merőleges átmérő metszi ki.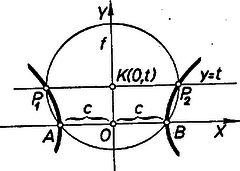

Másrészt az is nyilvánvaló, hogy a mértani helynek az

A B

egyenes is tengelye, ezért célszerű

f

-et és

A B

-t választani koordinátarendszerünk

Y

, ill.

X

-tengelyének. Legyen ennek megfelelően

A (- c, 0)

és

B (c, 0)

.
A

K (0, t)

középpont körüli

r

sugarú kör egyenlete:

x^{2} + {(y - t)}^{2} - r^{2} = 0

. Ez a kör akkor és csak akkor megy át

A

-n és

B

-n, ha

c^{2} + t^{2} - r^{2} = 0

. Eszerint a vizsgálandó körök egyenlete:

x^{2} + {(y - t)}^{2} - c^{2} - t^{2} = 0

, ahol

t

paraméter. A legtávolabbi pontokat kimetsző egyenes egyenlete

y = t

, így

P_{1}

P_{2}

abszcisszái:

x_{1,2} = \mp \sqrt[]{c^{2} + t^{2}}

, közös ordinátájuk:

y_{1,2} = t

. Ezzel megkaptuk a keresett mértani hely paraméteres egyenletrendszerét.

t

kiküszöbölésével kapjuk, hogy a mértani hely minden pontja rajta van azon a vonalon, amelynek egyenlete:

x = \mp \sqrt[]{c^{2} + y^{2}}

, másképpen

x^{2} - y^{2} = c^{2}

. Ez az az egyenlő oldalú hiperbola, amelynek a valós tengelye az

A B

szakasz.
A keresett mértani hely minden pontját akkor kapjuk meg, ha

K

-ként

f

valamennyi pontját figyelembe vesszük, más szóval ha

t

minden (valós) értéket felvesz. Eszerint a kapott hiperbola minden pontja hozzátartozik a mértani helyhez: a mértani hely ez a hiperbola.

Alpár András (Veszprém, Lovassy L. g. III. o. t.)