Kezdőlap


Feladat:	966. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bollobás Béla , Hegedüs István , Kolonits Ferenc , Komlóssy György , Tomcsányi Gyula
Füzet:	1959/december, 186 - 188. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria, Háromszögek hasonlósága, Szabályos sokszög alapú gúlák, Négyszög alapú gúlák, Középvonal, Helyvektorok, Feladat
Hivatkozás(ok):	Feladatok: 1959/március: 966. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kérdéses $S$ sík, és az $A E$ , $A B$ , $B C$ él metszéspontja rendre 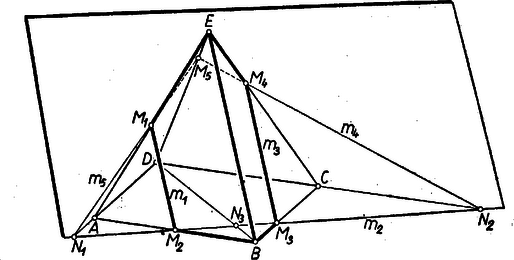$M_{1}$ , $M_{2}$ $M_{3}$ .

1. ábra

A B C D

alapsíkot

S

M_{2} M_{3} = m_{2}

egyenesben metszi, ezért

A

és

C

S

-nek a

B

-vel ellentétes oldalán van, és ugyanez áll

D

-re is, mert

D

A C

átlónak

B

-vel ellentétes oldalán van. Eszerint

S

, azaz

m_{2}

A D

C D

alapéleket (mint szakaszokat) nem metszi, de meghosszabbításaikat igen, mert metszi a velük párhuzamos

B C

, ill.

A B

egyenest, és ha két párhuzamos egyikét egy a síkjukban fekvő egyenes metszi, akkor a másikát is.

m_{2}

-nek

A D

-vel való metszéspontjára

A N_{1} = B M_{3} = B C / 3 = A D / 3

, mert az

A N_{1} M_{2}

és

B M_{3} M_{2}

háromszögek egybevágók (

A M_{2} = B M_{2}

M_{2}

-nél fekvő szögeik csúcsszögek,

A

és

B

-nél fekvő szögeik váltószögek).

m_{2}

és

C D

-nek

N_{2}

metszéspontjára pedig

C N_{2} = 2 B M_{2} = B A = C D

, mert a

C M_{3} N_{2}

és

B M_{3} M_{2}

háromszögek hasonlók (itt is két szög egyenlő és

C M_{3} : B M_{3} = 2 : 1

). Ezek szerint

N_{1}

-re

D N_{1} : N_{1} A = 4 : 1

, és

N_{2}

-re

D N_{2} : N_{2} C = 2 : 1

.
Másrészt

S

A B E

oldallap síkját

M_{1} M_{2} = m_{1}

-ben metszi, így

E

S

-nek ugyanazon oldalán van, mint

B

, vagyis ellentétes oldalán, mint

C

és

D

, eszerint

S

E C

E D

élt metszi egy

M_{4}

M_{5}

pontban, és az

E B

élt nem metszi. Pontosabban:

M_{1} M_{2}

A B E

háromszögnek a

B E

oldallal párhuzamos középvonala, tehát

S

párhuzamos

B E

-vel. Ezért

S

-nek a

B C E

síkkal való

M_{3} M_{4} = m_{3}

metszésvonala párhuzamos

B E

-vel és

E M_{4} : M_{4} C = B M_{3} : M_{3} C = 1 : 2

, vagyis

M_{4}

E C

-nek

E

-höz közelebbi harmadoló pontja. Hasonlóan

S

-nek a

B E

-n átmenő

B E D

síkkal való

M_{5} N_{3} = m_{6}

metszésvonala is párhuzamos

B E

-vel (

N_{3}

e metszésvonalnak az alapidom síkjával, más szóval

m_{2}

-nek a

B D

átlóval való metszéspontja), ezért ‐ felhasználva a

B M_{3} N_{3}

és

D N_{1} N_{3}

háromszögek hasonlóságát ‐

E M_{5} : M_{5} D = B N_{3} : N_{3} D = B M_{3} : D N_{1} = A N_{1} : D N_{1} = 1 : 4

, vagyis

M_{5}

E D

élnek

E

-höz közelebbi ötödölő pontja.
Mindezek szerint

S

a gúla 8 éle közül ötöt belső pontban metsz (a metszetidom az

M_{1} M_{2} M_{3} M_{4} M_{5}

ötszög), két élt meghosszabbításában metsz és eggyel párhuzamos.

Komlóssy György (Szolnok, Verseghy F. g. III. o. t.)

Megjegyzések: 1. Az alapidomról csak azt használtuk ki, hogy paralelogramma; nem használtuk ki az oldalélek egyenlőségét sem, így számításaink eredményei minden olyan paralelogramma alapú gúla síkmetszetére érvényesek, amelyekben az adott metszéspontok a megfelelő élt az adott arányokban osztják.
2. Hogy

B N_{3} = B D / 5

, ez abból is kiadódik, hogy egyrészt

B D

felezi az

A B C

szöget, így

M_{3} N_{3} : N_{3} M_{2} = M_{3} B : B M_{2} = 6 M_{3} B : 6 B M_{2} = 2 C B : 3 B A = 2 : 3

, tehát

M_{3} N_{3} : M_{3} M_{2} = 2 : 5

, másrészt

M_{2} N_{1} = M_{2} M_{3}

tehát

B N_{3} : B D = M_{3} N_{3} : (M_{3} N_{3} + N_{3} M_{2} + M_{2} N_{1}) = 2 : (2 + 3 + 5) = 1 : 5

. ‐ Itt kihasználtuk, hogy az alapidom rombusz.

Tomcsányi Gyula (Budapest, Toldy F. g. II. o. t.)

M_{5}

osztásarányát a Menelaosz-tétel alapján is kiszámíthatjuk, akár az

A E D

, akár a

C E D

háromszög révén.¹ Ugyanis mindkettőben ismerjük

S

-sel alkotott

m_{5}

, ill.

m_{4}

metszésvonaluk két metszéspontjának,

N_{1}

és

M_{1}

-nek, ill.

M_{4}

és

N_{2}

-nek osztóviszonyát:

(D A N_{1}) = - 4

(A E M_{1}) = 1

, ill.

(D C N_{2}) = - 2

(C E M_{4}) = 2

, és ezek felhasználásával

(D A N_{1}) (A E M_{1}) (E D M_{5}) = - 1

, ill.

(D C N_{2}) (C E M_{4}) (E D M_{5}) = - 1

bármelyikéből

(E D M_{5}) = 1 / 4

, azaz

E M_{5} : M_{5} D = 1 : 4

Kolonits Ferenc (Budapest, Piarista g. IV. o. t)

4. Kérdésünkre az ábrázoló geometria módszereivel végzett szerkesztés és erre támaszkodó számítás alapján is könnyen válaszolhatunk, mert párhuzamos vetítéssel egy egyenesen vagy párhuzamos egyeneseken fekvő egyenlő szakaszok vetületei egyenlők, ill. ilyen helyzetű szakaszok aránya nem változik meg. A 2. ábrán első képsíknak a gúla alapsíkját vettük, másodiknak pedig egy az

S

-re merőleges síkot.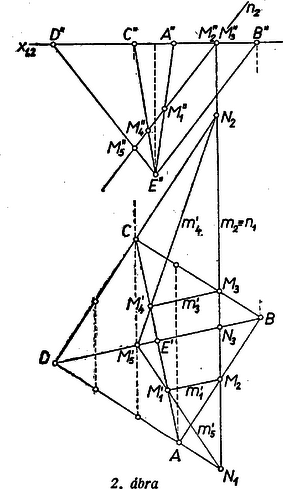

Így

S

vetítősík, a metszetidom az

n_{2}

második nyomvonalban látszik. A főleg a második képre támaszkodó számításban kihasználjuk, hogy

A'' B'' = 2 M''_{2} B'' = C'' D''

és

C'' B'' = 3 M''_{3} B'' = 3 M''_{2} B''

, tehát

A''

C''

M''_{2}

B'' D''

-t

2 + 3 = 5

egyenlő részre osztó pontok közül valók.²

Hegedűs István (Budapest, József A. g. III. o.t.)

5. Hasonlóan egyszerű a számítás alakzatunknak egy

B E

élre merőleges

T

síkon levő (derékszögű, párhuzamos vetítéssel képezett) vetületéből.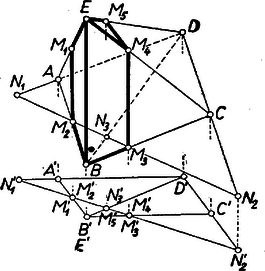

Ekkor

A' B' C' D'

paralelogramma,

E' \equiv B'

, így

M'_{1} \equiv M'_{2}

, ezért

M_{1} M_{2}

‐ és vele

S

is ‐ merőleges

T

-re, tehát a vetítési irányból nézve

S

,,élben'', az

M'_{1}

M'_{3} = m'_{2}

egyenesben látszik. Így

M'_{4}

(mint

m'_{2}

és

E' C'

metszéspontja) azonos

M'_{3}

-vel, tehát

E M_{4} : M_{4} C = E' M'_{4} : M'_{4} C' = B' M'_{3} : M'_{3} C' = B M_{3} : M_{3} C = 1 : 2

. Az

M_{5}

pont osztási aránya

M'_{5} \equiv N'_{3}

alapján a fentiekhez hasonlóan adódik.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

6. Többen térbeli koordinátageometriai úton, vagy vektorok használatával adtak választ.

¹L. pl. Kárteszi Ferenc: A Menelaos- és a Ceva-féle tétel, KML. XI. kötet, 67‐75. o. 1955. november.

²Az első képen a fentebbi megoldás $N$ -pontjai is fel vannak tüntetve; jobb térkihasználás, érdekében $E$ az első képsík alatt van.