Kezdőlap


Feladat:	965. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Arató P. , Bartha László , Biborka T. , Bollobás B. , Bürger N. , Czékus L. , Dániel Gábor , Fejes L. , Fritz J. , Hadik Z. , Hahn J. , Hajna J. , Halász Á. , Halász G. , Hegyi L. , Kiss Ádám , Kohut M. , Komlóssy Gy. , Máté A. , Máté Zs. , Mezei F. , Molnár E. , Muszély Gy. , Náray M. , Náray-Szabó G. , Parti Enikő , Pósch Margit , Sós T. , Székely J. , Szűcs J. , Tatai Péter , Tihanyi A. , Tomcsányi Gy. , Tusnády G. , Várady G. , Zeke A.
Füzet:	1960/január, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Négyzetek, Szimmetrikus alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1959/március: 965. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a $Q$ és $Q'$ négyzetek közös része a $C$ nyolcszög. $Q$ -t és $Q'$ -t közös $O$ középpontjuk körül $90^{\circ}$ -kal elforgatva mindkettő önmagába megy át, így ugyanez áll $C$ -re is.

t_{1}

egy támaszegyenese

C

-nek, akkor a belőle

O

körül egymás utáni

90^{\circ}

-os elforgatásokkal előálló

t_{2}

t_{3}

t_{4}

is támaszegyenese

C

-nek, és e négy egyenes együtt támasznégyzete a

C

-nek, mert egyrészt közülük bármelyik egymás utáni kettő derékszöget alkot, másrészt a szemben fekvő

t_{1}

t_{3}

, és

t_{2}

t_{4}

párok távolsága egyenlő

t_{1}

O

-tól való távolságának kétszeresével, és így egymással is. Eszerint

C

-nek minden támasz téglalapja négyzet,

C

négyzetekkel burkolható.

Tatai Péter (Budapest, I. István g. IV. o. t.)

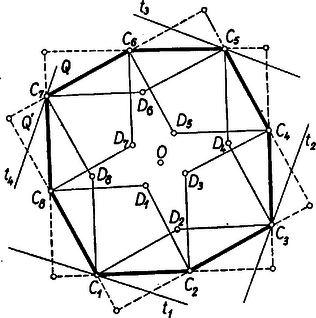
II. megoldás: Elég megmutatni, hogy

Q

és

Q'

közös

C_{1} C_{2} C_{3} C_{4} C_{5} C_{6} C_{7} C_{8} = C

része tekinthető két négyzetből képezett összegtartománynak, mert minden négyzet négyzetekkel burkolható, és két négyzetekkel burkolható alakzat összege ugyancsak négyzetekkel burkolható.¹ Valóban,

C

C_{1} C_{2}

és

C_{2} C_{3}

oldalak fölé befelé szerkesztett

Q_{1}

, ill.

Q_{2}

négyzetekből képezett összegtartomány. Legyen ugyanis a

C_{k - 1}

C_{k}

C_{k + 1}

csúcsokat paralelogrammává kiegészítő pont

D_{k}

(k = 1, 2, ..., 8

, és természetesen

C_{0} \equiv C_{8}

C_{9} \equiv C_{1}

), ekkor irány és nagyság szerint

D_{k} C_{k + 1} = C_{k - 1} C_{k} = C_{k - 2} D_{k - 1}

. Másrészt

C

fönt említett forgási szimmetriája folytán irány és nagyság szerint pl.

C_{1} C_{2} = C_{6} C_{5}

, továbbá

C_{1} C_{2}

merőlegesen áll

C_{3} C_{4}

és

C_{8} C_{7}

-re és velük egyenlő hosszú. Így

Q_{1}

és

Q_{2}

csúcsai

C_{1}

C_{2}

D_{3}

D_{8}

, ill.

C_{2}

C_{3}

D_{4}

D_{1}

. Képezzük

Q_{1}

és

Q_{2}

-nek

C'

összegét a

C_{2}

kezdőpontra vonatkozóan. Elég ebben a 4‐4 csúcsból vett

16

csúcs-pár ,,összegét'' képezni, mert

Q_{1}

Q_{2}

-vel

C'

is konvex.² Ezeket röviden táblázatunk tünteti fel, pl. a

D_{8}

sorában és

D_{4}

oszlopában álló

C_{6}

jelentése:

\vec{C_{2} D_{8}} + \vec{C_{2} D_{4}} = \vec{C_{2} C_{6}}

. Valóban

\begin{matrix} \begin{matrix} C_{2} & C_{3} & D_{4} & D_{1} \\ C_{1} & C_{1} & D_{2} & D_{5} & C_{8} & \vec{C_{2} D_{8}} + \vec{C_{2} D_{4}} = (\vec{C_{2} C_{1}} + \vec{C_{1} D_{8}}) + \\ C_{2} & C_{2} & C_{3} & D_{4} & D_{1} & + (\vec{C_{2} C_{3}} + \vec{C_{3} D_{4}}) = \\ D_{3} & D_{3} & C_{4} & C_{5} & D_{6} & = (\vec{C_{5} C_{6}} + \vec{C_{3} C_{4}}) + (\vec{C_{2} C_{3}} + \vec{C_{4} C_{5}}) = \\ D_{8} & D_{8} & D_{5} & C_{6} & C_{7} & = \vec{C_{2} C_{3}} + \vec{C_{3} C_{4}} + \vec{C_{4} C_{5}} + \vec{C_{5} C_{6}} = \vec{C_{2} C_{6}} . \end{matrix} \end{matrix}

Összegként megkaptuk valamennyi

C_{k}

és

D_{k}

pontot. Ámde mindegyik

D_{k}

belső pontja

C

-nek, mert

C

minden szöge tompaszög (a

Q

és

Q'

csúcsai körüli, lemetszett derékszögű háromszögek külső szögei), ennélfogva

\begin{matrix} D_{k} C_{k - 1} C_{k} ∢ = D_{k} C_{k + 1} C_{k} ∢ < 90^{\circ} < C_{k + 2} C_{k + 1} C_{k} ∢ = C_{k} C_{k - 1} C_{k - 2} ∢ . \end{matrix}

Eszerint

C'

csúcsai a

C_{k}

pontok és

C'

azonos

C

-vel, amit bizonyítani akartunk.

Bartha László (Balassagyarmat, Balassa B. g. IV. o. t.)

Megjegyzés. A

Q_{1} + Q_{2} = C

egyenlőséget az összegtartomány szemléletes értelmezése³ alapján is beláthatjuk. A

C_{1} C_{2}

C_{3} C_{4}

C_{5} C_{6}

C_{7} C_{8}

oldalra befelé írt négyzetek a forgási szimmetria folytán egybevágók, másrészt egyező állásúak, ezért egymásba eltolással is átvihetők:

Q_{1}

egymás utáni eltolásainak vektorai rendre

\vec{C_{2} C_{3}}

\vec{C_{4} C_{5}}

\vec{C_{6} C_{7}}

\vec{C_{8} C_{1}}

, és ezek éppen egyenlők

Q_{2}

egymás utáni oldalaival, ha ezeket vektoroknak tekintjük. Így

C

,,súrolással'' úgy is előáll, ha

Q_{1}

-et végigvezetjük

Q_{2}

kerületén (könnyű belátni, hogy ,,középen'' nem marad súrolatlan terület), vagy lefedéssel úgy, hogy a végtelen sok példányban vett

Q_{1}

-ből

C_{2}

-nél fogva

Q_{2}

-nek minden pontjára teszünk egyet.

Dániel Gábor (Budapest, Piarista g. IV. o. t.)

¹LásdKárteszi Ferenc: Négyzetekkel burkolt konvex alakzatok, KML. XVIII. köt. 1., ill. 34 o. 1959 jan., ill. febr.

²Ugyanott, 33. o.

³Ugyanott, 6. o.