Kezdőlap


Feladat:	964. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Alpár A. , Bartha L. , Biborka T. , Bódis J. , Bollobás B. , Czékus L. , Flanek L. , Fritz J. , Grallert F. , Hahn János , Halász G. , Hammer G. , Holop A. , Janositz J. , Kéry G. , Komlóssy Gy. , Losonczi L. , Máté A. , Muszély Gy. , Náray M. , Parti Enikő , Pósch Margit , Raisz Klára , Székely J. , Tusnády G. , Várady G. , Zeke A.
Füzet:	1959/december, 185 - 186. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1959/március: 964. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk a négyzet középpontját koordinátarendszerünk origójának, oldalfelezőit pedig tengelyeknek úgy, hogy a négyzet csúcsai, rendre $A (- c, - c)$ , $B (c, - c)$ , $C (c, - c)$ , $D (- c, c)$ ; legyen másrészt az $A B$ oldallal párhuzamos tetszés szerinti $e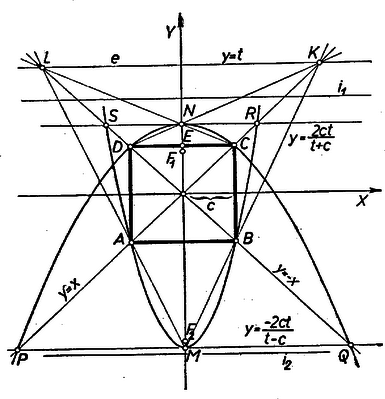$ egyenes: $y = t$ .

A C

, ill.

B D

átló egyenese

y = x

, ill.

y = - x

, így

K (t, t)

L (- t, t)

. A szimmetriákból nyilvánvaló, hogy

M

és

N

Y

-tengelyen van.

M

ordinátája a

B K

egyenes tengelymetszeteként az

y + c = (x - c) (t + c) / (t - c)

x = 0

egyenletrendszerből

y = - 2 c t / (t - c)

, eszerint

M

t = c

, azaz

K \equiv C

és

L \equiv D

eset kivételével mindig létezik.

N

ordinátáját hasonlóan kapnók

D K

-ból, egyszerűbb azonban ha

M

ordinátájában

c

helyett

- c

-t írunk:

2 c t / (t + c)

, ugyanis

D

koordinátái is így állnak elő

B

koordinátáiból;

N

t = - c

, vagyis

K \equiv A

és

L \equiv B

eset kivételével mindig létezik.
Most már

K

és

L

mintájára:

\begin{matrix} P (\frac{- 2 c t}{t - c}, - \frac{2 c t}{t - c}), Q (\frac{2 c t}{t - c}, - \frac{2 c t}{t - c}); \\ R (\frac{2 c t}{t + c}, \frac{2 c t}{t + c}), S (- \frac{2 c t}{t + c}, \frac{2 c t}{t + c}) . \end{matrix}

C

D

N

P

Q

(,,első'') pont-ötös szimmetrikus az

Y

-tengelyre, így a kérdéses parabola tengelye is csak az

Y

tengely lehet, csúcsa pedig az

N

pont. Eszerint elég azt megmutatnunk, hogy a

C

D

, ill.

P

Q

tükrös pontpárok egyik-egyik pontja kielégít egy

\begin{matrix} x^{2} = 2 p_{1} [y - 2 c t / (t + c)] \end{matrix}

alakú egyenletet, vagyis hogy a

\begin{matrix} p_{1} = \frac{x^{2}}{2 (y - \frac{2 c t}{t + c})} \end{matrix}

hányados az előjellel vett paraméterre a

C

D

pontpárral ugyanazt az értéket adja mint a

P

Q

pontpárral. Valóban, mindkét esetben

p_{1} = c (t + c) / 2 (c - t)

adódik, ‐ Hasonlóan az

A

B

M

R

S

(,,második'') pont-ötös is meghatároz egy parabolát melynek csúcsa

M

, tengelye ugyancsak az

Y

tengely, és előjeles paramétere:

\begin{matrix} p_{2} = \frac{x^{2}}{2 (y + \frac{2 c t}{t - c})} = \frac{c^{2}}{2 (- c + \frac{2 c t}{t - c})} = \frac{{(\frac{2 c t}{t + c})}^{2}}{2 (\frac{2 c t}{t + c} + \frac{2 c t}{t - c})} = \frac{c (t - c)}{2 (t + c)} . \end{matrix}

A fókusz a tengelyen a csúcstól mérve

p / 2

távolságban van, (a paraméter előjelét figyelembe véve), így paraboláink

F_{1}

, ill.

F_{2}

fókuszának abszcisszája 0, ordinátája pedig:

\begin{matrix} \frac{2 c t}{t + c} + \frac{c (t + c)}{4 (c - t)} = \frac{c (c^{2} + 10 c t - 7 t^{2})}{4 (c^{2} - t^{2})}, \\ ill. - \frac{2 c t}{t - c} + \frac{c (t - c)}{4 (t + c)} = \frac{c (c^{2} - 10 c t - 7 t^{2})}{4 (t^{2} - c^{2})} . \end{matrix}

Másrészt

C D

felezőpontja

E (0, c)

így a kérdéses egybeesés feltétele:

\begin{matrix} \frac{c (c^{2} + 10 c t - 7 t^{2})}{4 (c^{2} - t^{2})} = c, ill. \frac{c (c^{2} - 10 c t - 7 t^{2})}{4 (t^{2} c^{2})} = c \end{matrix}

amiből

\begin{matrix} t_{1} = 3 c, t_{2} = c / 3, ill. t_{3, 4} = \frac{- 5 \pm 4 \sqrt[]{5}}{11} c \approx {\begin{matrix} c \cdot 0, 3586, \\ - c \cdot 1, 268, \end{matrix} \end{matrix}

vagyis négy olyan

e

egyenes van, amelyből egy-egy

E

-fókuszú parabola adódik, kettő-kettőnél

F_{1}

, ill.

F_{2}

esik

E

-be. ‐ Az első parabolán

C

és

D

rajta fekszik, így ha

E

fókusz, akkor

| 2 p | = 2 c

. Valóban,

t_{1} = 3 c

-vel

p_{1} = - c

és

t_{2} = c / 3

-mal

p_{1} = c

adódik. Az utóbbi esetben

P \equiv C

Q \equiv D

, így az első parabola

C

, ill.

D

-ben érinti

A C

-t,

B D

-t.

Hahn János (Szeged, Déri M. gépip. t. III. o.t.)