Kezdőlap


Feladat:	963. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Arató P. , Bencsik I. , Bollobás B. , Budai Zsuzsanna , Czékus L. , Fritz J. , Gergely Antal , Hahn J. , Hajna J. , Halász Á. , Halász G. , Kéry G. , Kolonits F. , Mezei F. , Muszély Gy. , Nagy Ákos , Náray M. , Parti Enikő , Pósch Margit , Sós T. , Szücs J. , Tusnády G. , Windisch A. , Zeke András
Füzet:	1960/január, 16 - 20. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1959/március: 963. matematika feladat

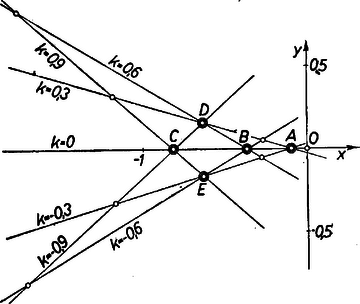
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $y = - k x - k^{3}$ alakból a $- k$ iránytényező mind a hét megrajzolt egyenesre más, tehát nincsenek köztük párhuzamosak.Így mindegyik egyenesünkön $6$ metszéspont várható, összesen pedig $7 \cdot 6 / 2 = 21$ (felezzük a $7 \cdot 6$ szorzatot, mert benne minden metszést két egyenesnél vettünk számításba). ‐ Rajzunkon viszont csak 11 különböző metszéspontot találunk, ugyanis 5 ponton 3‐3 egyenes megy át, további 6 ponton 2‐2 egyenes; az előbbieket 3-szor (pl. $a$ és $b$ , $a$ és $c$ , $b$ és $c$ metszéseként) számítva a metszések száma $3 \cdot 5 + 6 = 21$ .

A rajz szerint a

k = 0

-hoz tartozó

y = 0

egyenest, az

X

-tengelyt a

\pm 0, 3

\pm 0, 6

\pm 0, 9

k

-értékpárokhoz tartozó egyenespárok ugyanazon

A

, ill.

B

, ill.

C

pontban metszik, továbbá egy

D

ponton mennek át a

k'_{1} = 0, 3

k'_{2} = 0, 6

k'_{3} = - 0, 9

-hez tartozó egyenesek és egy

E

-n a

k''_{1} = - 0, 3

k''_{2} = - 0, 6

k''_{3} = 0, 9

-hez tartozó egyenesek. ‐ Valóban, bármely

α \neq 0

mellett a

k = α

és

k = - α

-hoz tartozó

y = - a x - a^{3}

és

y = α x + α^{3}

egyenesek egymás tükörképei az

X

-tengelyre, és így egymást e tengelyen metszik,

a - α^{2} = - {(- α)}^{2}

abszcisszájú pontban. ‐ Vegyük észre, hogy a

D

-n,

E

-n átmenő 3‐3 egyenesre

k'_{1} + k'_{2} + k'_{3} = k''_{1} + k''_{2} + k''_{3} = 0

, és ugyanez áll az előző hármasokra is:

0 + α - α = 0

. Megmutatjuk, hogy ha a tetszés szerinti, páronként egymástól különböző

k_{1}

k_{2}

k_{3}

számokra

k_{1} + k_{2} + k_{3} = 0

, akkor a megfelelő

e_{1}

e_{2}

e_{3}

egyenesek egy ponton mennek át. Így

k_{3} = - (k_{1} + k_{2})

, és egyenleteik rendre

\begin{matrix} k_{1} x + y + k_{1}^{3} = 0, & (1) \\ k_{2} x + y + k_{2}^{3} = 0, & (2) \\ - (k_{1} + k_{2}) x + y - {(k_{1} + k_{2})}^{3} = 0. \end{matrix}

(1) és (2)-ből

y

kiküszöbölése után

e_{1}

és

e_{2} M_{12}

metszéspontjának

x_{12}

abszcisszájára, majd

y_{12}

ordinátájára:

\begin{matrix} {\begin{matrix} x_{12} = - \frac{k_{1}^{3} - k_{2}^{3}}{k_{1} - k_{2}} = - k_{1}^{2} - k_{1} k_{2} - k_{2}^{2} = - {(k_{1} + k_{2})}^{2} + k_{1} k_{2}, \\ y_{12} = - k_{1} x_{12} - k_{1}^{3} = k_{1}^{2} k_{2} + k_{1} k_{2}^{2} = k_{1} k_{2} (k_{1} + k_{2}), & (3) \end{matrix} \end{matrix}

és ezek kielégítik a harmadik egyenletet, tehát a harmadik egyenes valóban átmegy az első kettő metszéspontján. Ezzel a rajzunk alapján sejtett szabályszerűséget bebizonyítottuk.
Több

k

-hoz tartozó egyenes berajzolása esetén nem jön létre olyan metszéspont, amelyen háromnál több egyenes megy át. Ennek bizonyítása végett megmutatjuk előbbi eredményünk fordítottját: ha (rajzunkon csak

k x + y + k^{3} = 0

egyenesek vannak megrajzolva és) valamely

M

ponton három

e_{1}

e_{2}

e_{3}

, egyenes megy át: (1), (2) és a

k_{3}^{3}

-hoz tartozó

\begin{matrix} k_{3} x + y + k_{3}^{3} = 0, \end{matrix}

(4)

akkor

k_{1} + k_{2} + k_{3} = 0

. Valóban, feltevésünk azt jelenti, hogy

M

-ben

M_{12}

, és az

e_{1}

és

e_{3}

-nak a (3) mintájára adódó

M_{13} (- k_{1}^{2} - k_{1} k_{3} - k_{3}^{2},

k_{3}^{2} k_{3} + k_{1} k_{3}^{2})

metszéspontja egybeesnek:

\begin{matrix} - k_{1}^{2} - k_{1} k_{2} - k_{2}^{2} = - k_{1}^{2} - k_{1} k_{3} - k_{3}^{2} \end{matrix}

és

\begin{matrix} k_{1}^{2} k_{2} + k_{1} k_{2}^{2} = k_{1}^{2} k_{3} + k_{1} k_{3}^{2} . \end{matrix}

E két egyenlőséget

0

-ra redukálva

\begin{matrix} - k_{1} (k_{2} - k_{3}) - (k_{2} - k_{3}) (k_{2} + k_{3}) = (k_{3} - k_{2}) (k_{1} + k_{2} + k_{3}) = 0 \end{matrix}

és

\begin{matrix} k_{1}^{2} (k_{2} - k_{3}) + k_{1} (k_{2}^{2} - k_{3}^{3}) = k_{1} (k_{2} - k_{3}) (k_{1} + k_{2} + k_{3}) = 0. \end{matrix}

k_{2} \neq k_{3}

, folytán az elsőből

k_{1} + k_{2} + k_{3} = 0

ez a másodikból is adódik, ugyanis az indexek alkalmas választásával

k_{1} \neq 0

.
Ha már most

M

-en a

k_{4}

-hez tartozó

e_{4}

is átmenne, akkor

e_{1}

e_{2}

és

e_{4}

közös pontja folytán

k_{1} + k_{2} + k_{4} = 0

; és így

k_{4} = k_{3}

tehát

e_{4}

nem különböző

e_{3}

-tól.
Mindezek alapján (rajz nélkül) kimondhatjuk, hogy a

21

egyenes esetében annyiszor

2

metszéspont esik egybe egy korábbival, ahányféleképpen az adott

21

számból választott három különböző szám összegeként

0

-t kapunk. Ha

k_{1} = 0

, akkor ez

k_{2} = α

és

k_{3} = - α

-val

10

-féleképpen lehetséges. Ha mindhárom

k

különbözik

0

-tól, akkor kettő egyenlő jelű, a harmadik ezek összegének ellentettje. Egyszerűség kedvéért az értékek

10

-szeresével dolgozva azt kell keresnünk, hányféleképpen lehet előállítani az

1, 2, ..., 10

számokat két különböző természetes szám összegeként. Ez rendre

0

0

1

1

2

2

3

3

4

4

-féleképpen, összesen 20-féleképpen lehetséges. (Általában

2 k - 1

és

2 k

-ra egyaránt

k - 1

előállítás van:

2 k - 1 = 1 + (2 k - 2) = 2 + (2 k - 3) = ... = (k - 1) + k

és

2 k = 1 + (2 k - 1) = 2 + (2 k - 2) = ... = (k - 1) + (k + 1)

. Ezt a számot

(- 1, - 2, ..., - 10

-es összegek !) kétszer véve rajzunkon

10 + 2 \cdot 20 = 50

háromszoros metszés pont lenne, továbbá

21 \cdot 10 - 3 \cdot 50 = 60

egyszeres, összesen

110

Zeke András (Budapest, Bolyai J. g. III. o. t.)

Megjegyzések. 1. A feladat

7

egyenesre vonatkozó részével azt céloztuk, hogy megoldóink ,,kísérleti úton'', kicsiben, olyan keretek között, amelyet még kis munkával lehet megrajzolni, észrevegyék a szabályszerűségeket. Ennyi tapasztalatszerzés és annak helyes megmagyarázása elegendő alap ahhoz, hogy a

21

egyenes bonyolultabb esetét már elméleti úton oldhassuk meg. Sokan azonban pontatlan vázlatból, vagy rajz nélkül indultak, a valóságot torzítva, vagy vele mit sem törődve; ,,róla-nélküle'' írtak a kérdésről. Ne tápláljunk olyan téves nézeteket, hogy egyes esetek vizsgálata nem illő a matematikushoz. Ellenkezőleg, igen sok vizsgálat ‐ az új kérdések kezdeti vizsgálata igen gyakran ‐ egyes esetekből indul ki. A matematika elvonással általános tételeket állapít meg, de a semmiből nem lehet absztrahálni.
2. Tekintsük a

k^{3} + x k + y = 0

egyenletben

k

-t ismeretlennek,

x

y

-t együtthatóknak, így egy ún. redukált harmadfokú egyenlet áll előttünk (a köbös tag együtthatója

1

, a négyzetesé

0

). Gondoljuk másrészt minden valós

k

számhoz megrajzolva az ezen egyenlettel jellemzett egyenest. Így minden egyes

k_{0}

-hoz tartozó egyenes a rajta fekvő

(x, y)

pontok koordináta párjai révén megadja az összes olyan redukált harmadfokú egyenletek

(x, y)

együttható párját (

x

mindig az elsőfokú tag együtthatója,

y

az ismeretlentől mentes tag), amelyeknek a

k_{0}

szám gyöke; és fordítva: minden egyes

(x_{0}

y_{0})

együttható párral meghatározott

(x_{0}, y_{0})

ponton átmegy minden olyan valós

k

-hoz tartozó egyenes, amely kielégíti az ezen együtthatókkal felírt redukált harmadfokú egyenletet. Eszerint ‐ tudva azt, hogy minden valós együtthatós harmadfokú egyenletnek vagy egy valós gyöke van, vagy három ‐ az utóbbi esetben közülük kettő vagy három meg is egyezhet ‐, kapjuk, hogy a sík minden pontján vagy egy egyenes megy át vagy három, esetleg kivételesen kettő.
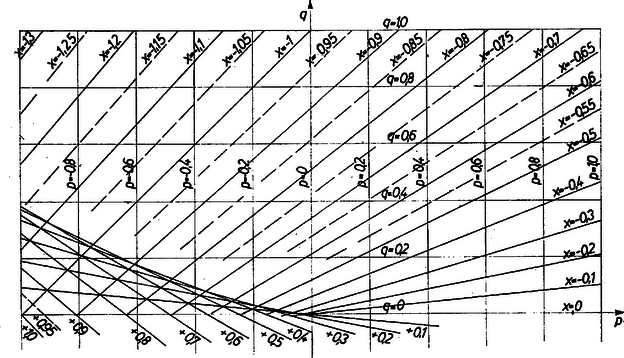
Ha már most az áttekinthetőség érdekében a berajzolt egyenesek számát megfelelően csökkentjük, akkor (természetesen bízva abban, hogy pl. a kihagyott

k = 0, 537

-hez tartozó egyenes valahol a

k = 0, 5

-höz és a

k = 0, 6

-hoz tartozó egyenesek között vagy a közelükben halad) rajzunkról a redukált harmadfokú egyenletek valós gyökét (gyökeit) közelítőleg leolvashatjuk. Ábránk a redukált harmadfokú egyenlet valós gyökeinek közelítő leolvasására szolgáló vonalsereges (egyenessereges) nomogram. ^{$^{*}$} A redukált harmadfokú egyenletet az

x^{3} + p x + q =

= 0

általános alakban szokás írni, ezért ábránk tengelyeit is

p

q

-val jelöltük, az eddigi

k

helyére pedig

x

lép.

Pl. az

x^{3} - 0, 73 + 0, 072 = 0

egyenlet gyökei a rajz szerint, amennyire a

(- 0, 73;