Kezdőlap


Feladat:	957. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arató Péter , Bollobás Béla , Czékus Laborc , Czinege I. , Dániel G. , Fejes L. , Grallert F. , Hadik Z. , Hajna J. , Halász G. , Jahn A. , Kisvölcsey J. , Klimó J. , Kolonits F. , Máté A. , Máté Zs. , Mezei F. , Molnár E. , Muszély Gy. , Náray M. , Parti Enikő , Pósch Margit , S. Nagy Erzsébet , Sellei Á. , Szücs J. , Tatai P. , Tusnády G. , Várady G.
Füzet:	1959/december, 180 - 184. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Pont körüli forgatás, Feladat
Hivatkozás(ok):	Feladatok: 1959/február: 957. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás (csak a szerkesztés) Feladatunknak az 1958. évi Arany Dániel verseny haladó csoport II. fordulóján kitűzött 3. feladat¹ speciális esete, ott $φ = 60^{\circ}$ . Másrészt $φ = 30^{\circ}$ esetén az $A B C$ háromszöghöz megszerkesztett $A_{1}$ , $B_{1}$ , $C_{1}$ , pontokkal az $A C_{1} B A_{1} C B_{1}$ hatszögre teljesülnek az 1956. évi Arany Dániel verseny haladó csoport II. fordulója 3. feladatának² feltételei (2 ‐ 2 szomszédos oldal egyenlő, az egyenlő szomszédos oldalak közti szögek $120^{\circ}$ -osak), így az ott bebizonyított tétel szerint az $A_{1} B_{1} C_{1}$ háromszög szabályos; ezért adott $A_{1}$ , $B_{1}$ , $C_{1}$ -ből vagy egyáltalán nem szerkeszthető $A B C$ , vagy számtalan sok szerkeszthető. A $φ = 30^{\circ}$ esetet ezért kizárjuk.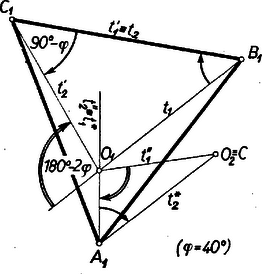
Az 1958. évi versenyfeladatra közölt II. megoldás gondolatmenetét átvéve megoldást kapunk, ha az ottani forgatások szögét, ill. a tükörtengelyek közti szöget az alábbiak szerint módosítjuk.

C

csúcsnak

B_{1}

, majd

C_{1}

végül

A_{1}

(

C

-t

A

-ba, majd

B

-be, végül

C

-be vivő) forgatásai

180^{\circ} - 2 φ

szöggel végzendők az

A_{1} B_{1} C_{1} = H_{1}

háromszög körüljárásával ellentétes irányban (mert ott az 1. (és 5.) ábrán

A B C = H

és

H_{1}

körüljárása pozitív,

C A B_{1}

A B C_{1}

B C A_{1}

,-é viszont negatív); minden további forgás is így értendő. Ezért az 5. ábra

t_{1}

-et

t_{2}

-be,

t'_{1}

-et

t'_{2}

-be és

t_{1}^{*}

-et

t_{2}^{*}

-be vivő forgásainak szöge

90^{\circ} - φ

, a

t_{1}

-et

t'_{2}

-be és

t''_{1}

-et

t''_{2}

-be vivő,

O_{1}

körüli forgások szöge

180^{\circ} - 2 φ

, végül a

t''_{1}

-et

t_{2}^{*}

-be vivő forgási

ε = 270^{\circ} - 3 φ

. Az

O_{2}

körüli

ε

forgással ismét csak

O_{2}

, kerül eredeti helyére (ott marad), tehát

C \equiv O_{2}

.
Mivel

0^{\circ} < φ < 90^{\circ}

, azért

O_{1}

mindig létezik; ugyanígy

O_{2}

is, hacsaknem

t''_{1}

és

t_{2}^{*}

párhuzamosak vagy egybeesők. Ez csak akkor állhatna be, ha

180^{\circ} - 2 φ

és

90^{\circ} - φ

kiegészítő szögek (a kizárt

φ = 30^{\circ}

esete), ill.

φ = 90^{\circ}

mellett, amikor a föléirt háromszögek értelmüket vesztik. Így

A B C

megszerkesztése mindig egyértelműen elvégezhető, tehát ha van, akkor egy megoldás van.

Czékus Laborc (Budapest, Toldy F. g. III. o. t.)

Megjegyzések. 1.

O_{1} A_{1}

B C

szakasz felező merőlegese, mert az idézett megoldás szerint

B

és

C

O_{1}

és

A_{1}

pontok mindegyike körüli forgással egymásba vihetők át, tehát egyenlő távolságra vannak

O_{1}

-től és

A_{1}

-től. Így

O_{1} A_{1}

C B A_{1}

háromszög tengelye, megszerkeszthetők a hozzá

90^{\circ} - φ

szöggel hajló

A_{1} B

és

A_{1} C

száregyenesek, és közülük az veendő

A_{1} C

-nek, amelyet a

H_{1}

körüljárásával egyező irányú,

180^{\circ} - 2 φ

szögű forgás visz át a másikba. Így kaphatjuk

B_{1} C

B_{1} A

C_{1} A

C_{1} B

-t is, és a megfelelő metszéspontok adják

H

csúcsait.
2. Megkaphatjuk

H

-t hasonlósági transzformációval is abból, hogy

B C

iránya merőleges

O_{1} A_{1}

-re, és ugyanígy

C A

A B

irányát megszerkesztve akárhány a

H

-hoz hasonló helyzetű

H^{*}

háromszöget kaphatunk. Egy ilyenhez megszerkesztve a megfelelő

A_{1}^{*}

B_{1}^{*}

C_{1}^{*}

csúcsokat, a nyert

H_{1}^{*}

háromszög nyilván ugyancsak hasonló helyzetű

H_{1}

-hez.

H_{1}^{*}

és

H_{1}

-nek

S

hasonlósági pontjából mint középpontból

H^{*}

megfelelő nyújtásával kapjuk

H

-t.
3. A szerkesztés a fentiek szerint akkor is elvégezhető, ha a kívánt egyenlő szárú háromszögek alapján fekvő

φ

ψ

ω

szögeknek egymástól különbözőknek kell lenniük.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

II. megoldás: Szerkesszük meg a pozitív körüljárású

A B C = H

háromszöghöz a

C_{1}

A_{1}

B_{1}

pontokat (a

H_{1}

háromszöget) és forgassuk el egyrészt a

B_{1} A C_{1}

, háromszöget

B_{1}

körül, másrészt az

A_{1} B C_{1}

háromszöget

A_{1}

körül úgy, hogy

A

, ill.

B

csúcsuk

C

-be jus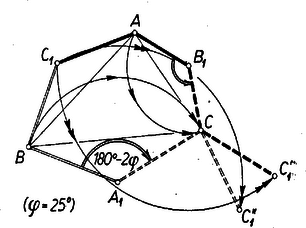son.

A forgások szöge

ω = 180^{\circ} - 2 φ

, az oldalak fölé írt háromszögek új csúcsánál fekvő szög. Legyen

C_{1}

új helyzete

C'_{1}

, ill.

C''_{1}

. Ekkor a

C C'_{1} C''_{1} = H'

háromszög egyenlő szárú, mert

C C'_{1} = A C_{1} = B C_{1} = C C''_{1}

.
Meghatározzuk a

H'

alapján fekvő szögeket és azt, hogy

C

C'_{1} C''_{1}

egyenes melyik partján fekszik. Első forgatásunk pozitív, a második negatív irányú, mert az

A C_{1} B A_{1} C B_{1}

hatszög és vele

H_{1}

is pozitív körüljárású (húzzunk vezérsugarat

H

bármely belső pontjából

H

, ill. a hatszög kerületét bejáró ponthoz). Így a

C C'_{1} = f_{1}

félegyenest

C

körül

C C''_{1} = f_{2}

-be átvivő pozitív forgás szöge:

ϑ = C'_{1} C B_{1} ∢ + B_{1} C A_{1} ∢ + A_{1} C C''_{1} ∢ = C_{1} A B_{1} ∢ + B_{1} C A_{1} ∢ + A_{1} B C_{1} ∢ = (α + 2 φ) + (γ + 2 φ) + (β + 2 φ) = 180^{\circ} + 6 φ

. Így

ϑ

nagyobb

180^{\circ}

-nál, ezért

H'

szárai rövidebb forgással is átvihetők egymásba; a következőkben megmutatjuk

C

szerkesztését

ϑ

különböző értékei mellett.
Ha

φ < 30^{\circ}

, akkor

ϑ < 360^{\circ}

, így

f_{2}

-t

f_{1}

-be

360^{\circ} - ϑ = 180^{\circ} - 6 φ (< 180^{\circ})

, szögű pozitív forgás viszi át, ezért

H'

csúcsainak

C''_{1}

C'_{1}

C

sorrendje ad pozitív körüljárást, benne

C''_{1} ∢ = C'_{1} ∢ = 3 φ (< 90^{\circ})

. Így

C

szerkesztése:

C_{1}

-nek

B_{1}

körüli

+ (180^{\circ} - 2 φ)

és

A_{1}

körüli

- (180^{\circ} - 2 φ)

szögű forgatásával előáll

C'_{1}

és

C''_{1}

, ezek felező merőlegeséből

C

-t az a

C''_{1} C

száregyenes metszi ki, amely a

C''_{1} C'_{1}

félegyenesből

+ 3 φ

szögü forgással áll elő.

A

-t és

B

-t hasonlóan kaphatjuk, de pl.

A

-t megadja a

C B_{1}

-ből

+ φ

és

B_{1} C

-ből ‐(

180^{\circ} - 2 φ

) forgatással előálló félegyenesek metszéspontja is.
(

φ = 30^{\circ}

mellett

ϑ = 360^{\circ}

, így

C''_{1} \equiv C'_{1}

; ez is felhívná a figyelmet ennek az esetnek külön vizsgálatára.)

30^{\circ} < φ < 60^{\circ}

mellett

360^{\circ} < ϑ < 540^{\circ}

, így

f_{1}

-et

C

körül

f_{2}

-be átviszi a

(0^{\circ} <) ϑ - 360^{\circ} = 6 φ - 180^{\circ} (< 180^{\circ})

szögű forgás,

H'

-nek a

C'_{1} C''_{1} C

körüljárása pozitív, az alapon fekvő szögek nagysága

[180^{\circ} - (6 φ - 180^{\circ})] / 2 = 180^{\circ} - 3 φ) (< 90^{\circ}

φ = 60^{\circ}

mellett (a versenyfeladat esete)

ω = 60^{\circ}

és

ϑ = 540^{\circ} = 360^{\circ} + 180^{\circ}

, így

H'

egyenes szakasszá fajul,

C

felezőpontja

C'_{1} C''_{1}

-nek.³

60^{\circ} < φ < 90^{\circ}

mellett

540^{\circ} < ϑ < 720^{\circ}

f_{1}

átjut

f_{2}

-be a

(0^{\circ} <) 720^{\circ} - ϑ = 540^{\circ} - 6 φ (< 180^{\circ})

forgással is,

H'

körüljárása ismét a

C''_{1}

C'_{1}

C

sorrendben pozitív, az alapon

[180^{\circ} - (540^{\circ} - 6 φ] / 2 = 3 φ - 180^{\circ} (< 90^{\circ})

nagyságú szögek vannak.
A fentiek alapján

φ

minden figyelembe veendő értéke mellett megszerkeszthetjük

C

-t.
A speciális

φ = 45^{\circ}

esetben

2 ω = 180^{\circ}

, ez a különleges érték módot nyújt egyszerűsítésre, pl.

C''_{1}

mellőzhető.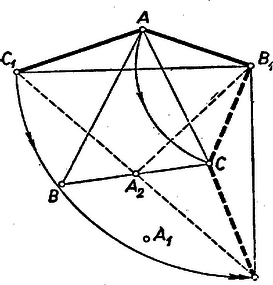

Így ugyanis

C_{1} B

és

C C'_{1}

C_{1} A

-hoz képest

- 90^{\circ}

, ill.

+ 90^{\circ}

-kal vannak elfordulva, tehát párhuzamosak. Ezért a

C_{1} B C'_{1} C

négyszög paralelogramma, ismert

C_{1} C'_{1}

átlójának

A_{2}

felezőpontja megadja az ismeretlen

B C

átló (azaz oldal) felezőpontját. Sőt

C'_{1}

-t is mellőzhetjük, mert ez esetben

C_{1} C'_{1} B_{1}

egyenlő szárú derékszögű háromszög (átfogója

C_{1} C'_{1})

, ezért ugyanez áll

B_{1} C_{1} A_{2}

-re is (átfogója

B_{1} C_{1}

), tehát

A_{2}

-t az adott

B_{1} C_{1}

oldal fölé befelé írt egyenlő szárú derékszögű háromszög harmadik csúcsaként egyszerűbben kapjuk. Ugyanígy szerkesztjük

C A

és

A B

-nek

B_{2}

C_{2}

felezőpontját, ezekből pedig

H

-t. (A háromszögek befelé szerkesztendők, ugyanis a

B_{1} C_{1}

,-et

B_{1} A_{2}

-be vivő forgás pozitív, mert fele a

C'_{1}

-t előállító forgásnak, és arról láttuk, hogy pozitív ‐ akárcsak a

B_{1} C_{1}

-ből

B_{1} A_{1}

-be vivő forgás.)
A fentiek szerint az

A_{2} B_{2} C_{2} = H_{2}

háromszög középháromszöge

H

-nak, tehát hasonló helyzetűek, akárcsak a

φ = 60^{\circ}

esetben (csak a nagyítási arány más). Itt is van olyan felvétel (pl. ha

H_{1}

szögei:

30^{\circ}

60^{\circ}

90^{\circ}

, amelyben

A_{1}

B_{1}

C_{1}

a kész

H

-hoz képest nem a kifelé, hanem a befelé írt megfelelő háromszögek csúcsainak bizonyulnak, és ilyenkor is

H_{2}

és

H

H_{1}

-gyel ellentétes körüljárásúak. Ebből az idézett cikk gondolatmenetét mindenben követve annak feltételéül, hogy

H_{2}

H_{1}

-gyel azonos körüljárásúnak adódjék, ezt kapjuk:

\begin{matrix} 4 sin α sin β sin γ > sin^{2} α + sin^{2} β + sin^{2} γ \end{matrix}

(a mintabeli

\sqrt[]{3}

számok helyén mindenütt 1 áll). Ezt az említett példa

(30^{\circ}

60^{\circ}

90^{\circ})

nem teljesíti:

\sqrt[]{3}

nem nagyobb, mint 2.

Arató Péter (Kaposvár, Táncsics M. g. IV. o. t.)

Megjegyzés.

φ = 45^{\circ}

esetén

H

csúcsait forgatások nélkül úgy is megkapjuk, ha

H_{1}

mindegyik magasságára a csúcstól a szemben fekvő oldal felé felmérjük a szemben fekvő oldalt, pl.

A_{1}

-ből a

B_{1} C_{1}

felé, rá merőlegesen felmért

B_{1} C_{1}

szakasz végpontja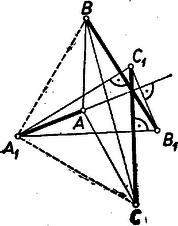

A

Valóban, így pl. az

A_{1} B_{1} B

és

C C_{1} A_{1}

háromszögek egybevágók, hiszen

A_{1} B_{1} = C C_{1}

B_{1} B = C_{1} A_{1}

és

A_{1} B_{1} B ∢ = C C_{1} A_{1} ∢

, mert merőleges szárú hegyes szögek (a magasságszakasz a megfelelő oldalszakaszokkal hegyes szöget zár be). A két oldalpár merőlegessége folytán a

B A_{1}

és

A_{1} C

harmadik oldalak is merőlegesek, másrészt az egybevágóság folytán egyenlők, így

A_{1}

valóban a

B C

átfogó fölé valamelyik oldalra szerkesztett egyenlő szárú derékszögű háromszög harmadik csúcsa.

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

III. megoldás: Forgassuk el a

B_{1} C_{1} A

háromszöget

B_{1}

körül

+ 2 φ

szöggel, amennyi a

C_{1} B A

háromszög

C_{1}

-nél fekvő külső szöge; így az

A C_{1}

oldal új

A^{*} C_{1}^{*}

helyzete párhuzamos és egyirányú

C_{1} B

-vel. Ezért

C_{1} B C_{1}^{*} A^{*}

paralelogramma, tehát az ismert

C_{1} C_{1}^{*}

átló

F

felezőpontja a

B A^{*}

átlót is felezi.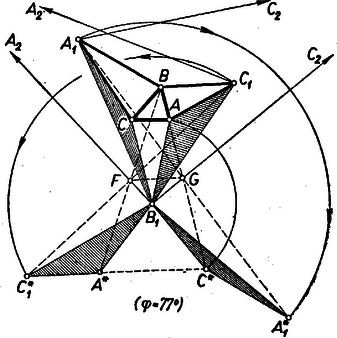

Hasonlóan kapjuk a

B_{1} A_{1} C

háromszögnek

B_{1}

körül.

- 2 φ

szöggel

B_{1} A_{1}^{*} C^{*}

-ba való elforgatása és az

A_{1} B A_{1}^{*} C^{*}

paralelogramma révén

B C^{*}

-nak

G

felezőpontját.

F G

párhuzamos

A^{*} C^{*}

-gal, mert a

B A^{*} C^{*}

háromszög középvonala, tehát

C A

-val is, mert az

A C A^{*} C^{*}

négyszög egy a

B_{1}

középpontú,

B_{1} A

sugarú körbe írt szimmetrikus trapéz. Eszerint

F G

megadja

C A

irányát. Hasonlóan kapjuk

A B

B C

irányát is, és belőlük az 1. megoldás 2. megjegyzésében leírt módon a keresett

H

-t.

φ = 45^{\circ}

esetén ez a szerkesztés is egyszerűsödik:

A^{*} \equiv C

és

C^{*} \equiv A

-ra, és tovább

F \equiv A_{2}

G \equiv C_{2}

-re vezet; a II. megoldás szerkesztésével való azonosságot az magyarázza, hogy itt

2 φ = ω

. (L. P.)

Megjegyzések. 1. Láttuk, hogy

H_{1}

oldalai fölé befelé

φ = 60^{\circ}

és

φ = 45^{\circ}

alapszögű egyenlő szárú háromszögeket szerkesztve a harmadik csúcsok által alkotott

H_{2}

háromszög hasonló helyzetű az eredeti

H

-hoz, és így vele azonos körüljárású. Megmutatjuk, hogy ez a tény bármely

φ \neq 30^{\circ}

hegyes szög esetén fennáll. Ehhez elég belátnunk

H

és

H_{2}

, egy tetszés szerinti megfelelő oldalpárjának párhuzamosságát. ‐ Valóban,

F

B_{1} C_{1} C_{1}^{*}

egyenlő szárú háromszög

C_{1} C_{1}^{*}

alapjának felezőpontja, a

B_{1}

-nél levő szög

2 φ

, ezért

F B_{1} C_{1} ∢ = φ

, tehát

A_{2}

B_{1} F

egyenesen fekszik, továbbá

F

B_{1} C_{1} A_{2}

háromszög

B_{1} A_{2}

szárához tartozó magasság talppontja. (Így lesz

B_{1} C_{1} A_{2}

befelé írt háromszög, mert

C_{1}^{*}

F

és

A_{2}

ugyanazon oldalán van

B_{1} C_{1}

-nek, mint

A_{1}

.) Ugyanígy

C_{2}

B_{1} G

egyenesen van és

G

A_{1} B_{1} C_{2}

, háromszög

B_{1} C_{2}

oldalához tartozó magasság talppontja. Mivel pedig a

B_{1} C_{1} A_{2}

és

A_{1} B_{1} C_{2}

háromszögek hasonlók, azért

B_{1} A_{2} : B_{1} C_{2} = B_{1} F : B_{1} G

, ennélfogva

A_{2} C_{2}

párhuzamos

F G

-vel és a fentebbiek szerint

A C

-vel, amit bizonyítani akartunk.

H_{2}

ezen tulajdonsága alapján tetszőleges

φ

-re elvégezhetjük az idézett cikknek megfelelő diszkussziót, alább ezt vázoljuk.

\sqrt[]{3}

helyett

tg φ = μ

-vel a feladat követelményét kielégítő

H

háromszög létezésének feltétele:

\begin{matrix} (3 μ^{2} + 1) sin α sin β sin γ > μ (sin^{2} α + sin^{2} β + sin^{2} γ) . \end{matrix}

(1)

Ezen egyenlőtlenség fennállásának szükséges feltétele, hogy

H_{1}

szögei a

\begin{matrix} \frac{3 μ^{2} + 1}{2} sin α - μ - μ (1 - cos α) = 0 \end{matrix}

egyenlet gyökei által meghatározott ,,középső'' intervallumba essenek. Innen (egyszersmind

ctg φ = 1 / μ = ν

-vel is kifejezve

\begin{matrix} cos α = \frac{8 μ^{2} \pm (9 μ^{4} - 1)}{9 μ^{4} + 10 μ^{2} + 1}, \\ cos α_{1} = \frac{9 μ^{4} + 8 μ^{2} - 1}{9 μ^{4} + 10 μ^{2} + 1} = \frac{(9 μ^{2} - 1) (μ^{2} + 1)}{(9 μ^{2} + 1) (μ^{2} + 1)} = \frac{9 μ^{2} - 1}{9 μ^{2} + 1} = \frac{9 - ν^{2}}{9 + ν^{2}}, \\ cos α_{2} = \frac{- 9 μ^{4} + 8 μ^{2} + 1}{(9 μ^{2} + 1) (μ^{2} + 1)} = \frac{1 - μ^{2}}{1 + μ^{2}} = \frac{ν^{2} - 1}{ν^{2} + 1} . \end{matrix}

0^{\circ}

-hoz ,,közel járó''

φ

-vel

(μ \approx 0) α_{2}

,,közel jár''

0^{\circ}

-hoz, mert

cos α_{2} \approx 1

α_{1}

pedig

180^{\circ}

-hoz, mert

cos α_{1} \approx - 1

; és hasonlóan

90^{\circ}

-ot megközelítő

φ

-vel

(ν \approx 0) α_{1} \approx 0^{\circ}

és

α_{2} \approx 180^{\circ}

, vagyis a ,,középső'' intervallum a

H_{1}

szögeire majdnem minden értéket megenged. Ha viszont a diszkrimináns:

9 μ^{4} - 1 = 0

, azaz

μ = 1 / \sqrt[]{3}

φ = 30^{\circ}

, akkor az intervallum egyetlen pontra zsugorodik össze:

cos α_{1} = cos α_{2} = 1 / 2

α_{1} = α_{2} = 60^{\circ}

, ennél ‐ mint tudjuk ‐

H_{1}

szögei sem kisebbek, sem nagyobbak nem lehetnek. Mennél távolabb van

φ

a ,,kritikus''

30^{\circ}

értéktől (akár felette, akár alatta), annál tágabb határok között változtatható az adott

H_{1}

alakja.

φ = 45^{\circ}

-ra a határok

cos α_{1} = 4 / 5

-ből

α_{1} \approx 36, 9^{\circ}

és

cos α_{2} = 0

-ból,

α_{2} = 90^{\circ}

.
Végül

α

-val

H_{1}

legkisebb szögét jelölve (1) fennállásinak elégséges feltételeként (a cikk jelöléseivel) az

\begin{matrix} f {(α, β - γ)}_{β - γ - 180^{\circ} - 3 α} = 2 sin^{2} α [(3 μ^{2} + 1) sin α cos α - μ (sin^{2} α + 3 cos^{2} α)] > 0 \end{matrix}

egyenlőtlenségre jutunk. A bal oldal 0-helyei:

tg α_{1} = 3 μ

és

tg α_{2} = 1 / μ

. Ezekből

φ = 30^{\circ}

esetén

α_{1} = α_{2} = 60^{\circ}

, minden más esetben

α_{1}

és

α_{2}

egyike kisebb

60^{\circ}

-nál: Ha

α

(vagyis

H_{1}

mindegyik szöge) nagyobb ennél, akkor

H

megszerkeszthető.

Lőrincz Pál

2. A

cos 2 φ = (1 - {tg}^{2} φ) / (1 + {tg}^{2} φ) = (1 - μ^{2}) / (1 + μ^{2})

azonosság alapján látjuk, hogy a közbülső intervallum egyik határa

α_{2} = 2 φ

. Hasonlóan

3 tg φ = 3 μ = tg ψ

jelöléssel

- cos α_{1} = cos (180^{\circ} - α_{1}) = (1 - {tg}^{2} ψ) / (1 + {tg}^{2} ψ) = cos 2 ψ

-ből

α_{1} / 2

annak a szögnek a pótszöge, amelynek tangense 3-szorosa

φ

tangensének. A szükséges feltételt adó ezen eredményekhez az 575. gyakorlat⁴ általánosításában egyszerűbben jutottunk el; ott azonban kizárólag egyenlő szárú

H_{1}

háromszögekről és elfajult

H_{2}

-ről volt szó. Innen viszont (ti. az idézett cikk vizsgálataiból) a kérdésünkre megoldást adó bármely

H_{1}

-ről többet tudtunk meg.

¹Lásd a megoldást KML. XVII. kötet 76‐79. o. és Lőrincz Pál hozzáfűzött megjegyzéseit 128‐134. o. (1958. november, ill. december)

²Lásd a megoldást KML. XIII. kötet 78. o. 1956. november.

³A versenyfeladat 1. ábráján $A_{2}$ , $B_{2}$ , megfelel $C'_{1}$ , $C''_{1}$ -nek, mert pl. a $C_{1}$ körüli $- 60^{\circ}$ -os forgással $B_{1}$ ugyanoda jut, mint $B_{1}$ , a $C_{1}$ körüli $+ 60^{\circ}$ -os forgással.

⁴Lásd ezen számban, 176. o.