Kezdőlap


Feladat:	952. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Durst István , Hammer Géza
Füzet:	1959/november, 104 - 105. oldal		PDF \| MathML
Témakör(ök):	Legnagyobb közös osztó, Feladat
Hivatkozás(ok):	Feladatok: 1959/február: 952. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tekintsük az $a$ , $b$ , $c$ , $d$ számoknak törzsszámhatványok szorzatára bontott alakját, és képezzük ezekből a szükséges legnagyobb közös osztókat (tovább röviden LKO) is szorzat-alakban. Ebben minden $p$ törzsszámnak a kitevője egyenlő azoknak a kitevőknek a legkisebbikével, amelyekkel $p$ a megfelelő számok felbontott alakjában szerepel. Így a bizonyítás minden egyes $p$ -re külön végezhető annak megmutatásával, hogy $p$ a bizonyítandó egyenlőség két oldalán ugyanazon kitevővel szerepel. Legyen $p$ kitevője $a$ , $b$ , $c$ , $d$ felbontásában rendre $α$ , $β$ , $γ$ , $δ$ , így az $a b$ és $c d$ szorzatokban $α + β$ , ill. $γ + δ$ és $a b = c d$ folytán $α + β = γ + δ$ . A kitevők nagyságviszonya $2^{3} = 8$ -féle lehet.

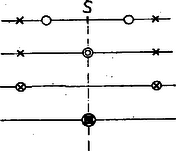
A kapott összefüggés ugyanis szemléletesen azt jelenti, hogy egyrészt

α

és

β

-nak, másrészt

γ

és

δ

-nak a számvonalon levő képei egymásnak ugyanazon

S

pontra, a számtani közepüket ábrázoló pontra tükörképei, tehát e két pontpár egyike ,,külső'', másika ,,belső'' pontpár (az ábrán

\times

, ill.

◯

jellel; természetesen lehetségesek egybeesések, lásd az ábra változatait). Eszerint

2

lehetőség van arra, hogy a két kitevőpárnak melyike a külső, és további

2

‐

2

lehetőség arra, hogy a pároknak melyik tagja a kisebb.

γ

és

δ

nagyságviszonyát azonban figyelmen kívül hagyhatjuk, mert

c

és

d

felcserélésével a bizonyítandó egyenlőség önmagába megy át, így feltehetjük, hogy

γ \leq δ

. A maradó

4

nagysági sorrend mellett

p

-nek

(a, c)

-ben,

(a, d)

-ben és

(a

b

c

d)

-ben adódó

κ

λ

, ill.

μ

kitevőjét, végül a bizonyítandó egyenlőség bal oldatán adódó

κ + λ - μ

kitevőjét az alábbi táblázat tünteti fel. Az utolsó sor mutatja, hogy e kitevő egyenlő a jobb oldalon álló

a

-beli kitevővel, tehát az állítás helyes.

\begin{matrix} α \leq γ \leq δ \leq β & β \leq γ \leq δ \leq α & γ \leq α \leq β \leq δ & γ \leq β \leq γ \leq δ \\ κ & α & γ & γ & γ \\ λ & α & δ & α & α \\ μ & α & β & γ & γ \\ κ + λ - μ & α & (γ + δ) - β = & α & α \\ = (α + β) - β = α \end{matrix}

Durst István (Szolnok, Verseghy F. g. III. o. t.)

II. megoldás: Felhasználunk két a LKO-ra vonatkozó egyenlőséget:^{$^{*}$}

\begin{matrix} ((l, m, ...), (l', m', ...)) = (l, m, ...; l', m', ...), \end{matrix}

(1)

‐ vagyis két LKO-nak LKO-ja egyenlő valamennyi szóban forgó szám LKO-jával ‐

\begin{matrix} k (l, m, ...) = (k l, k m, ...), \end{matrix}

(2)

‐ vagyis adott számok LKO-jának

k

-szorosa egyenlő a

k

-szor akkora számok LKO-jával, és fordítva: az adott számok bármely közös tényezője a LKO jeléből kiemelhető. Így

(a, c)

-t átmenetileg

e

-vel is jelölve az idézett egyenlőségek, valamint a

c d = a b

feltevés alapján

\begin{matrix} (a, c) \cdot (a, d) & = e (a, d) = (a e, d e) = (a (a, c), d (a, c)) = ((a^{2}, a c), (a d, c d)) = \\ = (a^{2}, a c, a d, c d) = (a^{2}, a c, a d, a b) = a (a, b, c, d) . \end{matrix}

A bizonyítandó egyenlőség innen osztással adódik. Az osztásnak nincs akadálya, mert

(a, b, c, d) \geq 1

Hammer Géza (Budapest, Toldy F. g. III. o. t.)

^{$^{*}$}Lásd: Kürschák‐Hajós‐ Neukomm‐Surányi: Mat. Versenytételek I. 103. o. Tankönyvkiadó, 1955)