Feladat: 951. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bollobás Béla ,  Csanak György ,  Máté Zsolt ,  Németh László 
Füzet: 1959/december, 178 - 180. oldal  PDF  |  MathML 
Témakör(ök): Szabályos testek, Feladat
Hivatkozás(ok):Feladatok: 1959/január: 951. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Minden olyan síklapokkal határolt konvex test szabályos dodekaéder, amelyet 12 egybevágó szabályos ötszög határol (1), és minden csúcsában 3 ilyen lap találkozik (2). Azt kell tehát megmutatnunk, hogy a D testnek megvan e két tulajdonsága.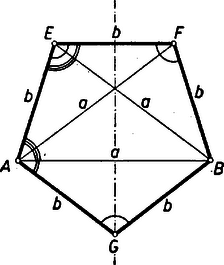
A P testek K-hoz nem tartozó csúcsaiban 3 lap találkozik. Ugyanez áll D-nek K-val közös csúcsaira, mert minden ilyen csúcsban három P találkozik, mindegyiken két kívülről látható lap van, és ez a 3⋅2 lap-rész kettesével egy-egy lapot alkot. Eszerint D-nek megvan a (2) tulajdonsága.

 
 

Az (1) tulajdonsághoz elég megmutatni, hogy D egy lapja szabályos ötszög. Legyen az ABCD kockalapra illesztett P-nek további két csúcsát összekötő él párhuzamos AB-vel, végpontjai legyenek E, F, és az ABRS kockalapra illesztett P-nek A, B-vel, háromszöget alkotó csúcsa G. Az AGBFE lapon a feltevés folytán AG=GB=BF=FE=EA=b; megmutatjuk, hogy szögei is egyenlők. Láttuk, hogy AF=BE=AB=a, ennélfogva az AEF, EFB, BGA egyenlő szárú háromszögek egybevágók, tehát az E, F, G csúcsnál fekvő szögek egyenlők. A tengelyes szimmetria folytán A és B-nél is egyenlő szögek feküsznek, elég tehát belátni az A és E-nél fekvő szögek egyenlőségét. Ezeket az AB, EB átlók 2 ‐ 2 egyenlő részre osztják, mert az említett egybevágóság folytán a GAB és FEB, másrészt a BAE és BEA szögek egyenlők, ugyanis az AEB háromszög egyenlő szárú. ‐ Ezzel a bizonyítást befejeztük.
 

Máté Zsolt (Szeged, Radnóti M. g. III. o. t.)
 

II. megoldás: Az (1) tulajdonság fennállását az alábbiak szerint is beláthatjuk: A hivatkozott megoldás szerint az AGBFE ötszög b oldalai és AB=AF=BE=a átlói között fennáll az ab+b2=a2 összefüggés. Innen a(a-b)=b2, tehát egyrészt a>b, másrészt a:b=b:(a-b). Ez azt jelenti, hogy ha az AB szakaszon úgy tűzzük ki H-t, hogy BH=BG=b, ennélfogva AH=a-b, akkor az ABG és AGH háromszögekben AB:AG=AG⋅AH, és mivel bennük az ezen oldalak közti szög közös, azért hasonlók. Így AGH is egyenlő szárú háromszög, tehát BAG∢=α jelöléssel BGH∢=BHG∢=2α, és a BGH háromszög szögeinek összegéből α=180∘:5=36∘, továbbá BGA∢=108∘. Ugyanekkora szög fekszik E és F-nél, így az ötszög A és B-nél fekvő, a szimmetria folytán egyenlő szögeinek összege 540∘-3⋅108∘=216∘, tehát ezek is 108∘-osak, az ötszög szabályos.
 

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.)
 

Megjegyzés. Az ab+b2=a2 összefüggés alapján a szögeket trigonometriai úton is megkaphatjuk. b-nek a hivatkozott megoldáshoz fűzött 1. megjegyzésben közölt kifejezésével cosα=a/2b=(5+1)/4, ebből pedig α=36∘.2
 

Németh László (Sopron, Széchenyi I. g. IV. o. t.)

 

III. megoldás: Bebizonyítjuk, hogy D köré lehet gömböt írni. Ebből következik, hogy a lapok körbe írhatók, mert a körülírt gömbnek a lapsíkokkal való metszete kör, a körbeírt egyenlő oldalú sokszög pedig szabályos.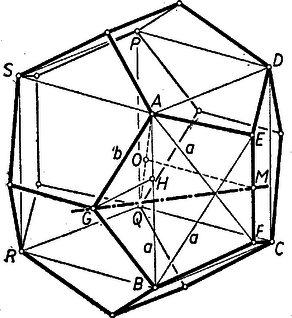
 
 

Az említett G gömb K-nak is körülírt gömbje, így középpontja csak az AQ átló O felezőpontjában lehet, és sugara r=AQ/2=a3/2. Már most EF felező pontját M-mel jelölve a hivatkozott megoldás (1) kifejezése és az a(a-b)=b2 összefüggés alapján: OM=a2+m=a2+a(a-b)2=a+b2, másrészt ME=b/2, tehát
OE2=OM2+ME2=a2+(2ab+2b2)4=a2+2a24=r2,
vagyis E, F és a nekik megfelelő további pontok valóban G-n vannak.
 

Csanak György (Debrecen, Fazekas M. gyak. g. IV. o. t.)

2Lásd pl. Faragó László: Mat. szakköri feladatgyűjtemény (2. kiad.) 194. o. (Tankönyv-kiadó, 1955).