Kezdőlap


Feladat:	950. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Czinege Imre , Raisz Klára , Serfőző Gusztáv , Székely Jenő , Tihanyi Ambrus , Valkó János
Füzet:	1959/november, 103 - 104. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Rombuszok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1959/január: 950. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tegyük fel, hogy a kérdéses tulajdonságú $A D$ ív létezik, pontjainak sorrendje az íven: $A$ , $B$ , $C$ , $D$ , tehát $\hat{A B} = \hat{B C} = \hat{C D}$ , és jelöljük az $O B$ , $O C$ egyenesnek $A D$ -vel való metszéspontját $B_{1}$ , $C_{1}$ -gyel, tehát $A C_{1} = C_{1} B_{1} = B_{1} D$ . Ennélfogva $A D$ felező merőlegese $C_{1} B_{1}$ -et is felezi, a $C_{1} B_{1} O$ háromszög egyenlő szárú. Legyen továbbá $O C$ -nek a körrel való második metszéspontja (a rövidebb $A D$ íven) $E$ . Ekkor a $C_{1} A E$ és $C_{1} B_{1} O$ háromszögek egybevágók, mert $C_{1} A = C_{1} B_{1}$ , $C_{1}$ -nél fekvő szögeik csúcsszögek, $C_{1} E A ∢ = C E A ∢ = C O A ∢ / 2 = C O B ∢ = C_{1} O B_{1} ∢$ , ennélfogva $A E = B_{1} O = C_{1} O = C_{1} E = r / 2$ .
Eszerint a körön tetszés szerint felvett $A$ ponthoz létezik $D$ , és ezt azzal az $A C_{1}$ egyenessel metszhetjük ki, amely felezi az $A E = r / 2$ hosszúságú húr $E$ végpontjához tartozó $O E$ sugarat. $E$ és vele $C_{1}$ egyértelműen van meghatározva.

Serfőző Gusztáv (Budapest, Madách I. g. IV. o. t.)

Megjegyzés: Az eddigiekből

O B_{1} # A E

is következik, ennélfogva

B_{1}

paralelogrammává egészíti ki az

O A E

háromszöget, tehát az

A D

egyenes

A

-ból és

B_{1}

-ből is meghatározható. ‐ Másképpen: az

A

-n átmenő átmérő másik végpontját

F

-fel jelölve

O C_{1}

középvonala az

F B_{1} A

háromszögnek, így

F B_{1} = 2 O C_{1} = r

, tehát

B_{1}

F

körül

r

és

O

körül

r / 2

sugárral írt körök metszéspontjaként is szerkeszthető.

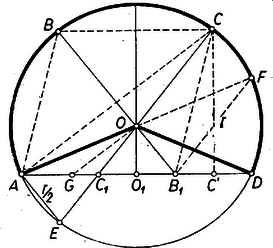Tihanyi Ambrus (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

II. megoldás:

O B

felezi az

O A

és

O C

egyenesek szögét, így

O B_{1}

külső szögfelezője az

O A C_{1}

háromszögnek, ezért

O C_{1} : O A = B_{1} C_{1} : B_{1} A = 1 : 2

.
Most már, az

O

-ból induló belső szögfelező talppontját

G

-vel jelölve

G C_{1} : G A = O C_{1} : O A = 1 : 2

, így

G

harmadolja

A C_{1}

-et, ennélfogva

A B_{1}

-et is. Ennek alapján a tetszés szerint felvett

A D

húrhoz megszerkeszthetjük azt a kört, amelyben a kívánt tulajdonság fennáll: megszerkesztjük

A D

-n

B_{1}

-et, majd

G

-t, és (a két szögfelező merőlegessége alapján) a

G B_{1}

átmérő fölé írt Thalész-körrel

A D

felező merőlegeséből kimetsszük

O

-t.

Czinege Imre (Pannonhalma, Bencés g. IV. o. t.)

III. megoldás: Az

A B C B_{1}

négyszög deltoid, mert az

O B \equiv B_{1} B

átló felező merőlegese az

A C

átlónak. Másrészt

B

és

D

A C

egyenesnek ellentétes partjain vannak, és a kerületi szögek tétele folytán

B C A ∢ = D A C ∢

, így

B C ∥ A D = A B_{1}

, és a deltoid szimmetriája folytán

B A ∥ C B_{1}

. Eszerint az

A B C B_{1}

négyszög rombusz:

B C = A B_{1} = 2 A D / 3

.
Mindebből az is következik, hogy az

A B C D

négyszög szimmetrikus trapéz,

C

-nek az

A D

-n levő

C'

vetülete felezi

B_{1} D

-t, továbbá, hogy

C D = B C = 2 A D / 3

.
Ezzel újabb módot nyertünk

A D

-hez a kör megszerkesztésére:

A D

-t

6

egyenlő részre osztva az

A

-tól

4

-ik osztópont

B_{1}

, az ötödik

C'

, a

C'

-ben emelt merőlegest

D

-ből

D C = A B_{1}

sugárral elmetszve megkapjuk

C

-t.

Székely Jenő (Pécs, Nagy Lajos g. II. o. t.)

IV. megoldás: Az I. megoldás

E O A

szöge kiegészítő szöge a három egyenlő részre osztott

A O D

szög kétharmadának,

A O C

-nek. Így

A O D ∢ = 6 α

jelöléssel

E O A ∢ = 180^{\circ} - 4 α

, és az

E O A

egyenlő szárú háromszögből

sin E O A / 2 = sin (90^{\circ} - 2 α) = cos 2 α = A E / 2 A O = 1 / 4

. Innen

2 α \approx 75^{\circ} 31, 3'

és

6 α = 226^{\circ} 34'

Valkó János (Budapest, Rákóczi F. g. IV. o. t.)

Megjegyzések: 1. A III. megoldás

C D C'

derékszögű háromszögében

C D C' ∢ = C D A ∢ = C O A ∢ / 2 = 2 α

, és így

cos 2 α = C' D / C D = 1 / 4

.
2.

A D

felezőpontját

O_{1}

-gyel és

O O_{1}

-et

d

-vel jelölve az

O O_{1} B_{1}

és

O O_{1} D

derékszögű háromszögekből

O_{1} B_{1} = d