Feladat: 943. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Arató P. ,  Bollobás B. ,  Czékus L. ,  Dániel G. ,  Fritz J. ,  Gaál Sándor ,  Gyene András ,  Hajna J. ,  Halász G. ,  Kelemen József ,  Kisvölcsey J. ,  Kolonits F. ,  Máté A. ,  Mayer G. ,  Mezei F. ,  Mihályffy L. ,  Náray Miklós (Bp.) ,  Papp Éva ,  Simonfai L. ,  Szász D. ,  Szatmári G. ,  Szücs J. ,  Tusnády G. 
Füzet: 1959/október, 53 - 55. oldal  PDF  |  MathML 
Témakör(ök): Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1958/december: 943. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Élérintő gömb létezéséhez elegendő a tetraéderre vonatkozó feltevéseknek már az a része is, hogy egy lap szabályos ‐ más szóval 3 nem szemköztes él egyenlő ‐, valamint hogy a további 3 ‐ egy csúcsba összefutó, és így ugyancsak nem szemköztes ‐ él ugyancsak egyenlő. Így ugyanis teljesül a 879. feladatban bebizonyított elegendő feltétel:1 mindhárom szemköztes él‐pár összege ugyanakkora, hiszen az (u oldalú) ABC szabályos háromszöget alapnak véve az ezzel szemközt fekvő D csúcsban összefutó (v hosszúságú) élek oldalélek, és minden szemköztes él‐párt egy alapél és egy oldalél alkot, így mindhárom összeg értéke u+v. Másrészt a kiemelt rész‐feltevésekből az ortocentrikusság is következik. Ugyanis az előbbi v‐élek egyenlősége folytán D-nek az ABC síkra való D' vetületére D'A=D'B=D'C, tehát D' azonos az ABC háromszög O középpontjával; így pedig D'A≡OA⊥BC, ennélfogva DA⊥BC, és ugyanez áll a többi szemköztes él‐párra.
A feltétel szükséges voltának bizonyításához tegyük fel, hogy az ABCD ortocentrikus tetraédernek ‐ melynek szemben fekvő él‐párjai AB=c és CD=f, BC=a és AD=d, CA=b, és BD=e ‐ van élérintű gömbje. Így teljesül az élérintő gömb létezésének szükséges feltétele:2

a+d=b+e=c+f=állandó=p.(1)
Másrészt az ortocentrikusság feltevéséből a 887. feladatban bebizonyított tétel szerint3
a2+d2=b2+e2=c2+f2=állandó=r.(2)
Most már (1) négyzetéből (2)-t levonva, majd 2-vel osztva
ad=be=cf=12(p2-r)=q.(3)
(1) és (3) egybevetéséből látjuk, hogy az a, d, a b, e és a c, f számpárok mindegyike ugyanazon másodfokú egyenletnek, x2-px+q=0-nak gyök‐párjával egyenlő. Eszerint tetraéderünkön legfeljebb kétféle élhosszúság fordulhat elő, mindegyik 3-szor, és szemközti élek csak akkor egyenlők, ha mind a 6 él egyenlő. (Létező tetraéderből indultunk ki, így a gyökök biztosan valósak.)
Legyenek az egyenlet gyökei, a két élhossz: u és v, és tekintsük a tetraéder egy v hosszúságú v1 élét. Ehhez a végpontjain minden más él csatlakozik ‐ kivéve a vele szemben fekvő u hosszúságú u1 élt ‐, mindegyik végponton 2 él. A két további v-él : v2 és v3 a v1-nek vagy ugyanazon végpontjához kapcsolódik, vagy két különbözőhöz. Az előbbi esetben megtaláltuk a tetraéder egyenlőélű csúcsát, legyen ez D, a v-élek ,,szabad'' végpontjai pedig A, B, C. Így a DA, DB, DC éllel szemben fekvő BC, CA, AB élek hossza u, tehát az ABC háromszög szabályos. ‐ Ha pedig v2 és v3 a v1-nek két különböző végpontjához, A' és B'-höz kapcsolódik pl. A'-hoz v2 és ennek szabad végpontja C', akkor a B'-ből kiinduló B'D' él hossza u, mert szemben fekszik A'C'-vel, így a B'-ből kiinduló v3 él másik végpontja ugyancsak C'. Eszerint az A'B'C' háromszög minden oldala, éle v, a szemben fekvő u-élek pedig D-ben futnak össze. ‐ Ezzel bebizonyítottuk a kimondott feltétel szükséges voltát.
 

Gyene András (Budapest, Eötvös J. g. IV. o. t.)
 

Megjegyzés: A fentivel lényegében azonos megoldásra jutunk, ha a tetraédernek az ortocentrikussággal ekvivalens azon tulajdonságából indulunk ki, hogy éltengelyei (a szemközti élek felezőpontjait összekötő F1F2, F3F4, F5F6 szakaszok) egyenlők,1 ami azt is jelenti, hogy az F1F3F2F4, F1F5F2F6 és F3F5F4F6 paralelogrammák derékszögűek.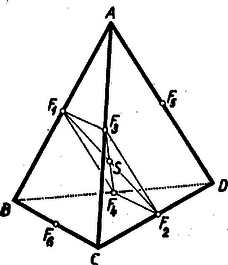
 
 
1. ábra
 

E téglalapok az átlókon felül a kerület mértékszámában is megegyeznek, mert (1) alapján pl. az elsőnek a kerülete: F1F3+F3F2+F2F4+F4F1=(F1F3+F2F4)+(F3F2+F4F1)=BC+AD=a+d=p. Így pedig egybevágók, mert egyszerű számítás mutatja, hogy az átló és a kerület a téglalap oldalait egyértelműen meghatározza. Eszerint a lapok F1F3, F1F4, ..., F4F6 középvonalai között csak kétféle hosszúság fordulhat elő, ennélfogva a 2-szer akkora élek között is, amit fentebb tisztán számítással mutattunk meg.
 

Gaál Sándor (Veszprém, Lovassy L. g. IV. o. t.)
 

II. megoldás: A feltétel szükséges voltát a csúcsokból az él‐érintő gömbhöz húzható érintőszakaszok (él‐részek) vizsgálatával is bebizonyíthatjuk.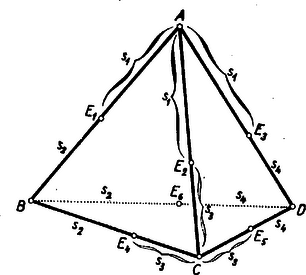
 
 
2. ábra
 

Az éleket ezekkel kifejezve a=s2+s3, d=s1+s4, b=s1+s3, e=s2+s4, c=s1+s2, f=s3+s4 és az ortocentrikusság feltétele így alakul:
(s2+s3)2+(s1+s-4)2=(s1+s3)2+(s2+s4)2=(s1+s2)2+(s3+s4)2.
és innen
s2s3+s1s4=s1s3+s2s4=s1s2+s3s4.
Az első egyenlőségből átrendezéssel (s1-s2)(s4-s3)=0, vagyis az s1=s2 és s3=s4 egyenlőségek közül legalább az egyik teljesül. Hasonlóan a második egyenlőségből vagy s1=s4, vagy s2=s3, vagy mindkettő fennáll.
Ha pl. s1=s2 és s1=s4, akkor az ABD háromszög szabályos, mert mindegyik oldala 2s1, és a C-be befutó 3 él is egyenlő: mindegyiknek s1+s3 a hossza. Bárhogy kapcsolunk össze az előbbi 2‐2 egyenlőségből 1‐1-et, mind a 3 további ilyen esetben hasonló eredményre jutunk. Ezzel a bizonyítást befejeztük.
 

Kelemen József (Szentgotthárd, Vörösmarty M. g. IV. o. t.)

1Lásd KML. XVII. kötet, 99-101. o. (1958. november).

2Lásd KML. XVI. kötet, 5. o. (1958. január).

3Lásd KML. XVII. kötet,112‐114. o. (1958. november).

1Lásd KML. XVI. kötet 35. o. (1958. február).