Kezdőlap


Feladat:	942. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arató Péter , Bollobás B. , Csanak Gy. , Czékus L. , Dániel G. , Elekes B. , Endrődy T. , Fritz J. , Gazsó Erzsébet , Gyene A. , Kéry G. , Kolonits F. , Máté A. , Máté E. , Máté Zs. , Mocskónyi M. , Náray Miklós (Bp.) , Papp Éva , Sillay B. , Szász Domokos , Szatmári G. , Székely J. , Tihanyi A. , Tomcsányi Gy. , Trón L. , Tusnády G.
Füzet:	1959/november, 95 - 97. oldal		PDF \| MathML
Témakör(ök):	Irracionális számok és tulajdonságaik, Háromszögek nevezetes tételei, Síkgeometriai számítások trigonometriával, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1958/december: 942. matematika feladat

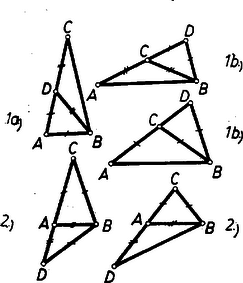
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feladat szövege a $D$ pontnak $A C$ -n való kitűzését kétféleképpen teszi lehetővé: $A$ -tól vagy $C$ oldalán, vagy $A C$ -nek $A$ -n túl való meghosszabbításán. Aszerint is két lehetőséggel kell számolnunk $D$ helyzetére, hogy az első esetben az $A B C$ egyenlő szárú háromszög alapja kisebb, vagy nagyobb a száránál. Végül első hallásra a $B C D$ háromszög egyenlő szárú voltát is háromféleképpen képzelhetjük el, ugyanis bármelyik két oldalának egyenlőségére gondolhatunk. Mindenesetre $D ≢ C$ , különben $B C D$ elfajult háromszög lenne, tehát $A B = A D \neq A C$ , $A C B ∢ \neq 60^{\circ}$ . E kérdéseknek minden lehető módon való megválasztása után esetről esetre kiszámíthatjuk az $A B C$ háromszög szögeit (ugyanis az $A B D$ és $B C D$ háromszögek egyenlő szárú voltából további egyenletet kapunk a két ismeretlen szögére), és ennek alapján adunk választ a kérdésre.

1. a) Legyen

A D

egyirányú

A C

-vel és

A B < A C

; így

D

A C

szakaszra esik. Ekkor

B A C ∢ > 60^{\circ}

B D C ∢ = 90^{\circ} + B A D ∢ / 2 > 120^{\circ}

, tompa szög, így a

B D C

háromszög csak úgy lehet egyenlő szárú, ha

D B = D C

. Ekkor,

B A C ∢ = A B C ∢ = α

és

A C B ∢ = γ

jelölésekkel mindenképpen

2 α + γ = 180^{\circ}

, továbbá feladatunkban

B D C ∢ = 90^{\circ} + α / 2 = 180^{\circ} - 2 γ

, és ebből

α = 540^{\circ} / 7

γ = 180^{\circ} / 7

. Így az

A B C

háromszög, vagy ami ugyanaz, a

γ

szög megszerkesztése egyértelmű a szabályos

14

-szög szerkesztésével, erről pedig tudjuk, hogy euklidészi értelemben nem szerkeszthető meg.
1. b) Legyen

A D

egyirányú

A C

-vel és

A B > A C

, tehát

D

A C

-nek

C

-n túli meghosszabbításán van.

B C D

-ben nem lehet

C B = C D

, mert ez a feltevés

A B = A D = A C + C D = A C + C B

-re vezet, és így az

A B C

háromszög nem létezik. Így két lehetőség marad

B C D

egyenlő szárúságára:

D B = D C

-ből

A D B ∢ = 90^{\circ} - α / 2

révén

D C B ∢ = 90^{\circ} - A D B ∢ / 2 = 45^{\circ} + α / 4 = C A B ∢ + C B A ∢ = 2 α

-ból

α = 180^{\circ} / 7

, ami ismét nem szerkeszthető;

B C = B D

-ből pedig

α = 36^{\circ}

, ez viszont a szabályos

10

-szög szerkeszthetősége folytán szerkeszthető.
2. Legyen

A D

ellentétes irányú

A C

-vel. Ekkor

B D C ∢ = α / 2

és

C B D ∢ = 3 α / 2 > B D C ∢

, tehát a

B D C

háromszög kétféleképpen lehet egyenlő szárú

B C = B D

-vel, amiből

α / 2 = 180^{\circ} - 2 α

, és így

α = 72^{\circ}

, ami szerkeszthető, ‐ ill.

B D = C D

-vel, amiből

3 α / 2 = 180^{\circ} - 2 α

, és így

a = 360^{\circ} / 7

, nem szerkeszthető.

Arató Péter (Kaposvár, Táncsics M. g. IV. o. t.)

Megjegyzések: 1. A három megszerkeszthetetlen eset ábrái csak abban különböznek, hogy az

A

D

C

betűk ciklikusan permutálódnak.
2. A versenyzők többsége nem tért ki valamennyi lehetőségre.

II. megoldás: Trigonometriai ismeretekre támaszkodva is válaszolhatunk a kérdésre. Lényegében az a kérdés, megszerkeszthető-e az

A B C

háromszög

A C = B C = a

szárából az

A B = c

alap (vagy fordítva), más szóval a

c / a

arányszám, amelynek fele a

B A C ∢ = α

koszinuszát adja.
Vegyük hosszúságegységnek a szárat:

a = 1

, így a háromszög-egyenlőtlenségből

0 < c < 2

, másrészt

cos α = c / 2

. Fejezzük ki a kérdéses

B C D

háromszögnek a szerkesztéssel létrejött oldalait. A

B D = d

szakasz hossza vagy

2 c sin α / 2

, vagy

2 c cos α / 2

aszerint, hogy

A B

-t

A

-tól

C

felé, ill. az ellentétes irányba mértük fel, ugyanis az

A B D

egyenlő szárú háromszög szárai közti szög eszerint lesz

α

, ill.

180^{\circ} - α

. A félszög függvényeit

cos α = c / 2

-vel kifejezve

d^{2} = 2 c^{2} (1 \mp cos α) = c^{2} (2 \mp c)

. Másrészt

C D

hossza

1 - c

, ill.

c - 1

aszerint, hogy

c \leq 1

, ill.

c > 1

vagy pedig

1 + c

. Így a

B C D

egyenlő szárú háromszögben

B D

csak szár lehet, ugyanis a

C D = B C

feltevés

1 \mp c = 1

-gyel

c = 0

-ra, ill.

c - 1 = 1

-gyel

c = 2

-re vezet, és az

A B C

háromszög egyik esetben sem létezik. Aszerint, hogy a másik szár szerepét

B C

játssza-e, vagy

C D

, két esetet kell vizsgálnunk.
1.

B D = B C = 1

, azaz

d^{2} = c^{2} (2 \mp c) = 1

-gyel

c^{3} - 2 c^{2} + 1 = 0

, vagy

c^{3} + 2 c^{2} - 1 = 0

. Könnyű belátni, hogy az első egyenletnek

c = 1

, a másodiknak pedig

c = - 1

gyöke, számunkra azonban egyik sem valóságos megoldás, mert

c = 1

mellett

D

egybeesik

C

-vel, a negatív gyöknek pedig itt nincs értelme. Az egyenletek bal oldalát a megfelelő

c - 1

, ill.

c + 1

gyöktényezővel osztva a további gyökök

c^{2} - c - 1 = 0

, ill.

c^{2} + c - 1 = 0

-ból:

c = (1 \pm \sqrt[]{5}) / 2

, ill.

c = (- 1 \pm \sqrt[]{5}) / 2

. Ezek mint szakaszok megszerkeszthetők, mert a

\sqrt[]{5}

hosszúságú szakaszt az

1

és

2

befogójú derékszögű háromszög átfogójaként kaphatjuk.
A nagyobb gyökök

c = 1, 618 ...

, ill.

c = 0, 618 ...

, velük háromszög szerkeszthető, a megfelelő szögek

α = 36^{\circ}

, ill.

α = 72^{\circ}

; a kisebb gyökök negatívok.
2.

B D = C D

-vel a

C D = \pm (1 - c)

esetekben

c^{2} (2 - c) = 1 - 2 c + c^{2}

-ből

\begin{matrix} c^{3} - c^{2} - 2 c + 1 = 0, \end{matrix}

(1)

C D = 1 + c

esetben pedig

c^{2} (2 + c) = 1 + 2 c + c^{2}

-ből a

\begin{matrix} - c^{3} - c^{2} + 2 c + 1 = 0 \end{matrix}

(2)

egyenletre jutunk. Az utóbbit a

{(- c)}^{3} - {(- c)}^{2} - 2 (- c) + 1 = 0

alakban írva látjuk, hogy gyökei

(- 1)

-szer akkorák, mint

(1)

gyökei^{$^{*}$}, ezért a szerkeszthetőség kérdésében mindkét egyenletnél ugyanarra a válaszra jutunk, így elég (1)-gyel foglalkoznunk.
Mivel (1)-ben valamennyi együttható egész szám és

c^{3}

együtthatója

1

, azért ha van racionális gyöke, az egész szám. Egész gyökként csak az állandó tag osztói:

+ 1

és

- 1

jöhetnek szóba, de egyikük sem gyöke (1)-nek. Így (1) a racionális számtest fölött irreducibilis, egyik gyöke sem szerkeszthető meg.^{$^{*}$}

Szász Domokos (Budapest, Eötvös J. g. IV. o. t.)

Megjegyzés: A 2. esetre kapott válasz után nincs értelme kutatni, van-e egyáltalán olyan egyenlő szárú háromszög,

a = 1

szárral, amelynek

c

alapja eleget tesz (1)-nek, ill. (2)-nek. Mégis az I. megoldás eredményeivel való összeegyeztetés végett megjegyezzük, hogy (1) bal oldalának értéke

\begin{matrix} c = & - 2, 0, 1 / 2, 2 esetén \\ - 7, 1, - 1 / 8, + 1, \end{matrix}

eszerint (1)-nek

- 2

és

0

között,

0

és

1 / 2

között, és

1 / 2

és

2

között van egy-egy gyöke, az utóbbi kettővel létezik egy-egy megfelelő háromszög, a

- 2

és

0

közti gyök

- 1

-szerese pedig (2) révén ad egy háromszöget. Finomabban,

0, 01

lépésekkel haladva kapjuk, hogy (1) pozitív gyökei a

(0, 44;