Kezdőlap


Feladat:	941. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bárczy Pál , Dobos László
Füzet:	1959/október, 51 - 53. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Pont körüli forgatás, Háromszögek nevezetes tételei, Háromszög nevezetes vonalai, A háromszögek nevezetes pontjai, Feladat
Hivatkozás(ok):	Feladatok: 1958/december: 941. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az adott egyeneseket a csúcspontok felhasználása nélkül úgy toljuk el, vagy valamely tengelyre tükrözzük, vagy valamely pont körül elforgatjuk, hogy csúcspont ne jusson csúcspontba. Az új helyzetben megszerkesztjük a nevezetes pontokat és ezeket visszatoljuk, visszatükrözzük, visszaforgatjuk az eredeti háromszögbe. ‐ Ugyanezen elv alapján hasonlósági transzformációval is célhoz juthatunk.

Dobos László (Szeged, Radnóti M. g. II. o. t.)

Megjegyzés. A kívánt nevezetes pontok között egy olyan van, amely egybeeshet egy csúccsal: a magasságpont, éspedig derékszögű háromszögben. Ha tehát a háromszög derékszögű, akkor

M

visszatranszformálása sem hajtható végre. Hogy a háromszögnek

b

és

c

oldalegyenesei derékszöget zárnak be, arról a csúcsok felhasználása nélkül így győződhetünk meg :

b

-nek egy a csúcsoktól különböző pontja körül alkalmas

r

-sugárral olyan kört írunk le, amely

c

-t kétszer metszi, majd a metszéspontok körül is

r

sugarú köröket írunk; ha ezek másodszor is

b

-n metszik egymást, akkor

b

és

c

merőlegesek.

II. megoldás: Legyenek az adott egyenesek

a_{0}

b_{0}

c_{0}

, és jelöljük a velük meghatározott háromszöget

H

-val. Húzzunk

a_{0}

b_{0}

c_{0}

-val mindkét oldalukon ugyanakkora

d

távolságban párhuzamost, legyenek ezek

a_{1}

a_{2}

b_{1}

b_{2}

c_{1}

c_{2}

, az 1-es indexű mindig a ,,belső'' oldalon, vagyis pl.

a_{1}

a_{0}

-nak azon az oldalán, amelyen

b_{0}

és

c_{0}

metszik egymást.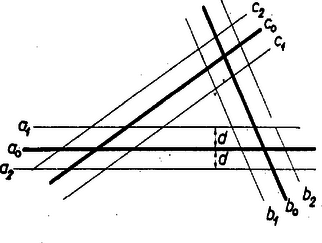

Így számos az eredetivel hasonló helyzetű háromszöget, továbbá paralelogrammákat kaptunk, ezeket fogjuk a szerkesztésekre felhasználni. Az idomokat oldalegyeneseiknek zárójelben való felsorolásával jelöljük, és hasonlóan a metszéspontokat is a megfelelő egyenesekével.
Nyilvánvaló, hogy

H

beírt körének

I

középpontja azonos mind az (

a_{1}

b_{1}

c_{1}

)-be, mind az (

a_{2}

b_{2}

c_{2}

)-be beírt kör középpontjával. Eszerint

I

megszerkeszthető: ha

a_{1}

b_{1}

c_{1}

egy pontban metszik egymást, akkor ez a pont

I

, különben pedig az (

a_{1}

b_{1}

a_{2}

b_{1}

) rombusz (

a_{1}

b_{1}

) (

a_{2}

b_{2}

) átlója adja meg

I

céljára az

a_{0}

és

b_{0}

egyenesek közti belső szög felezőjét. Ugyanígy az előbbi rombusz (

a_{1}

b_{2}

)(

a_{2}

b_{1}

) átlója az

a_{0}

b_{0}

egyenesek külső szögét felezi. Ennek alapján a hozzáírt körök középpontjai is megszerkeszthetők. Egyébként hasonlóan a

H

-nak

a_{0}

oldalához hozzáírt kör

I_{a}

középpontja azonos az (

a_{2}

b_{1}

c_{1}

) és (

a_{1}

b_{2}

c_{2}

) háromszögek

a_{2}

, ill.

a_{1}

oldalához hozzáírt kör középpontjával.
A

H

, (

a_{1}

b_{0}

c_{0}

) és (

a_{2}

b_{0}

c_{0}

) háromszögeknek közös a (

b_{0}

c_{0}

) csúcsukból kiinduló

s_{a}

súlyvonala. Ebből egy‐egy pont az (

a_{1}

b_{0}

)(

a_{2}

c_{0}

) és (

a_{2}

b_{0}

) (

a_{2}

c_{0}

) szakaszok felezőpontja, így

H

-nak

S

súlypontja is megszerkeszthető.
A súlyvonalak kimetszik az adott egyenesekből az oldalfelező pontokat; két ilyenben az oldalfelező merőlegest felállítva megkapjuk

H

körülírt körének középpontját.
Végül

H

-nak pl. (

b_{0}

c_{0}

)-ból húzott

M_{a}

magasságvonala egyben (

a_{1}

b_{0}

C_{0}

)-nak és (

a_{2}

b_{0}

c_{0}

)-nak is magasságvonala. Az utóbbi kettőnek magasságpontja megszerkeszthető mint a

b_{0}

és

c_{0}

oldalra merőleges magasságok metszéspontja, összekötésükben, vagy egyikből az

a_{0}

-ra állított merőlegesben megkapjuk

m_{a}

-t. Végül két magasság metszéspontja megadja

H

-nak

M

magasságpontját.

M

-et az Euler-egyenes alapján is megkaphatjuk az

O S

szakasz

S

-en túli meghosszabbítására rámért 2

O S

szakasz végpontjában.

Bárczy Pál (Hódmezővásárhely, Bethlen G. g. IV. o. t.)

Megjegyzés: A dolgozatok sok különböző szerkesztési eljárást adtak. Itt két olyan megoldást közöltünk, amely egységes kiindulásból valamennyi kívánt pontot előállítja.