Feladat: 940. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bollobás Béla ,  Fekete Jenő ,  Katona Gyula ,  Parti Enikő ,  Szatmári Gábor 
Füzet: 1959/november, 92 - 95. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Trigonometriai azonosságok, Háromszögek nevezetes tételei, Indirekt bizonyítási mód, Feladat
Hivatkozás(ok):Feladatok: 1958/december: 940. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A vizsgálandó összeget tekinthetjük egy olyan mozgó pont útvonala hosszának, amely az A pontból a BC, majd az AC szár egy-egy pontjának útbaejtésével egyenes szakaszokon B-be megy át. ‐ Legyen az ABC háromszögnek a BC, ill. AC szárra való tükörképe A'BC, ill. AB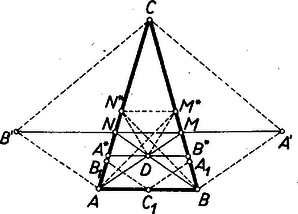'C (1. ábra).

 
 
1. ábra
 
Így AM=A'M és NB=NB', ezért az előírt útvonal minimuma helyett kereshetjük a vele egyenlő A'M+MN+NB' összegnek, vagyis az M és N-re vonatkozó eredeti követelmények mellett az A'-ből B'-be haladó útvonal hosszának minimumát. Az utóbbi kérdés áttekinthetőbb, hiányzik belőle a szárakon való kényszerű irányváltozás. Ha ugyanis C-ből a kétféle útvonalon haladó egy-egy pont felé sugarat irányítunk, ez C körül forog, és forgási iránya az eredeti útvonal esetén kétszer, az M és N-ben való irányváltozáskor ellentétesre fordul, míg a módosított útvonal esetén a forgási irány egyszer sem változik.
Az A' és B' közötti legrövidebb útvonal az A'B' szakasz. Ez meg is felel az előírásnak, hiszen párhuzamos AB-vel, ennélfogva az ACB szög szárai közé eső MN rész-szakaszára is áll; MN∥AB. Valóban, az A'B'C háromszög egyenlő szárú, mert CB'=CB=CA=CA', továbbá szimmetriatengelye, az A'CB' szög felezője, azonos az ABC háromszög szimmetriatengelyével, az ACB szög felezőjével, hiszen az A'CB' szög a BCA szögből úgy keletkezett, hogy mindkét szárán túl ugyanakkora BCA∢=γ szöget adtunk hozzá.
A kérdés csak ez: van-e mindig A'B'-nek a BCA szög szárai közé eső MN szakasza, metszi-e mindig az A'B' szakasz a CB, CA szár-szakaszokat egy-egy belső pontjukban? Ennek szükséges és elegendő feltétele, hogy az A'CB' szög kisebb legyen 180∘-nál, vagyis hogy az ACB szög kisebb legyen 60∘-nál. Ilyenkor az AC=BC szárak nagyobbak az AB-alapnál.
Megmutatjuk, hogy a további esetekben, vagyis ha ACB∢≥60∘ és így A'CB'≥180∘, nincs a követelményeknek megfelelő minimális útvonal. Ugyanis M-et nem választhatjuk a BC szár C végpontjában, mert különben a rajta keresztül AB-vel párhuzamosan húzott egyenes AC-ből N számára is C-t adná. Így azonban az MN egyenes határozatlan, nem mondhatjuk róla, hogy párhuzamos AB-vel. ‐ Ha pedig M a BC szárnak a C-től különböző pontja, és N-et ismét az AB-vel M-en át húzott párhuzamossal metsszük ki AC-ből, akkor az A'MNB' útvonal nem minimális, mert van nála rövidebb, ilyen pl. a CM szakasz M1 pontjával ugyanígy szerkesztett útvonal (2. ábra).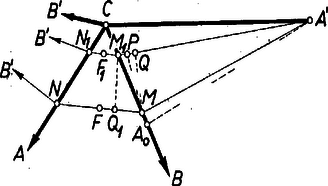
 
 
2. ábra
 
Szimmetria folytán elég ezt az útvonalak felére, az A'M+MF, illetve A'M1+M1F1 összegekre megmutatni, ahol F, F1 az MN, M1N1 szakasz felezőpontja. Ez nyilvánvaló akkor, ha A'CB∢=ACB∢≥90∘, mert ilyenkor A'M1<A'M és M1F1<MF. Ha 90∘>A'CB∢≥60∘, akkor is elég M-ként a CA' szakasz CB-n levő CA0 vetületének pontjaival foglalkozni, amelyekkel A'MC∢≥90∘, és így A'M1>A'M; különben ugyanis M helyett A0 is rövidebb útvonalat ad.
Legyen ilyenkor P az A'M1 szakaszon az a pont, amelyre A'P=A'M, továbbá M vetülete A'M1-re Q, és M1 vetülete MN-re Q1. Ekkor az A'M1 útszakasz többlete A'M-hez képest M1P, és M1F1 hiánya MF-hez képest MQ1, így azt kell megmutatnunk, hogy M1P<MQ1. P nyilván az M1Q szakaszon van, így M1P<M1Q. Másrészt M1Q<MQ1, mert mindkét szakasz MM1-nek vetülete, és az MM1Q hajlásszög, mint az A'CM1 háromszög külső szöge, nagyobb 60∘-nál, az M1MQ1 hajlásszög viszont legfeljebb 60∘, ugyanis pótszöge a BAC szög felének, ami legalább 30∘, és nagyobb (de hegyes) hajlásszög esetén a vetület kisebb. ‐ Ezzel a bizonyítást befejeztük.
 

Fekete Jenő (Mosonmagyaróvár, Kossuth L. g. II. o. t.)
 

Megjegyzések: 1. Lényegében azonos a közölt megoldással a következő szerkesztés: tükrözzük az ABC háromszög CD magasságát BC-re, és bocsássunk erre A-ból merőlegest; ez metszi ki BC-n M-et.
 

Katona Gyula (Budapest, Kandó K. híradásip. t. IV. o. t.)
 

2. Felhasználva, hogy MN∥BA, és hogy A', M, N egy egyenes pontjai, M-et A' és B' megszerkesztése nélkül, a BC szárból az A körül AB sugárral írt körrel is kimetszhetjük. Valóban, A'BM∢=ABM∢=NMC∢=A'MB∢, az A'BM háromszög egyenlő szárú és így AM=A'M=A'B=AB. Ha a minimum létezésének AB<AC feltétele teljesül, akkor egyszersmind AM<AC, tehát M a BC szakaszon van.
 

Parti Enikő (Budapest, Bagi Ilona lg. III. o. t.)
 

3. A legtöbb dolgozat ACB∢≥60∘ esetére M és N mindegyikét C-be helyezve AC+CB-t adja meg minimumnak.
 

II. megoldás: ACB∢<60∘ esetére a minimumhoz a következő meggondolással is eljuthatunk. Tegyük fel, hogy megtaláltuk a minimális AMNB≡U útvonalat adó M pontot. Húzzunk AM és BN-nek D metszéspontján át AB-vel A*B* párhuzamost (1. ábra). D belső pontja a háromszögnek, ezért A* az AC, B* a BC szakaszon van. Megmutatjuk, hogy a DMN háromszög, amely bele van írva az A*B*C háromszögbe, és amelynek kerülete képezi az útvonal középső DMND szakaszát, talpponti háromszöge az A*B*C egyenlő szárú háromszögnek.
D mindenesetre talppontja a C-ből húzott magasságnak, mert benne van az ABMN egyenlő szárú trapéz szimmetria-tengelyében, amely az ABC és A*B*C egyenlő szárú háromszögeknek is tengelye. Ha már most M és N nem volna azonos az A*B*C háromszög A*, B*-ból húzott magassága M*, ill. N* talppontjával, akkor annak az ismert tételnek az alapján, hogy a hegyesszögű háromszögbe beírt háromszögek közül a talpponti háromszög a legkisebb kerületű,* az 5 szakaszból álló ADM*N*DB útvonal rövidebb volna U-nál, mert középső DM*N*D útszakasza rövidebb U-nak DMND középső szakaszánál, kezdő és végszakaszaikban pedig megegyeznek. És még rövidebb volna az AM*N*B útvonal, mert az ADM* háromszögben (amelynek csúcsai M és M* különbözősége folytán nem esnek egy egyenesbe) AM*<AD+DM*, és ugyanígy N*B<N*D+DB. Márpedig az AM*N*B útvonal is megfelel a feladat követelményeinek, mert M* és N* a CB* CA* szakasznak belső pontjai, tehát rajta vannak a BC, AC száron, továbbá M*N*∥A*B*∥AB, mert az A*B*M* és A*B*N* derékszögű háromszögek egybevágók (az átfogó és két szög) így B*M*=A*N*, tehát az N*M*C háromszög is egyenlő szárú. Ellentmondásra jutottunk: az AM*N*B útvonal rövidebb a minimális U-nál, helytelen tehát az a feltevés, hogy M*≢M és N*≢N, vagyis DMN valóban talpponti háromszöge A*B*C-nek.
Mivel pedig az A*B*C háromszög hasonló helyzetű ABC-vel, és így ugyanez áll MND és A1B1C1 talpponti háromszögeikre is, azért ezek alapján a minimális útvonal AM és BN szakaszait úgy szerkesztjük meg, hogy A, B-n át párhuzamost húzunk az ABC háromszög talpponti háromszögének C1A1 ill. C1B1 oldalaival. Ismeretes, hogy A1C1B∢=ACB∢, eszerint M akkor és csak akkor lesz rajta BC-n, ha MAB∢=ACB∢<CAB∢, vagyis ACB∢<60∘.
 

Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.)
 

III. megoldás: Legyen AB=1, CAB∢=α és fejezzük ki az y=AM+MN+NB összeget az M helyzetét meghatározó BMA∢=φ függvényeként. (M akkor és csak akkor van a BC szakaszon, ha egyrészt az ABM háromszögből φ=180∘-MBA∢-BAM∢<180∘-MBA∢=180∘-α, másrészt az ACM háromszögből φ=MAC∢+ACB∢>ACB∢=180∘-2α. Az ABM háromszögből AM=BN=sinα/sinφ, továbbá ennek alapján az AMN háromszögből MN=sin(φ-180∘+2α)/sinφ=-sin(2α+φ)/sinφ és
y=2sinα-sin(2α+φ)sinφ=2sinα-sin2αcosφsinφ-cos2α==2sinα-2sinαcosαcosφsinφ-1+2sin2α.


Ennek a függvénynek φ ugyanazon értéke mellett van a minimuma, mint a következőnek:
y1=y+12sinα=1-cosαcosφ+sinαsinφsinφ=1-cos(φ-α)sinφ,
ugyanis sinα>0. Itt a nevező pozitív, a számláló nem negatív, tehát y1 legkisebb értéke 0, amikor cos(φ-α)=1, φ=α, vagyis az ABM háromszög egyenlő szárú.
Ezzel az értékkel akkor teljesülnek a φ-re tett korlátozások, ha egyrészt α<180∘-α, másrészt α>180∘-2α, vagyis 60∘<α<90∘, amiből ACB∢<60∘.
 

Szatmári Gábor (Budapest, Piarista g. IV. o. t.)

*Lásd pl. Rademacher‐Toeplitz: Számokról és alakzatokról, 23‐31. o. Tankönyvkiadó, 1953. Középiskolai Szakköri Füzetek.