Kezdőlap


Feladat:	934. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	, Dániel Gábor , Szücs Jozsef , Tusnády Gábor
Füzet:	1959/szeptember, 15 - 17. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Vetítések, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1958/november: 934. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A szóban forgó $3$ ‐ $3$ háromszög rendre a $T A B C$ , $T A C D$ , $T A D B$ tetraédernek $1$ ‐ $1$ lapja. E lapokhoz a $3$ tetraéderben ugyanakkora magasság tartozik. Ugyanis a $T B C$ , $T C D$ , $T D B$ lapok a $B C D$ síkban feküsznek, ennélfogva az ezen lapokhoz tartozó $m$ magasság közös: $A$ -nak a $B C D$ síktól való távolsága. Az $A B C$ , $A C D$ , $A D B$ lapokhoz tartozó magasságokat $T$ -nek e lapsíkoktól való $t$ távolsága adja, ami ugyanakkora, mert ez a tulajdonsága $f_{a}$ minden pontjának megvan. Ennek alapján pl. a $T A B C$ tetraéder $3$ -szoros köbtartalma kétféle kifejezésének $T B C \cdot m = A B C$ . $t$ egyenlőségéből (a háromszögek területét ugyanúgy jelöltük, mint magukat a háromszögeket):

\begin{matrix} T B C : A B C = t : m = k, és így T B C = k \cdot A B C . \end{matrix}

(1)

Ugyanez áll a

T C D : A C D

és a

T D B : A D B

arányokra is, ennélfogva valóban

\begin{matrix} T B C : T C D : T D B = A B C : A C D : A D B . \end{matrix}

Szűcs József (Szeged, Ságvári E. gyak. g. III. o. t.)

II. megoldás: Tekintsük a

T

ponton, továbbá az

A

ponton át

B C

-re merőleges

S_{1}

és

S_{2}

síkot.

S_{1}

tartalmazza

T

-nek az

A B C

lapon levő

T_{1}

és a

B C

élen levő

T_{2}

merőleges vetületét,

S_{2}

pedig

A

-nak a

B C D

lapon levő

A_{1}

és a

B C

élen levő

A_{2}

merőleges vetületét. A

T T_{1} T_{2}

és

A A_{1} A_{2}

háromszögek hasonlók, mert

T_{1}

, ill.

A_{1}

-nél derékszögűek, továbbá

T T_{2} T_{1}

és

A A_{2} A_{1}

szögeik egyenlők, mindegyik megadja az

A B C

és

D B C

lapok hajlásszögét. Ennélfogva (a fenti jelölésekkel)

\begin{matrix} T T_{2} : A A_{2} = T T_{1} : A A_{1} = t : m . \end{matrix}

(2)

Innen a bal oldali arány mindkét tagját

B C / 2

-vel szorozva, és a szorzatokban a szóban forgó területek kifejezését felismerve (1)-et kapjuk.
Ha az

A B C

és

D B C

síkok merőlegesek egymásra, akkor az említett derékszögű háromszögek egyenes szakasszá fajulnak ugyan, azonban

T_{1} \equiv T_{2}

és

A_{1} \equiv A_{2}

, ennélfogva (2) érvényes marad. Nem érinti meggondolásunk érvényességét az sem, ha e két sík nem merőleges, és a tetraéder a tompa lapszögben helyezkedik el.

Tusnády Gábor (Sátoraljaújhely, Kossuth L. g. IV. o. t.)

III. megoldás: Vetítsük (merőlegesen) a tetraédert egy az

f_{a}

-ra merőleges

S

síkra, és legyen a szóbanforgó pontok vetülete rendre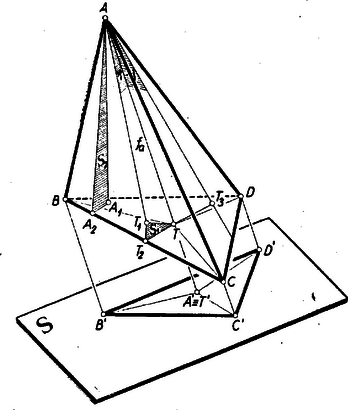

A'

B'

C'

D'

T'

Ekkor

T' \equiv A'

, ennélfogva a vizsgálandó

3

‐

3

háromszög vetületei páronként egybeesnek. Tudjuk, hogy síkidom valamely síkon való merőleges vetületének területe egyenlő az idom területéből és a két sík (nem tompa) hajlásszögének koszinuszából képezett szorzattal. Így ‐

S

-nek a

D B C

, ill.

A B C

lapsíkkal alkotott hegyes szögét

α

, ill.

β

-val jelölve ‐

\begin{matrix} T B C cos α = T' B' C' = A' B' C' = A B C cos β, \end{matrix}

és innen

\begin{matrix} T B C : A B C = cos β : cos α . \end{matrix}

Ugyanez áll a további két háromszögpárra is, mert

S

A C D

A D B

lapsíkokkal is

β

szöget zár be. Valóban, az

A

csúcson átmenő lapsíkok egyenlő

γ

szögeket zárnak be

f_{a}

-val (gondoljunk az

A T T_{1}

A T T_{3}

A T T_{4}

egybevágó derékszögű háromszögekre, ahol

T_{3}

T_{4}

T

-nek

A C D

-n,

A D B

-n levő vetülete),

S

-sel bezárt szögük pedig pótszöge

γ

-nak. Ezzel az állítást bebizonyítottuk.
(Sem

α

, sem

β

nem lehet derékszög. Ha ugyanis

α = 90^{\circ}

volna, akkor ‐

S

-et éppen

T

-n át fektetve ‐ az

S

-re merőleges

f_{a}

-val együtt

A

benne feküdnék

B C D

-ben, tetraéderünk elfajult volna. Ugyanez adódik

β = 90^{\circ}

-ból is, mert így

A'

B'

C'

egy egyenesbe esnek, és hasonlóan

A'

B'

D'

is).

Dániel Gábor (Bp. VIII., Piarista g. IV. o. t.)

Megjegyzések. 1. Ha a tetraéder A csúcsa körüli lapszögek közül

2

külső és

1

belső lapszög felezősíkjainak közös

f_{a}^{*}

metszésvonalát tekintjük, és ennek

B C D

-vel való metszéspontját

T^{*}

-gal jelöljük, akkor a

T^{*} B C

T^{*} C D

T^{*} D B

háromszögek területeinek aránya ugyancsak megegyezik az

A B C

A C D

A D C

lapok területeinek arányával. Meggondolásaink erre az esetre is érvényesek, mert

T^{*}

is egyenlő távolságban van ezen három lap mindegyikétől.
2. Több dolgozat arra a helytelen feltevésre támaszkodott, hogy

T

B C D

háromszög belső szögfelezőinek metszéspontja, vagyis azonos a beírt kör középpontjával. Ez csak akkor igaz, ha

f_{a}

merőleges

B C D

-re.