Kezdőlap


Feladat:	933. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andréka Bertalan , Arató P. , Barabás Gy. , Bárczy Zsolt , Bartha L. , Biborka T. , Bollobás B. , Csanak Gy. , Cséfalvay Klára , Durst I. , Fejes L. , Gaál S. , Grallert F. , Gyene A. , Hadik Z. , Halász Á. , Halász G. , Katona Gy. , Kelle L. , Kisvölcsey J. , Koszterszitz Gy. , Losonczi L. , Máté A. , Máté Zs. , Mihályffy L. , Náray Miklós (Bp.) , Németh Judit , Parti Enkő , Pósch Margit , Soós S. , Szabó Gy. , Szász D. , Szücs J. , Tatai P. , Tihanyi A. , Tusnády G. , Vörös I.
Füzet:	1959/május, 143 - 144. oldal		PDF \| MathML
Témakör(ök):	Körérintési szerkesztések, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1958/november: 933. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az adott szakasz hossza $2 s$ . Az $A B C$ háromszögnek az a külső érintő köre, amely a $B C$ oldalt kívülről érinti, az $A B = e$ , $A C = f$ oldalegyeneseket azokban a $C_{1}$ , $B_{1}$ pontokban érinti, amelyekre $A C_{1}$ és $A B_{1}$ a kerület felével, $s$ -sel egyenlők. Így ez a $k$ kör megszerkeszthető, és a keresett szelő $k$ -nak az a $P$ -n át húzott érintője lesz, amely $A$ -t elválasztja $k$ -tól, másképpen: amely $k$ -t az $A$ -ból ,,látható'', azaz rövidebb $B_{1} C_{1}$ ívén érinti.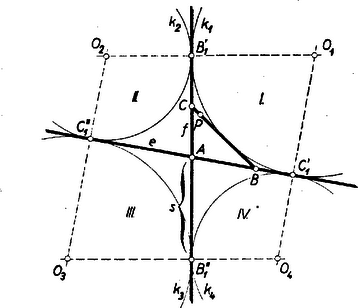
$B_{1}$ és $C_{1}$ két-kétféleképpen tűzhető ki $e$ , $f$ -en, és így a szerkesztést négy $k$ -val folytathatjuk. Nevezzük az $e$ , $f$ -fel négy részre vágott sík részei közül a $P$ -t tartalmazó I-nek, az ebből $f$ , $A$ , ill. $e$ átlépésével elérhetőket rendre II, III, IV-nek; legyenek továbbá az ezekben fekvő körök rendre $k_{1}$ , $k_{2}$ , $k_{3}$ , $k_{4}$ , végül $k_{1}$ és $k_{3}$ érintési pontjai $C'_{1}$ , $B'_{1}$ , ill. $C''_{1}$ , $B''_{1}$ .

1. ábra

Az adott

P

pont

k_{2}

k_{3}

k_{4}

-re nézve biztosan külső pont.

k_{3}

révén mégsem kapunk megoldást, mert

k_{3}

-nak

P

-ből látható íve belső részívként tartalmazta a rövidebb

B''_{1} C''_{1}

ívet.

k_{2}

(és

k_{4}

) mindegyike révén pontosan egy megoldást kapunk, mert

P

-ből

C''_{1}

k_{2}

-n) nem látható,

B'_{1}

látható, tehát

k_{2} P

-ből látható ívének egyik végpontja a rövidebb

C''_{1} B'_{1}

íven van, a másik pedig a hosszabikon. Végül

P

-ből

k_{1}

-hez aszerint húzhatunk

2

1

, vagy

0

megfelelő érintőt, hogy

P

a rövidebb

B'_{1} C'_{1}

ívvel és az

A B'_{1}

A C'_{1}

szakaszokkal határolt síkidomra nézve belső, ill. az íven fekvő, ill. külső pont.
Ezek szerint a megoldások száma

4

3

, vagy

2

Bárczy Zsolt (Hódmezővásárhely, Bethlen g. III. o. t.)

Megjegyzés. Némileg más elemzéssel vezet ugyanerre a szerkesztésre a következő meggondolás. Képzeljük a feladatot megoldottnak és állítsuk elő az

A B C

háromszög kerületét mindhárom oldalegyenesén:

A

-ból egyrészt

e

, másrészt

f

mentén,

B

-n, ill.

C

-n át haladva, legyenek így a végpontok

B_{0}

, ill.

C_{0}

, továbbá a

B A

, ill.

C A

oldalt

B C

-nek

B

-n, ill.

C

-n túli meghosszabbítására rámérve, vagyis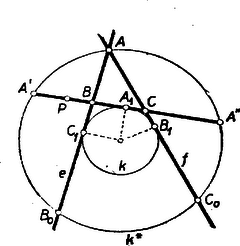

A' B = A B

és

C A'' = C A

-val.

2. ábra

Így

A B_{0} = A C_{0} = A' A'' = 2 s

. Az I. megoldásbeli

k

külső érintő kör e három szakaszt rendre a

C_{1}

B_{1}

A_{1}

felezőpontjukban érinti. Ezt

B_{1}

és

C_{1}

-re már fent láttuk, és az

A_{1}

érintési pont is felezőpont, mert

A' A_{1} = A' B + B A_{1} = A B + B C_{1} = A C_{1} = s

. Eszerint

B_{0}

C_{0}

A

A'

és

A''

egy (a

k

-val közös középpontú)

k^{*}

körön vannak.

k^{*}

-ot az első

3

pont meghatározza, ahhoz kell

P

-n át olyan szelőt szerkeszteni, amely

2 s

hosszúságú húrt metsz ki belőle, és amely

A

-t elválasztja

k^{*}

középpontjától. (Itt kapcsolódunk a fenti megoldáshoz, ugyanis

k^{*}

-ban a

2 s

hosszúságú húrok a középponttól

k

sugarával egyenlő távolságban vannak.)

Andréka Bertalan (Győr, Bencés g. IV. o. t.)