Kezdőlap


Feladat:	932. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barabás György , Csanak György , Gáti Pál , Tomcsányi Gyula
Füzet:	1959/május, 134 - 135. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Körülírt kör, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1958/november: 932. matematika feladat

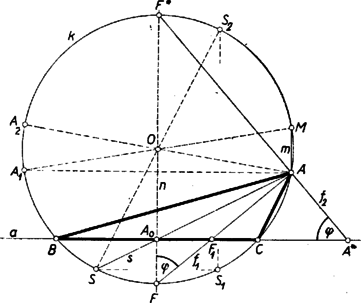
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Vegyük észre feladatunk kapcsolatát a 926. feladattal. Az ott adott elemzések alapján egy szerkesztés a következő (lásd a 926. feladat ábráját): az $A$ -ban $A A^{*} = f_{2}$ -re és $A_{0}$ -ban $A_{0} A^{*} = a$ -ra állított $f_{1}$ , ill. $n$ merőlegesek metszéspontja $F$ ; $A F$ felező merőlegese $n$ -ből kimetszi $O$ -t, végül az $O$ körül $O A = O F$ sugárral írt kör $a$ -ból kimetszi $B$ és $C$ -t.

A lépések egyértelműek, legfeljebb

1

megoldás lehet. Van megoldás, ha

F

a

-nak

A

-val ellentétes partján jön létre. Ennek feltétele, hogy

f_{1}

-nek

a

-n való,

F_{1}

metszéspontja

A_{0}

-nak ugyanazon oldalán legyen, mint

A^{*}

(ne essék egybe

A_{0}

-val), amit úgy is mondhatunk, hogy az

A^{*} A A_{0}

szög nagyobb legyen derékszögnél.
Ha az

A^{*} A A_{0}

szög derékszög (így persze az előbbi feltétel nem áll), akkor azért is megoldhatatlan a feladat, mert az adatokban ellentmondás van, hiszen így a háromszög csak egyenlő szárú lehetne, akkor pedig

A^{*}

nem létezik.

Gáti Pál (Pécs, Nagy Lajos Gimn. II. o. t.)

Megjegyzés:

O

-t

n

-ből

m

-nek

f_{1}

-re (vagy ami ugyanaz,

f_{2}

-re) való tükörképével is kimetszhetjük, mert

f_{1}

és

f_{2}

felezik az

A M

és

A O

egyenesek közti szögeket. Valóban, az

A A_{2}

átmérő végpontjai

M

-mel derékszögű háromszöget alkotnak, így

M A_{2} ∥ B C

, tehát

F

és

F^{*}

M A_{2}

íveknek is felezőpontjai.

Barabás György (Bp. V., Apáczai Csere J. Gyak. Gimn. IV. o. t.)

II. megoldás:

F_{1}

ismeretében

A_{0} B

-t mértani középként is előállíthatjuk, és ennek

A_{0}

-ból

a

-ra való felmérésével megkapjuk

B

-t és

C_{t}

-t. Ugyanis a szögfelezők révén előállott metszetekre

\begin{matrix} B F_{1} : C F_{1} = A B : A C = B A^{*} : C A^{*}, \end{matrix}

azaz,

C A_{0} = B A_{0}

, figyelembe vételével

\begin{matrix} (B A_{0} + A_{0} F_{1}) : (B A_{0} - A_{0} F_{1}) = (A_{0} A^{*} + B A_{0}) : A_{0} A^{*} - B A_{0}), \end{matrix}

és innen

\begin{matrix} B A_{0}^{2} = A_{0} F_{1} \cdot A_{0} A^{*} . \end{matrix}

Csanak György (Debrecen, Fazekas M. Gyak. Gimn. IV. o. t.)

III. megoldás: Legyen

A A^{*} A_{0} ∢ = φ

, Ez és az

A F F^{*}

szög egyenlők, mert merőleges szárú hegyesszögek. Ezért, ha

A

-nak tükörképe

n

-re

A_{1}

, akkor

A A_{1}

-et

F

-ből, ennélfogva

B

és

C

-ből is

2 φ

szögben látjuk. ‐ Eszerint

B

és

C

-t az

A_{0} A^{*}

egyenesből kimetszhetjük azzal a körívvel, amelynek pontjaiból

A A_{1}

látószöge

2 φ

. Egyébként

2 φ = | β - γ |

, a mondott körív pedig része a háromszög körülírt körének.

Tomcsányi Gyula (Bp. I., Toldy F. Gimn. II. o. t.)