Kezdőlap


Feladat:	929. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Biborka Tamás , Gaál Sándor , Gy. Molnár Szabolcs , Pósa Lajos
Füzet:	1959/május, 138 - 140. oldal		PDF \| MathML
Témakör(ök):	Beírt háromszög, Függvényvizsgálat, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1958/november: 929. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Függvényünk $x$ -nek $- 1 \leq x \leq 1$ értékeire van értelmezve, elég azonban a $0 \leq x \leq 1$ értékekre vizsgálni, mert ha egy ilyen $x_{0}$ mellett értéke $y_{0}$ akkor a $- 1 \leq - x_{0} \leq 0$ -nak eleget tevő $- x_{0}$ -ra értéke $- y_{0}$ szokásos elnevezéssel: $y$ páratlan függvény, grafikonjának az origó szimmetria-középpontja). Így ha a függvénynek az $x_{0}$ helyen maximuma van, akkor a $- x_{0}$ helyen minimuma, és megfordítva.
Írjunk $\sqrt[]{1 - x^{2}}$ helyett $z$ -t. Ekkor $x = \sqrt[]{1 - z^{2}}$ , $y = \sqrt[]{1 - z^{2}} (z + 1)$ és amíg $x 0$ -tól $1$ -ig nő, addig $z 1$ -től $0$ -ig fogy, tehát az új függvényt $0 \leq z \leq 1$ -re vizsgáljuk. ‐ Így $y$ sehol sem negatív, tehát ha van maximuma, az ugyanott van, ahol a négyzetének, $y^{2} (1 - z^{2}) = {(z + 1)}^{2} = (1 - z) ({z + 1)}^{3}$ -nek. Hogy alkalmazhassuk a számtani és a mértani közép közötti egyenlőtlenséget, vizsgáljuk ennek $3$ -szorosát, ugyanis $3 y^{2} = (3 - 3 z) (z + 1) (z + 1) (z + 1)$ -ben a tényezők összege, és így számtani közepe is állandó: $3 / 2$ . Ezt az értéket a tényezők mértani közepe is eléri, tehát van maximuma, éspedig akkor, ha $3 - 3 z = z + 1$ , azaz $z = 1 / 2$ . Ez a $z$ érték benne van a vizsgált intervallumban, vele az $x = \sqrt[]{3} / 2$ helyen $3 y^{2}$ maximuma ${(3 / 2)}^{4}$ , tehát $y$ maximuma $3 \sqrt[]{3} / 4$ .
Ezek és az előzetes megjegyzés szerint $y$ -nak minimuma is van: $x = - \sqrt[]{3} / 2$ -nél $y = - 3 \sqrt[]{3} / 4$ .

Gy. Molnár Szabolcs (Kisújszállás, Móricz Zs. Gimn. III. o. t.)

II. megoldás: Célszerű az

x = sin t

helyettesítés is, evvel

\sqrt[]{1 - x^{2}} = | cos t |

függvény. A

sin t

periodikus volta folytán végtelen sok olyan intervallum van

t

-re, melyen végig futva

x

-nek minden értékét pontosan egyszer kapjuk meg. Célszerű a

- π / 2 \leq t \leq π / 2

intervallum, ekkor

cos t \geq 0

, és így

y = sin t (cos t + 1) = sin t + 0, 5 sin 2 t

Most már

y

pozitív értékei közül a maximum keresése speciális esete a 826. feladatban vizsgált kérdésnek¹:

A = 1

B = 0, 5

-del. Ezekkel az ott kapott képlet szerint

{(cos t)}_{1} = - 1

, ez számunkra kizárt érték,

{(cos t_{1})}_{2} = 1 / 2

pedig

{(sin t)}_{2} = x = \sqrt[]{3} / 2

-re vezet.

Gaál Sándor (Veszprém, Lovassy L. Gimn. IV. o. t.)

III. megoldás: Nemnegatív

x

-ekre geometriai értelmezést tulajdoníthatunk kérdésünknek.

z = \sqrt[]{1 - x^{2}} + 1

azt a

P Q

ordinátát adja meg, amely a derékszögű koordinátarendszerben a

(0,1)

pont körül

r = 1

sugárral írt

k

körön, ennek az

y = 1

egyenes fölötti félkörén fekvő,

x

abszcisszájú

P

ponthoz tartozik.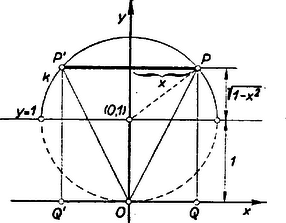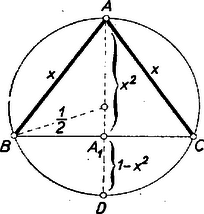

1. ábra

x \geq 0

P

tükörképe az

Y

tengelyre

P'

, és vetületeik az

X

tengelyen

Q

, ill.

Q'

; akkor a vizsgálandó

y = x z

függvény a

Q P P' Q'

téglalap területét adja meg, ami kétszerese a

k

-ba írt

O P P'

egyenlő szárú háromszög területének. Ebben az értelmezésben feladatunk megkeresni az egységkörbe írt egyenlő szárú, nem tompaszögű háromszögek közül a legnagyobb területűt ‐ ha ilyen egyáltalán van. Ismeretes, hogy ilyen van: az egyenlő oldalú háromszög.²

2. ábra

Ennek oldala

P P' = 2 x = \sqrt[]{3}

, így a maximum helyeként ismét

x = \sqrt[]{3 / 2}

-re jutottunk.

Pósa Lajos (Bp. XIII., Sziget utcai ált. isk. V. o. t.)

IV. megoldás: Más jellegű geometriai értelmezése

y

-nak: az

A D = 1

átmérőjű körbe írt

A B C

háromszög kerületének fele, ha

A B = A C = x

. Ha ugyanis

A B

felező pontja

A_{1}

, akkor az

A D B

, ill.

A B A_{1}

derékszögű háromszögből

A A_{1} \cdot A D = A A_{1} = A B^{2} = x^{2}

, és így

B A_{1}^{2} = A A_{1} \cdot A_{1} D = x^{2} (1 - x^{2})

, tehát a félkerület:

A_{1} B + B A = x \sqrt[]{1 - x^{2}} + x = y

. Eszerint feladatunk meghatározni az egységnyi átmérőjű körbe írt, egyenlő szárú háromszögek közül a legnagyobb kerületűt, ha ilyen egyáltalán van. Ismeretes, hogy ilyen van: az egyenlő oldalú háromszög,³ ennek oldala

x = \sqrt[]{3} / 2

Biborka Tamás (Makó, József A. Gimn. II. o. t.)

Megjegyzés.Több a III., ill. a IV. megoldáshoz hasonló dolgozat így következtetett: ,,Minden egyenlő szárú, nem egyenlő oldalú

H_{1}

háromszög helyett lehet venni ugyanazon körbe írt, egyenlő szárú, nagyobb területű, kerületű

H_{2}

háromszöget, ilyen a

H_{1}

szárára, mint alapra a körbe szerkesztett hegyesszögű, egyenlő szárú háromszög. Más szóval:

H_{1}

területe, kerülete növelhető, ,,javítható''. Ugyanez az eljárás az

E

egyenlő oldalú háromszöget önmagával pótolja, ennélfogva

E

területe, kerülete nem javítható. Ezért

E

területe, kerülete maximális.''
Ez a gondolatmenet azért nem helyes, mert

H_{2}

nem egyenlő oldalú, tehát

H_{1}

-et nem

E

-hez hasonlítja. A növelés lehetősége vagy lehetetlensége magában nem biztosítja maximum létezését.⁴

¹Megoldását lásd KML. XVI. kötet, 17. o. (1958 január).

²Lásd pl. Rademacher ‐ Toeplitz: Számokról és alakzatokról, Tankönyvkiadó, 1953, 14 -17., o. (Középiskolai Szakköri Füzetek.) Az idézett helyen annak bizonyítása olvasható, hogy egy adott körbe írható összes háromszögek (konvex $n$ -szögek) közül a szabályosnak van legnagyobb területe.

³Lásd p1. Kürschák-Hajós-Neakomm-Surányi: Matematikai Versenytételek I. rész, Tankönyvkiadó, 1955, 46‐48. o. (Középiskolai Szakköri Füzetek.) Arról az általánosabb tételről van ott szó, hegy egy adott körbeírható összes háromszögek közül az egyenlő oldalúnak van legnagyobb kerülete.

⁴Lásd a 2 alatt idézett műnek ,,Alapvető dolgok maximum feladatokról'' c. fejezetét 127‐135. o.