Kezdőlap


Feladat:	927. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bollobás Béla , Cséfalvay Klára , Klimó János , Mondik László
Füzet:	1959/május, 135 - 138. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Tengelyes tükrözés, Pont körüli forgatás, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1958/október: 927. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. A beérkezett dolgozatok legnagyobb része trigonometriai úton bizonyítja az állítást. Közlünk egy ilyet, majd a II. és III. megoldásokon bemutatjuk, hogy elemi úton is célhoz juthatunk. Elemi utat a dolgozatoknak csak csekély hányadrésze követett.

I. megoldás: Vegyük hosszegységnek a körülírt kör átmérőjét, legyen továbbá

B A_{1}

látószöge a nagyobb

B A_{1}

ív pontjaiból

x

. Ekkor

B A_{5}

látószöge a nagyobb

B A_{5}

ív pontjaiból

36^{\circ} - x

, továbbá

B A_{1} = sin x,

B A_{3} = sin B A_{5} A_{3} ∢ = sin (72^{\circ} + x)

B A_{5} = sin (36^{\circ} - x) = sin (144^{\circ} + x)

B A_{2} = sin B A_{5} A_{2} ∢ = sin (36^{\circ} + x) = - sin (216^{\circ} + x)

B A_{4} = sin B A_{5} A_{4} ∢ = sin (108^{\circ} + x) = - sin (288^{\circ} + x)

.
Ezekkel a bal és jobb oldal különbsége

\begin{matrix} B A_{1} + B A_{3} + B A_{5} - B A_{2} - B A_{4} = sin x + sin (72^{\circ} + x) + sin (144^{\circ} + x) + \\ + sin (216^{\circ} + x) + sin (288^{\circ} + x) = (1 + cos 72^{\circ} + cos 144^{\circ} + cos 216^{\circ} + \\ + cos 288^{\circ}) sin x + (sin 72^{\circ} + sin 144^{\circ} + sin 216^{\circ} + sin 288^{\circ}) cos x . \end{matrix}

Felismerve, hogy a zárójelekben az egymás utáni szögek

72^{\circ}

-nak egymás utáni többszörösei, a különbség értéke ismert általános azonosságok alapján folytatólag:¹

\begin{matrix} (\frac{1}{2} + \frac{sin 324^{\circ}}{2 sin 36^{\circ}}) sin x + \frac{sin 180^{\circ} \cdot sin 144^{\circ}}{sin 36^{\circ}} cos x = 0. \end{matrix}

Ezzel a bal és jobb oldal egyenlőségét bebizonyítottuk.

Klimó János (Kaposvár, Közgazd. Techn.. III. o. t.)

II. megoldás: A

B

pont helyzetének megválasztása folytán mindkét

B A_{3}

ívhez tartozó középponti szög (röviden: a

B A_{3}

ív) nagyobb

144^{\circ}

-nál, az

A_{5}

-öt tartalmazó

B A_{4}

ív kisebb

144^{\circ}

-nál, így a megfelelő húrokra is áll

B A_{3} > B A_{4}

. Ugyanígy

B A_{2}

nagyobb

B A_{1}

és

B A_{5}

mindegyikénél. Így

B A_{4}

-et

B A_{3}

-ra

B

-ből,

B A_{1}

-et

B A_{2}

-re

B

-ből és

B A_{5}

-öt

A_{2} B

-re

A_{2}

-ből rámérve az

A'_{4}

, ill.

A'_{1}

és

A'_{5}

végpontok a

B A_{3}

, ill.

B A_{2}

szakaszon vannak. Húzzuk meg az

A_{4} A'_{4}

A_{1} A'_{1}

A_{1} A'_{5}

szakaszokat (1. ábra).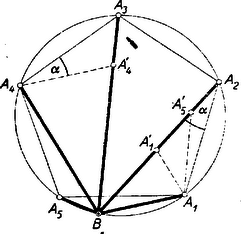

1. ábra

A'_{4} A_{4} B

és

A' A_{1} B

egyenlő szárú háromszögekben

A'_{1} B A_{4} ∢ = A_{3} B A_{4} ∢ = A_{2} B A_{1} ∢ = A'_{1} B A_{1} = 36^{\circ}

, ezért

A'_{4} A_{4} B ∢ = A_{4} A'_{4} B ∢ = A_{1} A'_{1} B ∢ = 72^{\circ}

. Az

A_{1} A_{2} A'_{1}

, ill.

A_{3} A_{4} A'_{4}

háromszögekben az ötszög

A_{1} A_{2} = A_{3} A_{4}

oldalaival szemben

108^{\circ}

-os szögek fekszenek, mert ezek az utóbbi két szögnek mellékszögei. Másrészt

B A_{2} A_{1} ∢ = α

jelöléssel

A_{5} A_{4} B ∢ = A_{5} A_{2} B ∢ = A_{5} A_{2} A_{1} ∢ - B A_{2} A_{1} ∢ = 36^{\circ} - α

, ezért

A'_{4} A_{4} A_{3} ∢ = A_{5} A_{4} A_{3} ∢ - A_{5} A_{4} B ∢ - B A_{4} A'_{4} ∢ = 108^{\circ} - (36^{\circ} - α) - 72^{\circ} = α

. Így az

A'_{1} A_{1} A_{2}

és

A'_{4} A_{3} A_{4}

háromszögek egybevágók, tehát

A'_{1} A_{1} = A'_{4} A_{3}

.
Egybevágók a

A_{1} A_{2} A'_{5}

és

A_{1} A_{5} B

háromszögek is, mert

A_{2}

, ill.

A_{5}

csúcsuknál fekvő szögük és az azt bezáró oldalaik egyenlők, ezért

A_{1} A'_{5}; A_{2} ∢ = A_{1} B A_{5} 2 ∢ = 144^{\circ}

. Ez a szög nagyobb

A_{1} A'_{1} A_{2} ∢ = 108^{\circ}

-nál, ennélfogva

A'_{5}

A'_{1} A_{2}

szakaszon fekszik.
Most már az

A_{1} A'_{5} A'_{1}

háromszögben

A_{1} A'_{5} A'_{1} ∢ = A'_{5} A_{1} A'_{1} ∢ = 36^{\circ}

, tehát

A'_{1} A'_{5} = A'_{1} A_{1} = A'_{4} A_{3}

.
Mindezek alapján:

\begin{matrix} B A_{2} = B A'_{1} + A'_{1} A'_{5} + A'_{5} A_{2} = B A_{1} + A'_{4} A_{3} + B A_{5} = \\ = B A_{1} + B A_{3} - B A_{4} + B A_{5}, \end{matrix}

amiből a bizonyítandó állítás átrendezéssel adódik.

Mondik László (Hódmezővásárhely, Bethlen Gimn. IV. o. t.)

III. megoldás: Legyen az

A_{1} A_{2} A_{3} A_{4} A_{5}

ötszög (röviden

P_{a}

) tükörképe az

A_{5} B

húr

f

felező merőlegesére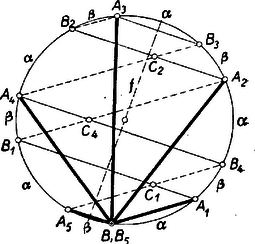

B_{1} B_{2} B_{3} B_{4} B_{5}

(röviden

P_{b}

), ahol

B_{5} \equiv B

(2. ábra).

2. ábra

P_{b}

csúcsai a

P_{a}

köré írt

k

körön vannak, mert

f

k

-nak átmérője.

P_{a}

és

P_{b}

szabályos voltuk folytán egymásba

k

középpontja körül való forgatással is átvihetők, pl.

A_{1}, A_{2}, ..., A_{5}

egy

72^{\circ}

-nál kisebb forgatással átvihetők

B_{4}

B_{3}

B_{2}

B_{5}

-be, ez utóbbi csúcsok

k

-n rendre a rövidebb

A_{1} A_{2}, A_{2} A_{3}, ..., A_{5} A_{1}

ívre esnek. Így a rövidebb

A_{5} B_{5}, B_{5} A_{1}, A_{1} B_{4}, B_{4} A_{2}, ..., A_{4} B_{1}, B_{1} A_{5}

ívek váltakozva egyenlők, legyen röviden

\hat{B_{5} A_{1}} = \hat{B_{4} A_{2}} = ... = \hat{B_{1} A_{5}} = α

és

\hat{A_{5} B_{5}} = \hat{A_{1} B_{4}} = ... = \hat{A_{4} B_{1}} = β

. A

P_{a}

és

P_{b}

oldalai által

k

-ból lemetszett (rövidebb) ívek mindegyike egyenlő a

α + β = 72^{\circ}

-kal.

k

-nak az

f

-re merőleges és így egymással párhuzamos

A_{1} B_{1},

A_{2} B_{2}

A_{3} B_{3}

A_{4} B_{4}

húrjai rendre egyenlők a bizonyítandó egyenlőségben szereplő

B A_{2}

B A_{4}

B A_{1}

B A_{3}

húrokkal, mert a megfelelő húrok végpontjai közé eső rövidebb ív hossza rendre

2 α + β

2 β + α

α

és

3 α + 2 β

vagy

2 α + 3 β

(aszerint, hogy

α \leq β

, ill.

α > β)

. Eszerint elegendő azt megmutatnunk, hogy

\begin{matrix} A_{3} B_{3} + A_{4} B_{4} + A_{5} B_{5} = A_{1} B_{1} + A_{2} B_{2} . \end{matrix}

A_{2} B_{1}

A_{3} B_{2}

A_{4} B_{3}

A_{5} B_{4}

és

A_{1} B_{5}

húrok ugyancsak párhuzamosak, mert két-két egymás utáni húr között két-két

α + β

α

α + β

β

hosszúságú ív van. Ezért,

A_{1} B_{1}

A_{2} B_{2}

A_{4} B_{4}

-nek

A_{5} B_{4}

A_{4} B_{3}

A_{2} B_{1}

-gyel való metszéspontját

C_{1}

C_{2}

C_{4}

-gyel jelölve az

A_{5} B_{5} A_{1} C_{1}

B_{1} C_{1} B_{4} C_{4}

A_{4} C_{4} A_{2} C_{2}

B_{2} C_{2} B_{3} A_{3}

négyszögek paralelogrammák. Ennélfogva

\begin{matrix} A_{3} B_{2} + A_{4} B_{4} + A_{5} B_{5} = B_{2} C_{2} + A_{4} C_{4} + C_{4} B_{4} + C_{1} A_{1} = B_{2} C_{2} + C_{2} A_{2} + B_{1} C_{1} + C_{1} A_{1} = B_{2} A_{2} + B_{1} A_{1}, \end{matrix}

amit bizonyítani akartunk.

Megjegyzés. A használt gondolatmenettel bármely páratlan oldalszámú szabályos sokszögre bizonyítható. A fent bebizonyított tétel következő általánosítása: ha az

A_{1} A_{2} ... A_{2 n + 1}

szabályos sokszög

(n \geq 1)

köré írt kör kisebbik

A_{1} A_{2 n + 1}

ívének valamely pontja

B

, akkor

\begin{matrix} B A_{1} + B A_{3} + B A_{5} ... + B A_{2 n + 1} = B A_{2} + B A_{4} + ... + B A_{2 n} . \end{matrix}

(1)

(Hogy páros oldalszámú sokszögre a gondolatmenet nem használható, ez azon múlik, hogy ekkor az

A_{1} A_{2} ... A_{2 n}

sokszög és ebből az

A_{2 n} B \equiv A_{2 n} B_{2 n}

húrnak

f

felező merőlegesére való tükrözéssel előálló

B_{1} B_{2} ... B_{2 n}

sokszög

4 n

csúcsából álló alakzat a kör középpontjára is tükrös (mert mindkét

2 n

-szög tükrös a középpontra), ezért az

A_{2 n} B_{2 n} = β

ívvel szemben fekvő

A_{n} B_{n}

ív hossza ugyancsak

β

(páratlan oldalszám esetén viszont, mint könnyen belátható, az

{\hat{A_{2 n + 1} B}}_{2 n + 1} = β

-val szemben

{\hat{A_{n + 1} B}}_{n + 1} = α

fekszik). Ezért minden az

A_{2 n} B_{2 n}

-nel párhuzamos

A_{k} B_{k}

húr végpontjai között mindkét

A_{k} B_{k}

íven a

β

ívek száma páratlan, és így ezen húrok rendszerében általában nincs az (1) hal oldalán álló húrokkal egyenlő. Ugyanis a kört az (1) bal oldalán álló húrok bármelyikével kettévágva mindkét íven páros számú

β

ív van. ‐

2 n

oldalú szabályos sokszögre nem is igaz az (1)-nek megfelelő állítás.)
A fenti általánosítást kimondta és a Ptolemaios-tétel felhasználásával be is bizonyította Bollobás Béla (Bp. V., Apáczai Csere J. Gyak. Gimn. II. o. t.). A dolgozatok kisebb része magát az eredeti állítást is így bizonyította. Egy ilyen a következő.

IV. megoldás: Válasszuk hosszúságegységnek az ötszög oldalát és legyen átlóinak közös hossza

d

. Ha

B

A_{1} A_{5}

ív valamelyik végpontja, akkor a bizonyítandó egyenlőség fennáll, mert mindkét kifejezés értéke

1 + d

.
Ha

B

az ív belső pontja (1. ábra), akkor a

B A_{3}

B A_{2}

B A_{4}

húrokat kifejezhetjük

B A_{1}

B A_{5}

és

d

-vel úgy, hogy

A_{1}

B

A_{5}

-höz negyedik csúcsnak rendre

A_{3}

-at,

A_{2}

-t,

A_{4}

-et vesszük és felírjuk e négyszögekre Ptolemaios tételét:

\begin{matrix} B A_{3} = d \cdot B A_{1} + d \cdot B A_{5}, B A_{2} = d \cdot B A_{1} + B A_{5}, B A_{4} = B A_{1} + d \cdot B A_{5} . \end{matrix}

Ezeket a bal, ill. jobb oldalon behelyettesítve mindkét oldalon

(1 + d) (B A_{1} + B A_{5})

áll. ‐ Ezzel a bizonyítást befejeztük.

Cséfalvay Klára (Bp. XIV., Teleki Blanka lg. IV. o. t.)

¹Lásd pl. Faragó László: Matematikai Szakköri Feladatgyűjtemény, 2. kiad. (1955) 52. o. (Középiskolai Szakköri Füzetek.)