Kezdőlap


Feladat:	925. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Losonczi László , Tatai Péter
Füzet:	1959/május, 131 - 133. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Másodfokú (és arra visszavezethető) egyenletek, Harmadfokú (és arra visszavezethető) egyenletek, Súlyvonal, Magasságvonal, Szögfelező egyenes, Körülírt kör, Feladat
Hivatkozás(ok):	Feladatok: 1958/október: 925. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A háromszögről nincs lineáris (szakasz-) adatunk, ennélfogva valamely szakaszát választhatjuk hosszúság egységnek. Legyen ez a szár: $A C = B C = 1$ . Így elegendő az $A B = c$ alapot meghatároznunk. Erre a háromszög egyenlőtlenségből: 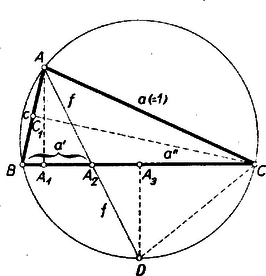$0 < c < 2$ .

Hogy a felezett

A_{1} A_{3}

szakasz két részét kifejezhessük, írjuk fel

A_{1}

A_{2}

A_{3}

-nak

B

-től való távolságát. Ezekből a részek hosszát kivonással képezhetjük, mert

A_{1}

ugyanúgy

B

és

C

között van, mint

A_{2}

és

A_{3}

, hiszen egyenlő szárú háromszög alapján, így

B

-nél hegyes szög van. Pontjaink sorrendje a

B C

oldalon kétféle lehet: vagy

B

A_{1}

A_{2}

A_{3}

C

, vagy

B

A_{3}

A_{2}

A_{1}

C

. Mindkét lehetőség mellett a felezési tulajdonságot a

\begin{matrix} B A_{2} - B A_{1} = B A_{3} - B A_{2} \end{matrix}

(1)

egyenlőség fejezi ki. Legyen a

C

-ből kiinduló magasság talppontja

C_{1}

, így feltevésnél fogva

A C_{1} = c / 2

, A közös hegyes szöggel bíró

B A_{1} A

és

B C_{1} C

derékszögű háromszögek hasonlóságából

\begin{matrix} B A_{1} : B A = B C_{1} : B C, és így B A_{1} = \frac{B A \cdot B C_{1}}{B C} = \frac{c^{2}}{2} . \end{matrix}

A A_{2}

szögfelező által a

B C

oldalon létrehozott szakaszok

B A_{2} : A_{2} C = B A : A C = c : 1

arányából átalakítással

B A_{2} : (B A_{2} + A_{2} C) = c : (c + 1)

, innen

B A_{2} c / (c + 1)

. ‐ Végül

B A_{3} = 1 / 2

.
(1)-ből:

\begin{matrix} 2 B A_{2} = B A_{1} + B A_{3}, \end{matrix}

és fenti kifejezéseinkkel, majd szokásos rendezéssel

(c \neq - 1)

\begin{matrix} \frac{2 c}{c + 1} = \frac{c^{2}}{2} + \frac{1}{2}, \\ c^{3} + c^{2} - 3 c + 1 = 0. & (2) \end{matrix}

Vegyük észre, hogy itt az együtthatók összege

1 + 1 - 3 + 1 = 0

; eszerint

c = 1

gyöke (2)-nek. Ezt azonban mellőzhetjük, mert Így a háromszög egyenlő oldalú,

A_{1}

A_{2}

A_{3}

egybeesnek, ami lényegében elfajult megoldása kérdésünknek.
(2) bal oldalát a

c - 1

gyöktényezővel osztva a

\begin{matrix} c^{2} + 2 c - 1 = 0 \end{matrix}

egyenlet negatív gyöke nem felel meg feladatunk geometriai tartalmának, így

c = - 1 + \sqrt[]{2}

. Ekkor a háromszög

A B

alapján levő szögek nagysága

78^{\circ} 3'

, a szárak közti szög pedig

23^{\circ} 54'

Losonczi László (Miskolc, Gábor Á. Kohóip. t. IV. o.t.)

II. megoldás: A háromszög alapjának és szárának arányát a szögfelező hosszáról a 698. feladatban bebizonyított tétel¹ felhasználásával is megállapíthatjuk. Legyenek a háromszög oldalai:

A C = B C = a

A B = c

, továbbá

B A_{2} = a'

A_{2} C = a''

A A_{2} = f

. Ekkor az idézett tétel szerint

\begin{matrix} f^{2} = a c - a' a'' . \end{matrix}

(3)

Ismeretes továbbá, hogy az

A A_{2}

szögfelező átmegy a háromszög köré írt kör azon

B C

ívének

D

felezőpontján, amely az

A

csúcsot nem tartalmazza. A felezés folytán

D A_{3} ⊥ B C

, így az

A_{2} A_{1} A

és

A_{2} A_{3} D

háromszögek derékszögűek és egybevágók, ugyanis

A_{1} A_{2} = A_{2} A_{3}

és az

A_{2}

-nél levő szögek egyenlők, mert csúcsszögek, ennélfogva

D A_{2} = A A_{2} = f

. Ennek felhasználásával a

B A A_{2}

és

D C A_{2}

háromszögek hasonlóságából (ugyanis szögeik egyenlők)

B A_{2} : A A_{2} = D A_{2} : C A_{2}

, és így

\begin{matrix} f^{2} = D A_{2} \cdot A A_{2} = B A_{2} \cdot A_{2} = a' a'' . \end{matrix}

(4)

(3) és (4)-ből

\begin{matrix} 2 a' a'' = a c . \end{matrix}

(5)

Másrészt a szögfelezőre ismert tétel szerint:

\begin{matrix} \frac{a'}{a''} = \frac{c}{a} . \end{matrix}

(6)

Így (5) és (6)-ból

\begin{matrix} a' = \frac{c}{\sqrt[]{2}}, a'' = \frac{a}{\sqrt[]{2}} . \end{matrix}

Végül az egyenlőszárúság alapján,

a' + a'' = a

felhasználásával

\begin{matrix} \frac{c + a}{\sqrt[]{2}} = a, és így c = (\sqrt[]{2} - 1) a . \end{matrix}

Ez az eredmény megfelel a fentinek.

Tatai Péter (Bp. XIV. ker., I. István Gimn. IV. o. t.)

¹Minden

A B C

háromszögben az

A A_{2}

szögfelezőre

A A_{2}^{2} = A B \cdot A C - B A_{2} \cdot C A_{2}

(KML. XII. kötet 78. o., 1956 március).